In an acute angle triangle ABC, AD, BE and CF are the altitudes, then EFa+FDb+DEc is equal to -Solution in Tamil
FEa+FDb+DEc=acosAa+bcosBb+ccosCa
=cosA+cosB+cosC
≤32
Topper's Solved these Questions
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.10
8 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.11
4 Videos
- PROPERTIES AND SOLUTIONS OF TRIANGLEBOOK - CENGAGECHAPTER - PROPERTIES AND SOLUTIONS OF TRIANGLEEXERCISE - Exercise 5.8
7 Videos
- PROGRESSION AND SERIESBOOK - CENGAGECHAPTER - PROGRESSION AND SERIESEXERCISE - ARCHIVES (MATRIX MATCH TYPE )
1 Videos
- PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEBOOK - CENGAGECHAPTER - PROPERTIES OF TRIANGLE, HEIGHT AND DISTANCEEXERCISE - Question Bank
15 Videos
Similar Questions
In ΔABC, if r1<r2<r3, then find the order of lengths of the sides
View SolutionRegular pentagons are inscribed in two circles of radius 5and 2 units respectively. The ratio of their areas is
View SolutionIf the incircle of the triangle ABC passes through its circumcenter, then find the value of 4sin.A2sin.B2sin.C2
View SolutionIt is given that in a group of 4 students, the probability of 2 students not having the same birthday is 0.893. What is the probability that the 2 students have the same birthday?
View SolutionThe area of a right triangle is 6864 sq. units. If the ratio of its legs is 143:24, then the value of r is ______
View SolutionIn given figure the altitudes AD, BE and CF , the altitudes of triangle ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionAD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionAD, BE and CF, the altitudes of ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionIn an acute angle triangle ABC,AD,BE and CF are the altitudes,then (EF)/(a)+(FD)/(b)+(DE)/(c) is equal to -
View SolutionIn an acute angled triangle ABC, let AD,BE and CF be the perpendicular opposite sides of the triangle. The ratio of the product of the side lengths of the triangles DEF and ABC, is equal to
View SolutionDelta DEF The points between EF, FD and DE are A, B and C, respectively Delta DEF The area of 14.4 cm, which Delta ABC What is the area of?
View SolutionAD, BE and CF , the altitudes of triangle ABC are equal. Prove that ABC is an equilateral triangle.
View SolutionAD, BE and CF are altitudes of △ ABC. If AD = BE = CF, prove that △ ABC is an equilateral triangle.
View SolutionIn ΔABC and ΔDEF , AB = DE, AB∣∣DE, BC = EF and BC∣∣EF. Vertices A, B and C are joined to vertices D, E and F respectively (See fig.)
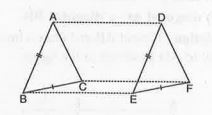 Show that AD∣∣CF and AD=CF.
Show that AD∣∣CF and AD=CF.
View SolutionIf AD, BE, CF are the altitudes of ΔABC whose orthocentre is H, then C is the orthocentre of :
View Solution
