Let ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to Solution in Bengali
3
2
1
0
The correct Answer is:D
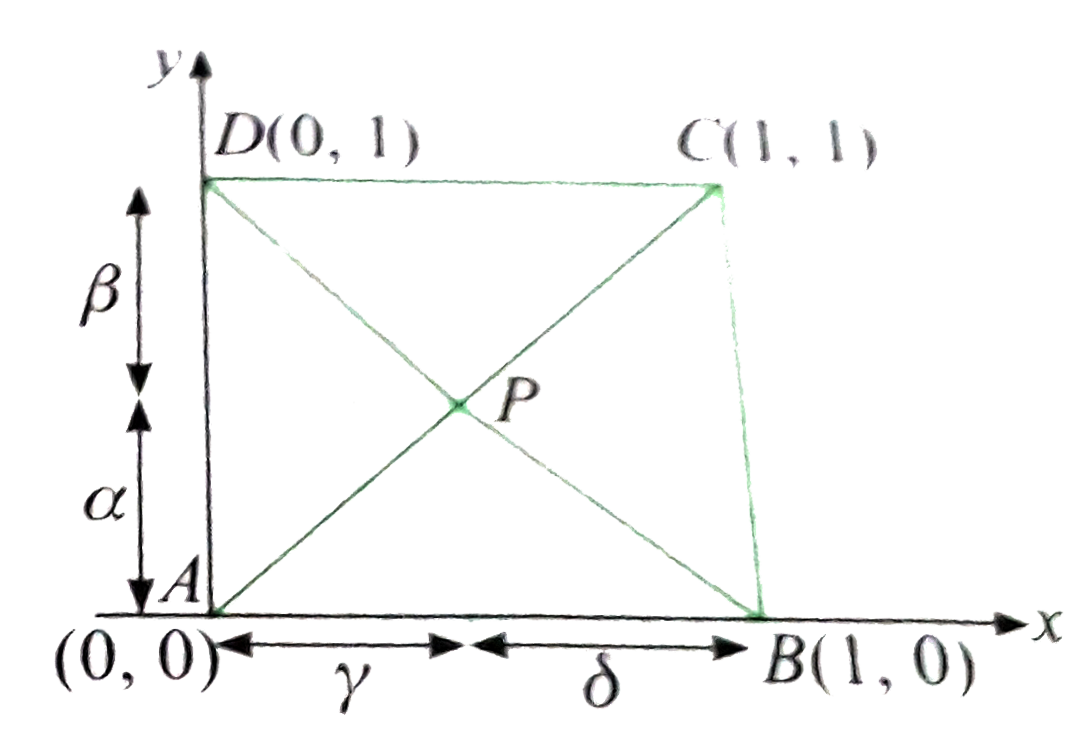
(PA)2−(PB)2+(PC)2−(PD)2
=(α2+γ2)−(α2+δ2)+(δ2+β2)−(γ2+β2)=0
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Matrix match type
4 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Numerical value
12 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
Consider the lines represented by equation (x2+xy−x)×(x−y)=0 forming a triangle. Then match the following lists:

View SolutionLine AB passes through point (2,3) and intersects the positive x and y-axes at A(a,0) and B(0,b) respectively. If the area of ΔAOB is 11. then the value of 4b2+9a2 is
View SolutionIf (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then remaining vertex cannot be
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionLet ABCD is a square with sides of unit length. Points E and F are taken om sides AB and AD respectively so that AE=AF .Let P be a point inside the square ABCD.The maximum possible area of quadrilateral CDFE is-
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is
View SolutionP is an interior point of square ABCD. Prove that PA+PB+PC+PD>2AB.
View SolutionIf P be any point in the plane of square ABCD, prove that
PA2+PC2=PB2+PD2
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The maximum area of quandrilateral CDFE will be -
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to -
View SolutionLet ABCD is a square with sides of unit lenghts . Points E and F are taken on sides AB and AD respectively so that AE =AF . Let P be a point inside the square ABCD. Let a line passing throught point A divides the square ABCD into two parts so that area of one part is double to another , then lenght of the line segment inside the square is -
View SolutionABCD একটি 1 একক বাহুবিশিষ্ট বর্গক্ষেত্র। AB এবং AD- এর ওপর E এবং F বিন্দু দুটি এমনভাবে নেওয়া হল যেখানে AE=AF হয়। মনে করো ABCD বর্গক্ষেত্রের ভিতরে P একটি বিন্দু। CDFE- এর বৃহত্তম সম্ভাব্য ক্ষেত্রফল হবে-
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
The value of (PA)2−(PB)2+(PC)2−(PD)2 is equal to
View SolutionLet ABCD be a square with sides of unit lenght. Points E and F are taken on sides AB and AD, respectively,so that AE=AF. Let P be a point inside the squre ABCD.
Let a line passing through point A divides the sqaure ABD into two parts so that the area of one portion is double the other. then the length of the protion of line inside the square is
View Solution
