A rectangular billiard table has vertices at P(0,0),Q(0,7),R(10,7), and S(10,0). A small billiard ball starts at M(3,4) , moves in a straight line to the top of the table, bounces to the right side of the table, and then comes to rest at N(7,1) . The y− coordinate of the point where it hits the right side is 3.7 (b) 3.8 (c) 3.9 (d) 4Solution in Bengali

A

3.7

B

3.8

C

3.9

D

4

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

The correct Answer is:A

tanθ=a−13=7−a10−b
Also, tanθ=7−4b−3=3b−3
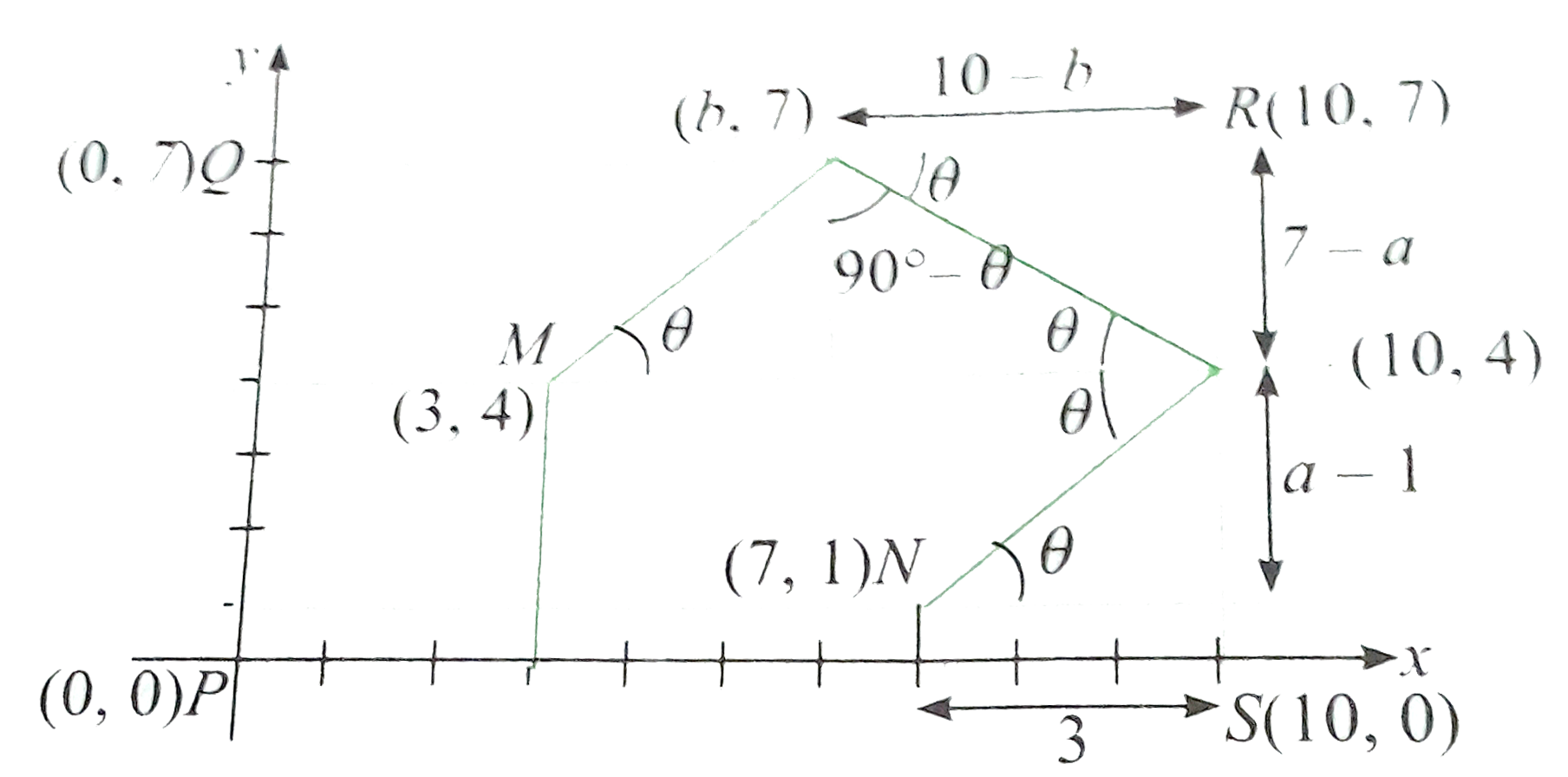
ocr_image
Hence, 3b−3=a−13=7−a10−b
From the first two relations, we have
9=ab−b−3a+3
or 3a+6=ab−b
From the last two relations, we have
10a−ab−10+b=21−3a
or 3a−ab+b=31
or ab−b=13a−31
Hence, from (1) and (2) ,
3a+6=13a−31
or 10a−37
or a=3.7

Updated on:21/07/2023
|
Class 12MATHSTHREE DIMENSIONAL GEOMETRY

Topper's Solved these Questions

Similar Questions