Point from. Solution in Bengali
A. parallelogram
B. rhombus
C. cyclic quadrilateral
D. none of these
The correct Answer is:C
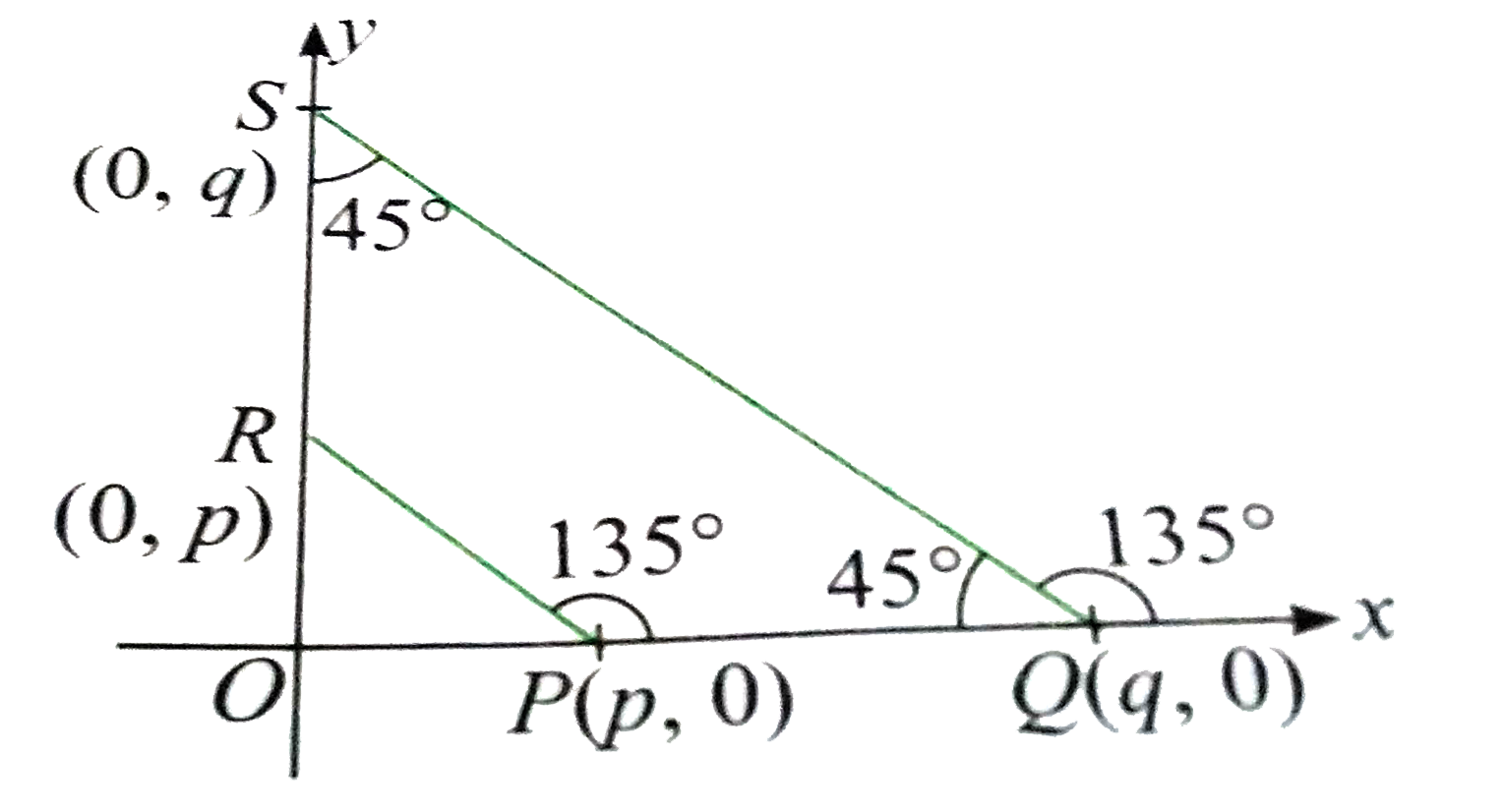
The diagram is self -explanatory. From the diagram, PQRS is a cyclic quadrilateral.
Topper's Solved these Questions
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Multiple correct
13 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Linked
10 Videos
- COORDINATE SYSYEM BOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSYEM EXERCISE - Concept applications 1.6
9 Videos
- COORDINATE SYSTEMBOOK - CENGAGE PUBLICATIONCHAPTER - COORDINATE SYSTEMEXERCISE - Multiple Correct Answers Type
2 Videos
- CROSS PRODUCTS BOOK - CENGAGE PUBLICATIONCHAPTER - CROSS PRODUCTS EXERCISE - DPP 2.2
13 Videos
Similar Questions
If (-6,-4), (3,5),(-2,1) are the vertices of a parallelogram, then remaining vertex cannot be
View SolutionFor points P=(x1,y1)and Q=(x2,y2) of the co-ordinate plane a new distance d(P,Q)=|x1−x2|+|y1−y2| is defined .Let O(0,0)and A(3,2). The set of points in first quadrant which are equidistant from O and A is
View SolutionFind the locus of a point whose distance from (a, 0) is equal to its distance from the y-axis.
View SolutionCoordinates of points on curve 5x2−6xy+5y2−4=0 which are nearest to origin are
View SolutionLet →a and →b be two vectors of equal magnitude 5 units. Let →p,→q be vectors such that →p=→a−→b and →q=→a+→b. If |→p×→q|=2{λ−(→a.→b)2}12, then value of λ is
View SolutionPoint P(p,0),Q(q,0),R(0,p),S(0,q) from parallelogram rhombus cyclic quadrilateral (d) none of these
View SolutionIf p, q, r are not in G.P. and ∣∣ ∣ ∣∣1qpα+qp1rpα+rqpα+qqα+r0∣∣ ∣ ∣∣=0 Show that pα2+2qα+r=0
View SolutionThe lines (p-q)x+(q-r)y+(r-p)=0(q-r)x+(r-p)y+(p-q)=0,(x-p)x+(p-q)y+(q-r)=
View Solutionसारणिक के प्रगुण का प्रयोग कर दिखाइए :
∣∣ ∣ ∣∣0p−qp−rq−p0q−rr−pr−q0∣∣ ∣ ∣∣=0
View Solution|(0,p-q,p-r),(q-p,0,q-r),(r-p,r-q,0)|=
View Solutionसारणिक ∣∣ ∣ ∣∣0p−qp−rq−p0q−rr−pr−q0∣∣ ∣ ∣∣ का मान ज्ञात कीजिए |
View SolutionIf p≠0,q≠0 and the roots of x2+px+q=0 are p and q, then (p, q) =
View SolutionPoint P(p,0),Q(q,0),R(0,p),S(0,q) from.
View Solutionरेखीय (p−q)x+(q−r)y+(r−p)=0
(q−r)x+(r−p)y+(p−q)=0
व (r−p)x+(p−q)y+(q−r)=0 है
View SolutionChoose the correct answer from the
bracket.The value of the determinant
∣∣ ∣ ∣∣0p−qp−rq−p0q−rr−pr−q0∣∣ ∣ ∣∣ is
View Solution
