Sketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥1 Solution in Tamil
(a) For x>2, first draw the lines x=2. All the points satisfying x>2 have abscissae greater than 2, i.e. all points lying to the right-hand side of x=2.
The region is as shown in the following figure.

(b) |y|≥1
So y≤−1ory≥1, i.e. all points have ordinate equal to ±1 or less than −1 or greater than 1. Hence all the points lying either on or below y=−1 or on or above y=1.
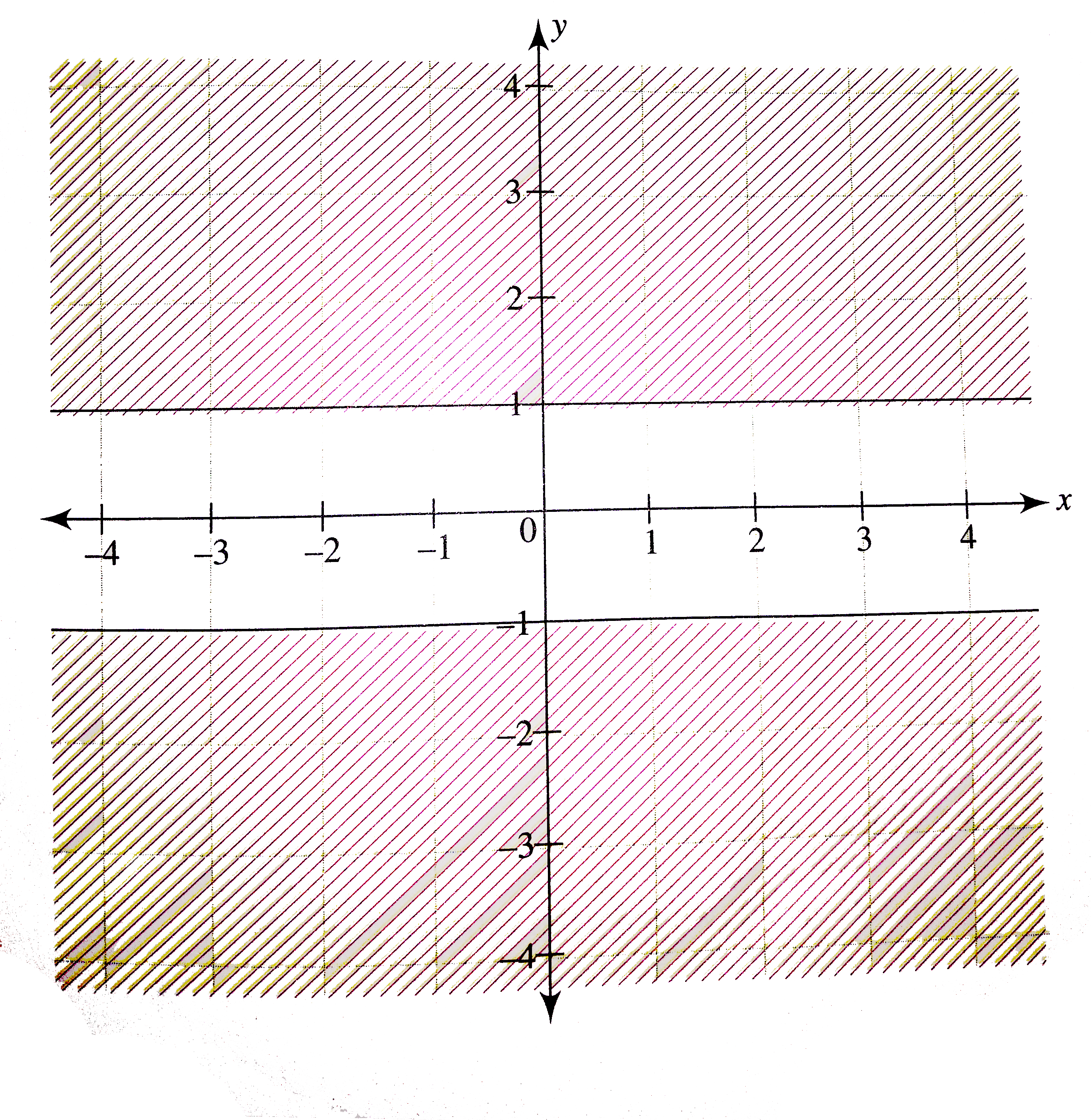
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises4videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y=1(1/x).
01:14View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=001:58View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
02:38View SolutionSketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥106:58View SolutionSketch the regions which points satisfy |x+y|≥2.
View SolutionSketch the region satisfying |x|<|y|.
02:29View SolutionSketch the origin in which the points satisfying the following inequality lie.
(i)2x−3y−5>0 (ii) −3x+4y+7>0
(iii)x>2 (iv) y>−3
03:34View SolutionSketch the origin in which the points satisfying the following inequalities lie.
(i)|x+y|<2 (ii) |2x−y|>3 (iii) |x|>|y|03:56View SolutionSketch the regions satisfying the following inequalities:
(a) x>2
(b) |y|≥105:11View SolutionSketch the regions which points satisfy |x+y|≥2.
09:09View SolutionSketch the region satisfying |x|<|y|.
03:38View SolutionSketch the origin in which the points satisfying the following inequality lie.
(i)2x−3y−5>0 (ii) −3x+4y+7>0
(iii)x>2 (iv) y>−3
04:15View SolutionSketch the origin in which the points satisfying the following inequalities lie.
(i)|x+y|<2 (ii) |2x−y|>3 (iii) |x|>|y|03:13View SolutionSketch the regions which points satisfy |x+y| ge 2 .
03:34View SolutionSketch the region satisfying |x| lt |y| .
03:23View Solution
