Let f:R→R:f(x)=(x+1) and g:R→R:g(x)=(x2−2). Write down the formulae for (gof). Solution in Tamil
For P(x,y), we have
2≤d1(P)+d2(P)≤4
⇒ 2≤|x−y|√2+|x+y|√2≤4 ltBrgt ⇒ 2√2≤|x−y|+|x+y|≤4√2
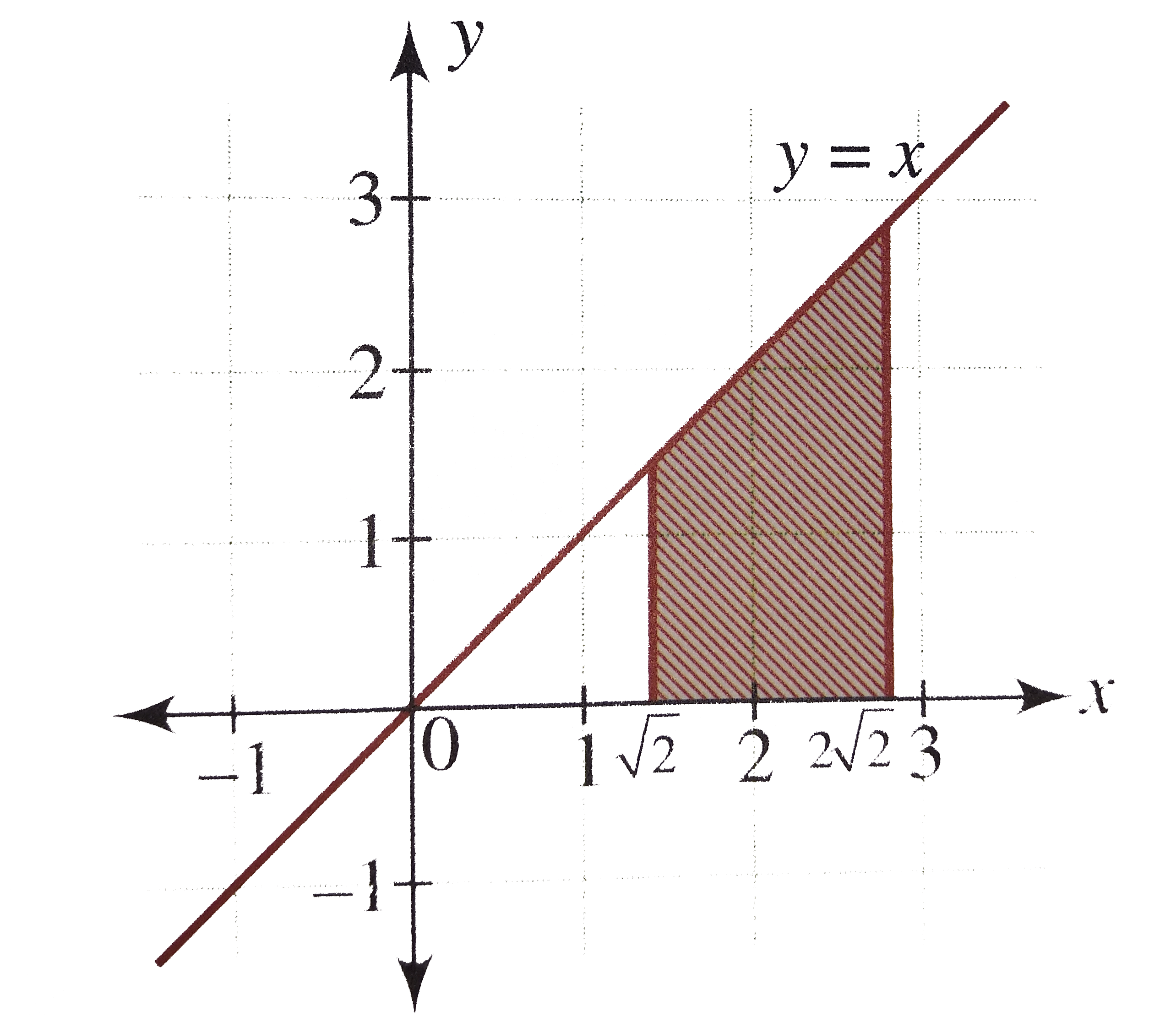
In the first quadrant if x>y, we have
2√2≤x−y+x+y≤4√2
or √2≤x≤2√2
The region of points satisfying these inequalities is as follows.
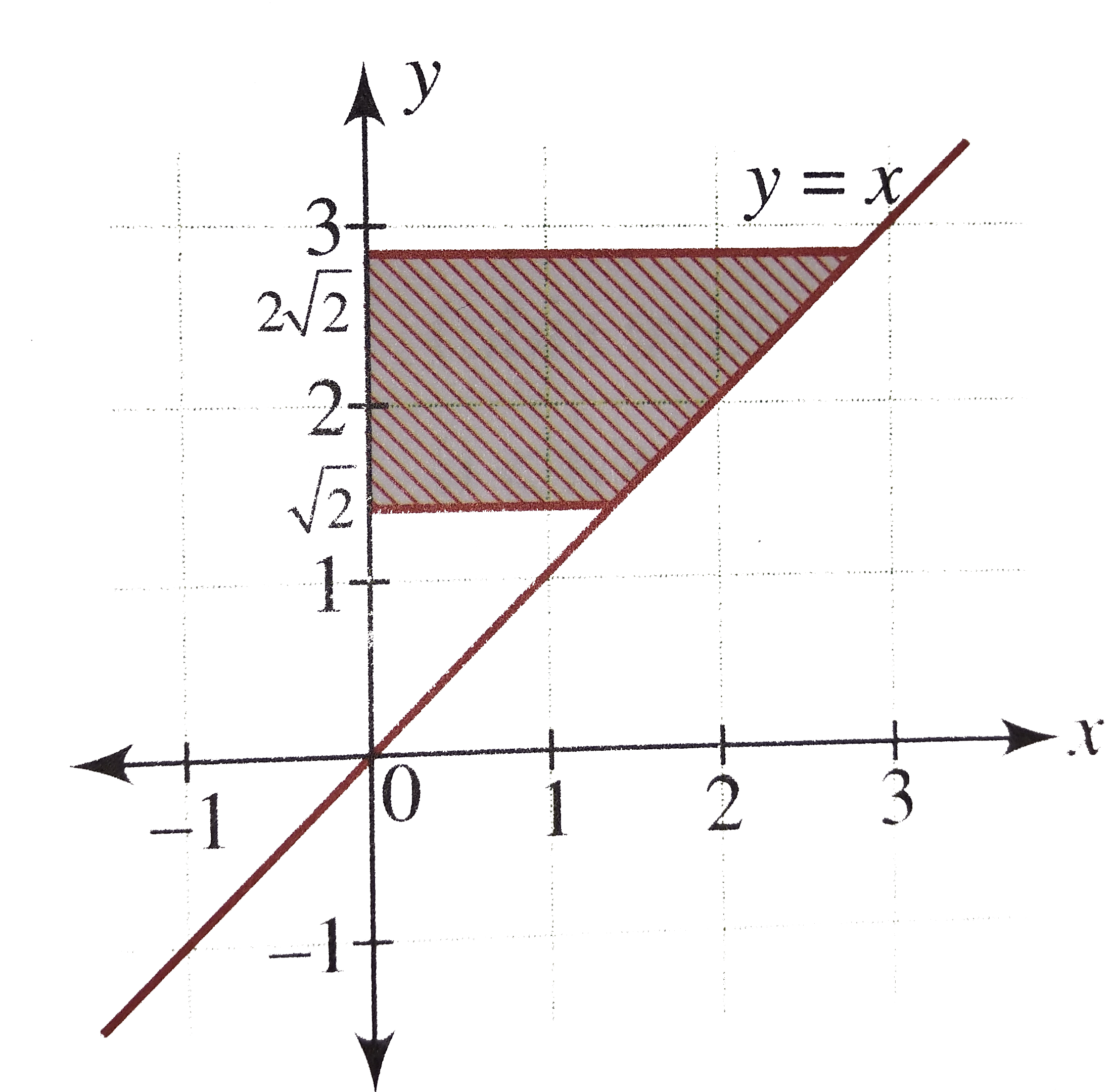
In the first quadrant if x<y, we have
2√2≤y−x+y≤4√2
or √2≤y≤2√2
The region of points satisfying these inequalities is as follows.
Combining the above two regions, we have the following.
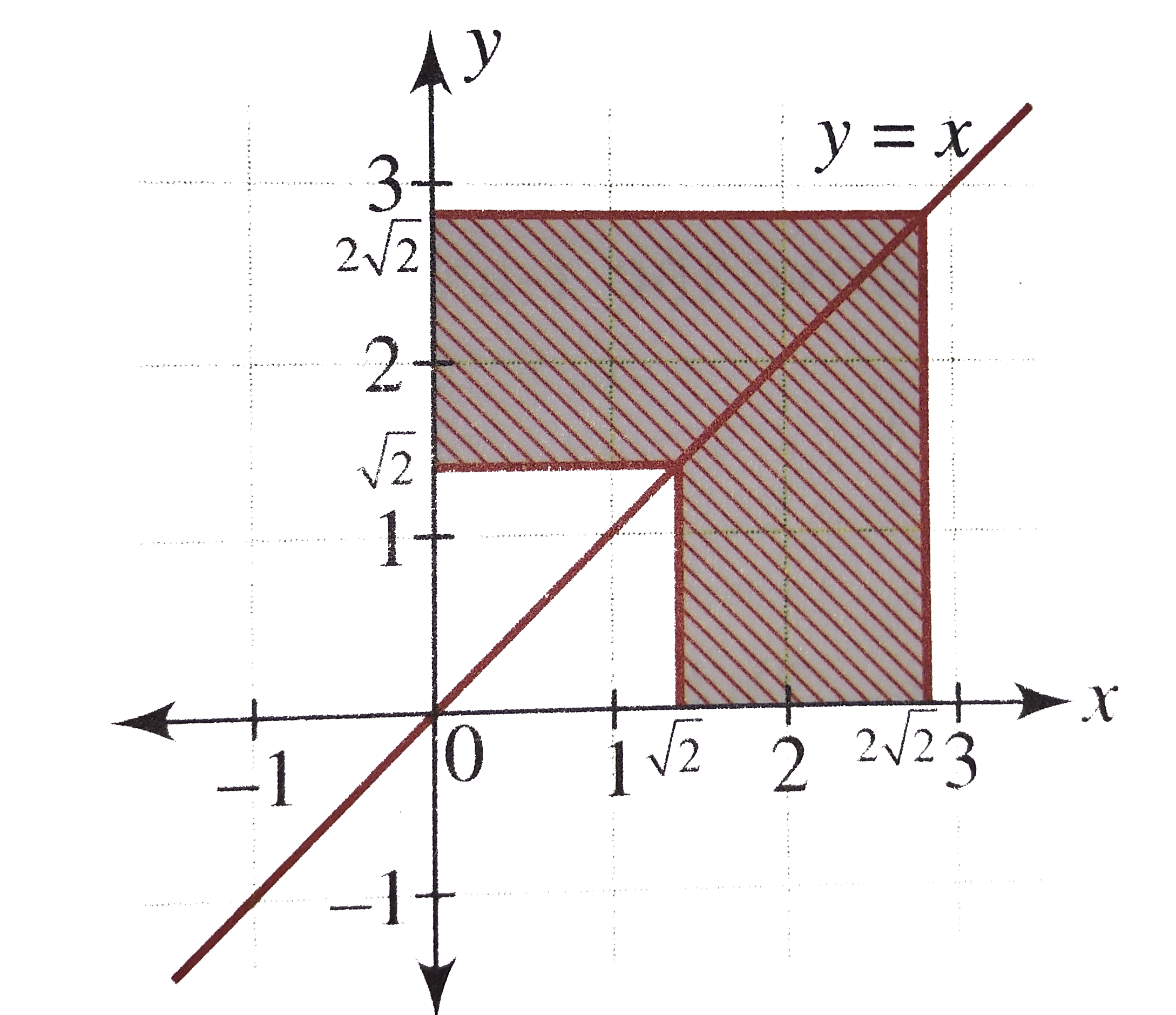
Area of the shaded region =((2√2)2−(√2)2)
=8−2=6 sq.units
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionLet f:R→R and g:R→R be defined by f(x)=x2 and g(x)=x+1. Show that fog≠gof.
View SolutionLet R be the set of real numbes. If f:R→R;f(x)=x2 and g:R→R;g(x)=2x+1 . Then, find fogandgof . Also, show that fog≠gof.
View SolutionLet f:R→ and g: RvecRbedef∈ed+1andg(x)=x−1. Show that fog=gof=IR.
View SolutionLet f:R rarr R and g:R rarr R be two functions such that (gof)(x)=sin^(2)x and (fog)(x)=sin(x^(2)) Find f(x) and g(x)
View SolutionLet f:R rarr R:f(x)=8x^(3) and g:R rarr R;g(x)=x^((1)/(3)). Find (gof) and (fog) and show,that gof!= fog.
View SolutionLet f:R rarr R:f(x)=x^(2),g:R rarr R:g(x)=tan x and h:R rarr R:h(x)=log x* Find a formula for ho(gof).Show that [ho(gof)]sqrt((pi)/(4))=0
View SolutionLet R be the set of real numbers. If f:R→R:f(x)=x2 and g:R→R;g(x)=2x+1. Then, find fog and gof . Also, show that fog≠gof.
View SolutionIf f:R rarr R,f(x)=2x-1 and g:R rarr R,g(x)=x^(2) then (gof)(x) equals
View Solutionयदि f:R→R तथा g:R→R फलन क्रमश: f(x)=cosx तथा g(x)=3x2 द्वारा परिभाषित है तो gof और fog ज्ञात कीजिएः gof≠fog.
View SolutionLet f:R→R be defined by f(x)=x2 and g:R→R be defined by g(x)=x+5. Then , (gof)(x) is equal to -
View SolutionIf f:R→R,g:R→R are defined by f(x)=3x−2,g(x)=x2+1, then find (i) (gof−1)(2)
View SolutionIf f:R→R,g:R→R are defined by f(x)=3x−2,g(x)=x2+1, then find (ii) (gof)(x−1)
View SolutionIf f:R→R,g:R→R are defined by f(x)=3x−1,g(x)=x2+1 then find
(ii) (gof)(x).
View Solution
