Question

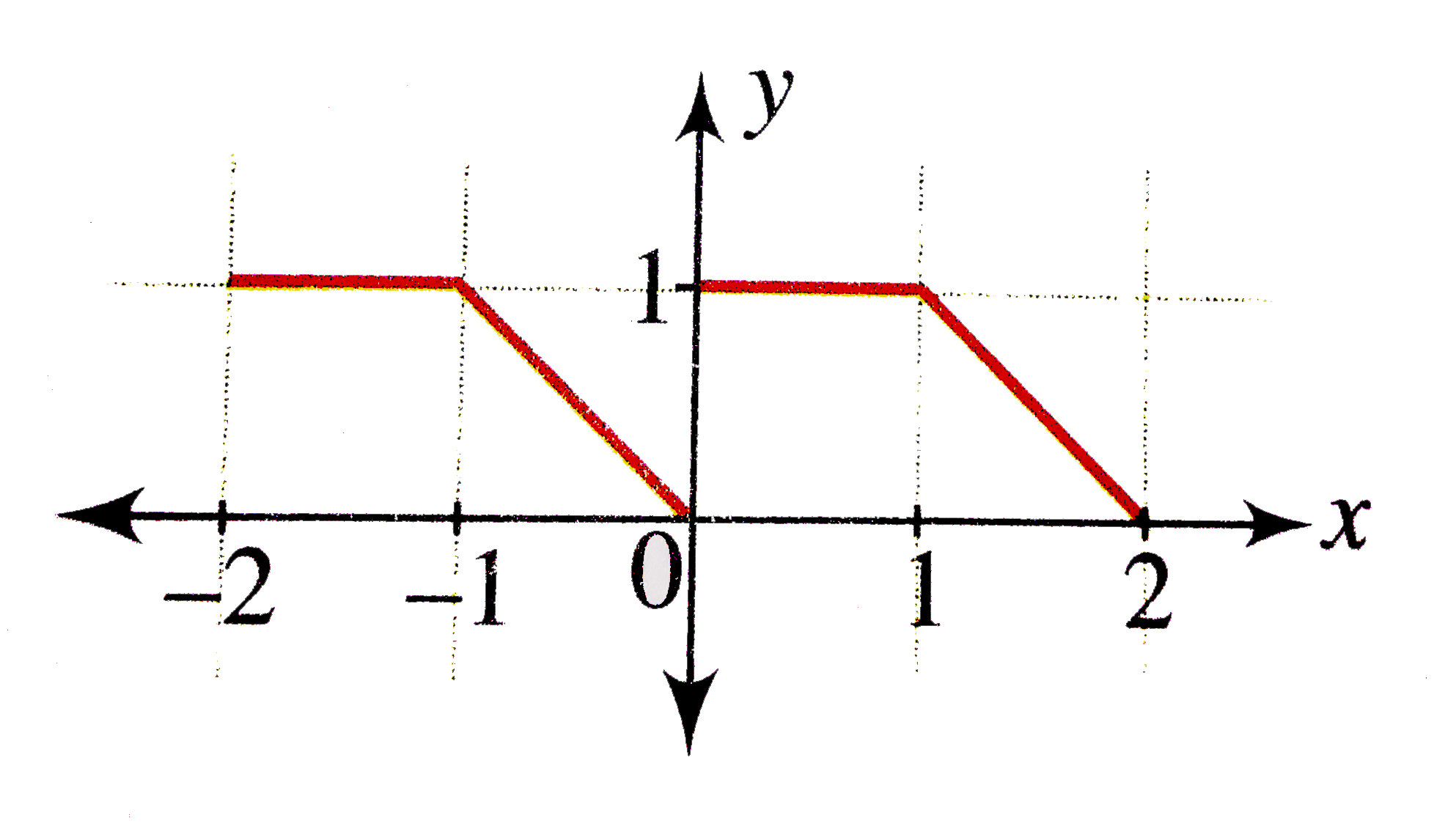
Given $f\left(x\right)$ is a periodic function with period 2 and it is defined as
$f\left(x\right)=\{\begin{array}{ccc}\left[\cos \frac{\pi x}{2}\right]+1\text{,}& & 0<x<1\\ 2-x\text{,}& & 1\le x<2\end{array}$
Here $[\cdot ]$ represents the greatest integer $\le x$. If $f\left(0\right)=1$, then draw the graph of the function for $x\in [-2,2]$.

Explanation

`f(x)= {{:([cos""(pix)/(2)]+1",",, 0 lt x lt 1), (2-x",",, 1 le x lt 2):}`
`" "= {{:(1",",, 0lt x lt 1), (2-x",",,1le x lt 2):}`

Since the function if periodic with period '2', the required graph for `x in [-2, 1]` is as follows.