Let f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function. Solution in Tamil
We have f(x)=[x]+1{x}+1
=⎧⎪
⎪
⎪
⎪⎨⎪
⎪
⎪
⎪⎩1x+1,0≤x<12x,1≤x<23x−1,2≤x<52
Each branch of the function is part of a rectangular hyperbola.
The graph of the function is as shown in the function is as shown in the following figure.
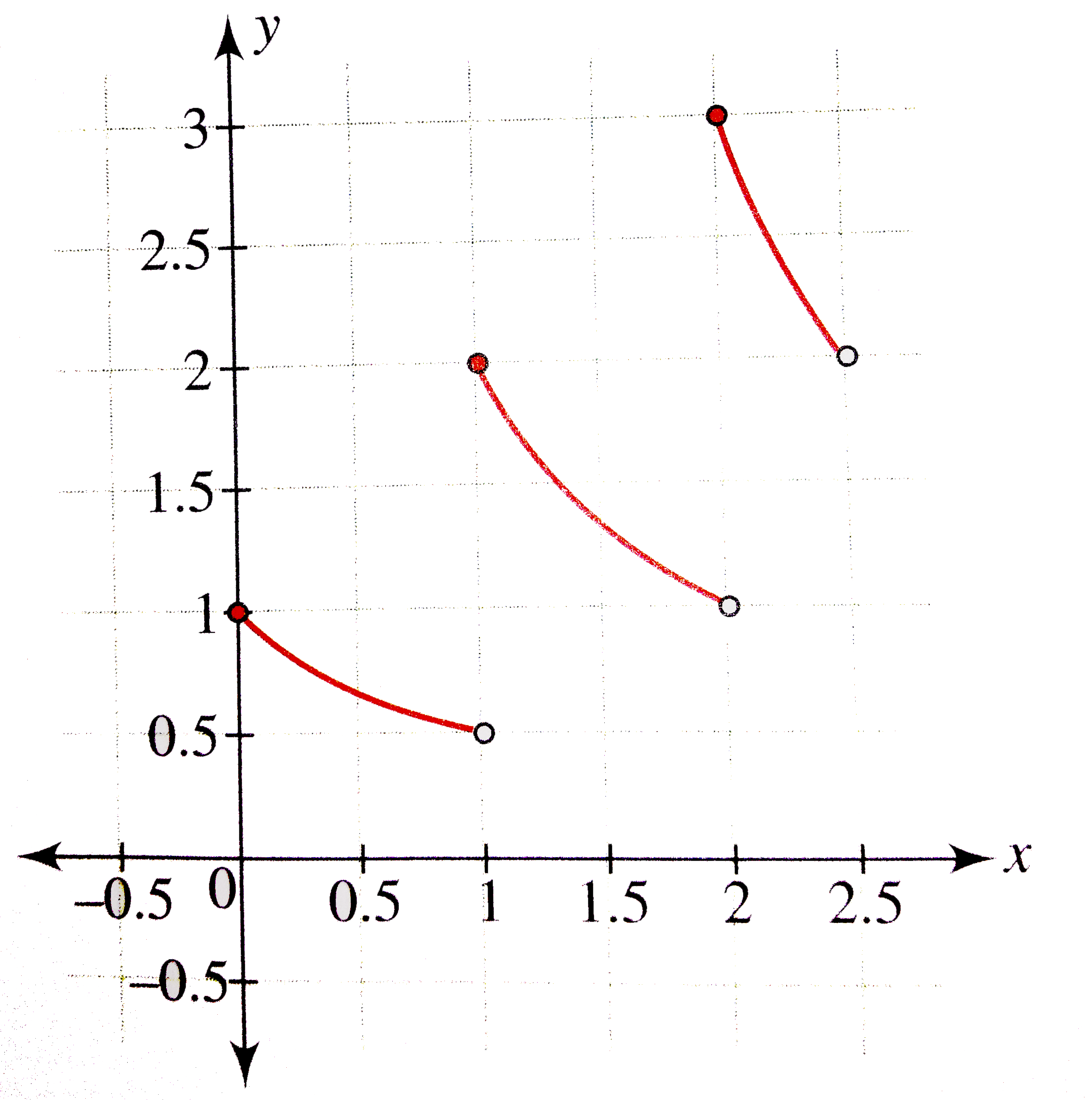
From the figure, the range of the function is [1/2,3].
Clearly, f(x) is a bijective function.
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercises
4 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of y=1(1/x).
View SolutionSketch the graph of an example of a rational function f that satisfies all the given conditions.
(i) f(0)=0,f(1),limx→∞f(x)=0,f is odd
(ii) limx→0+f(x)=∞,limx→0−f(x)=−∞,limx→∞f(x)=1,limx→−∞f(x)=1
(iii) limx→−2f(x)=∞,limx→−∞f(x)=3,limx→∞f(x)=3,f(0)=0
View SolutionDraw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionIf (x)=[x],0<={x}<0.5 and f(x)=[x]+1,0.5<{x}<1 then prove that f(x)=-f(-x) (wherel.] and {.} represent the greatest integer function and the fractional part function, respectively).
View SolutionIf f(x)=[2x+1]+[2-2x]+{x}+{-x} where [.] represents greatest integer function and {.} represents fractional function then (1) f(x) is a periodic functional with fundamental period =1 (2) f(x) has no fundamental period (3) Range of f(x) is {3,4} (4) Range of f(x) is {3}
View SolutionFind the range of each of the following functions: (where {.} and [.] represents fractional part and greatest integer part functions respectively)
f(x)=11+√x
View SolutionFind the range of the following functions: (where {.} and [.] represent fractional part and greatest integer part functions respectively)
f(x)=1−|x−2|
View SolutionFind the range of the following functions: (where {.} and [.] represent fractional part and greatest integer part functions respectively)
f(x)=x4−2x2+5
View SolutionLet f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function.
View Solutionf(x)=[x]+1{x}+1forf:[0,52)→(12,3], where [.] repesents the greatest integer function and {.} represents the fractional part of x then which of the following is true ?
View SolutionDraw the graph of f(x)=(2^(x))/(2^([x])) where [.] represents greatest integer function and find the domain and range.
View SolutionIf f(x)=[x],0≤{x}<0.5andf(x)=[x]+1,0.5<{x}<1 then prove that f (x) = -f(-x) (where[.] and{.} represent the greatest integer function and the fractional part function, respectively).
View SolutionLet f(x)=[x]+1{x}+1 for f:[0,52)→(12,3], where [⋅] represents the greatest integer function and {⋅} represents the fractional part of x.
Draw the graph of y=f(x). Prove that y=f(x) is bijective. Also find the range of the function.
View SolutionIf f(x)=[x],0≤{x}<0.5andf(x)=[x]+1,0.5<{x}<1 then prove that f (x) = -f(-x) (where[.] and{.} represent the greatest integer function and the fractional part function, respectively).
View SolutionFind the range of each of the following functions: (where {.} and [.] represents fractional part and greatest integer part functions respectively)
f(x)=11+√x
View SolutionFind the range of the following functions: (where {.} and [.] represent fractional part and greatest integer part functions respectively)
f(x)=1−|x−2|
View Solution
