Question

Sketch the regions satisfying the following inequalities:
(a) $x>2$
(b) $\left|y\right|\ge 1$

Explanation

(a) For `x gt 2`, first draw the lines `x=2`. All the points satisfying `x gt 2` have abscissae greater than 2, i.e. all points lying to the right-hand side of `x=2`.
The region is as shown in the following figure.

(b) `|y| ge 1`
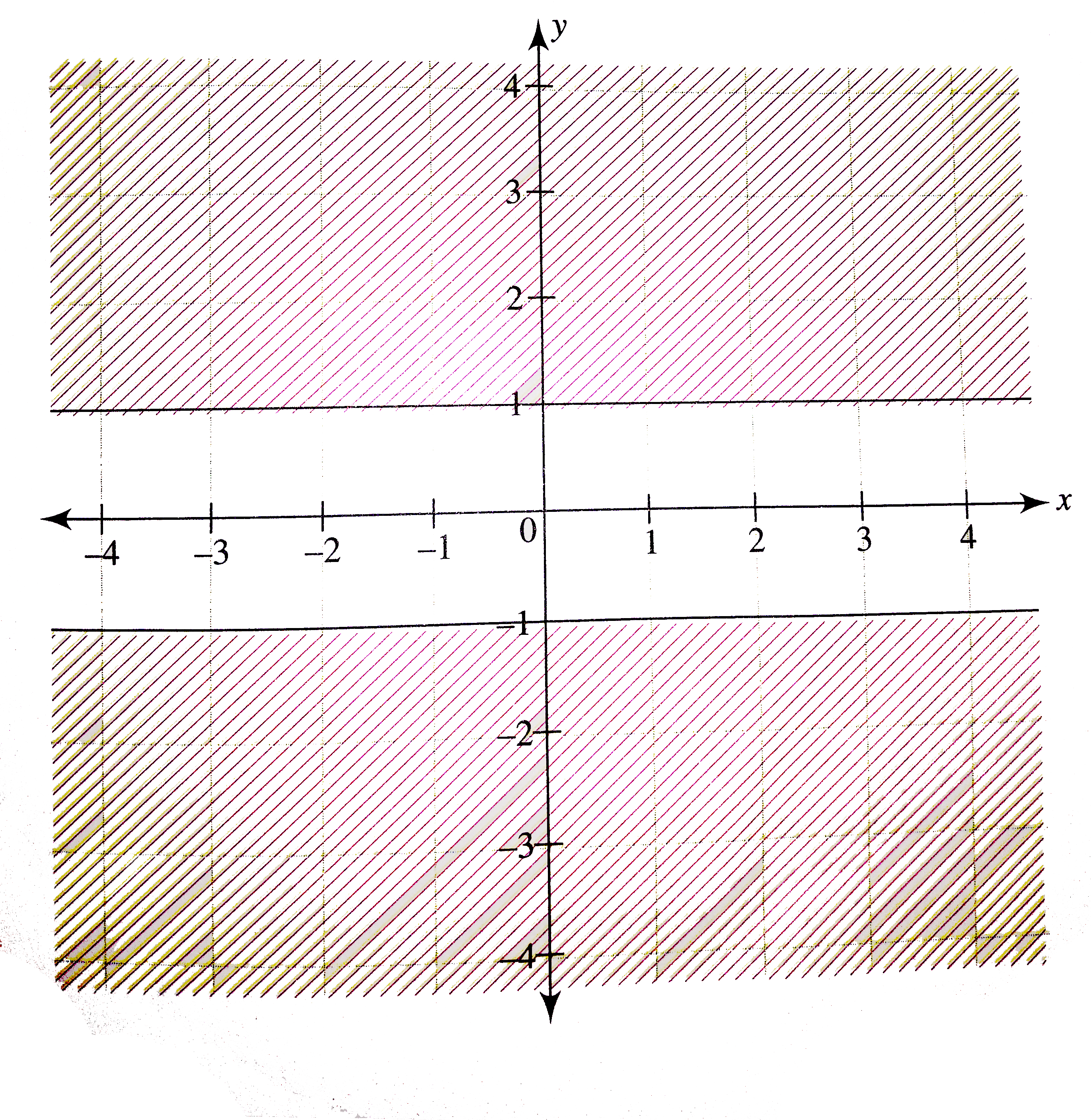
So `y le -1 or y ge 1`, i.e. all points have ordinate equal to `pm 1` or less than `-1` or greater than 1. Hence all the points lying either on or below `y=-1` or on or above `y=1`.