Question

${\displaystyle x-y\le 2}$

Answer

N/a

Explanation

Given inequation : `x - y le 2`
Corresponding equation : `x - y = 2`
This line cuts the X-axis at point A (2, 0) and Y-axis at point B (0, 2).
Draw a line joining points A and B.
At point (0, 0), from the inequation , `0le 2` (True)

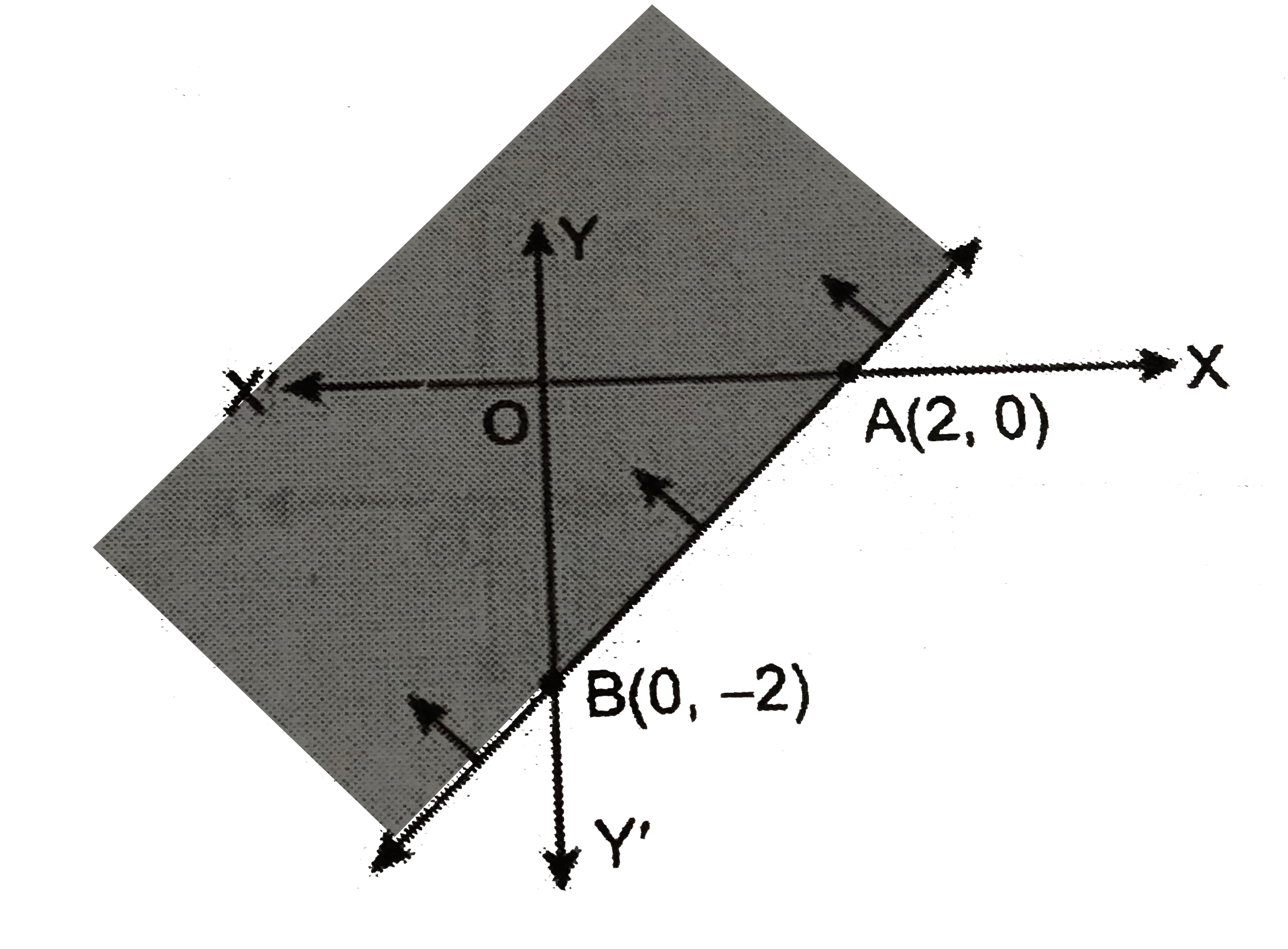
Now, shade that region of XY-plane divided by line AB in which (0, 0) lies.