x−2y≤4
The correct Answer is:N/a
To solve the inequality x−2y≤4 graphically, we will follow these steps:
Step 1: Convert the inequality to an equation
We start by converting the inequality into an equation to find the boundary line:
x−2y=4
Step 2: Find the intercepts
To graph the line, we need to find the x-intercept and y-intercept.
Finding the x-intercept:
Set y=0:
x−2(0)=4⟹x=4
So, the x-intercept is (4,0).
Finding the y-intercept:
Set x=0:
0−2y=4⟹−2y=4⟹y=−2
So, the y-intercept is (0,−2).
Step 3: Plot the points
Now we plot the points (4,0) and (0,−2) on the Cartesian plane.
Step 4: Draw the boundary line
Draw a straight line through the points (4,0) and (0,−2). Since the inequality is less than or equal to (≤), we will use a solid line to indicate that points on the line are included in the solution.
Step 5: Determine the shading region
To determine which side of the line to shade, we can test a point that is not on the line. A common choice is the origin (0,0).
Substituting (0,0) into the inequality:
0−2(0)≤4⟹0≤4
This is true, so we shade the region that includes the origin.
Step 6: Final representation
The shaded region represents all the solutions to the inequality x−2y≤4. Any point in this region satisfies the inequality.
Summary
The solution to the inequality x−2y≤4 is represented graphically by the shaded region below and including the line x−2y=4.
---
We start by converting the inequality into an equation to find the boundary line:
x−2y=4
To graph the line, we need to find the x-intercept and y-intercept.
Set y=0:
x−2(0)=4⟹x=4
So, the x-intercept is (4,0).
Set x=0:
0−2y=4⟹−2y=4⟹y=−2
So, the y-intercept is (0,−2).
Now we plot the points (4,0) and (0,−2) on the Cartesian plane.
Draw a straight line through the points (4,0) and (0,−2). Since the inequality is less than or equal to (≤), we will use a solid line to indicate that points on the line are included in the solution.
To determine which side of the line to shade, we can test a point that is not on the line. A common choice is the origin (0,0).
0−2(0)≤4⟹0≤4
This is true, so we shade the region that includes the origin.
The shaded region represents all the solutions to the inequality x−2y≤4. Any point in this region satisfies the inequality.
The solution to the inequality x−2y≤4 is represented graphically by the shaded region below and including the line x−2y=4.
Topper's Solved these Questions
- LINEAR INEQUALITIESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR INEQUALITIESExercise:NCERT QUESTION
Explore 51 Videos
- LINEAR INEQUALITIESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR INEQUALITIESExercise:MISCELLANEOUS EXERCISE
Explore 14 Videos
- LINEAR INEQUALITIESBook:NAGEEN PRAKASHAN ENGLISHChapter:LINEAR INEQUALITIESExercise:MISCELLANEOUS EXERCISE
Explore 14 Videos
- LIMITS AND DERIVATIVESBook:NAGEEN PRAKASHAN ENGLISHChapter:LIMITS AND DERIVATIVESExercise:Miscellaneous Exercise
Explore 30 Videos
- MATHEMATICAL REASONING Book:NAGEEN PRAKASHAN ENGLISHChapter:MATHEMATICAL REASONING Exercise:Misellaneous exercise
Explore 7 Videos
Similar Questions
Knowledge Check
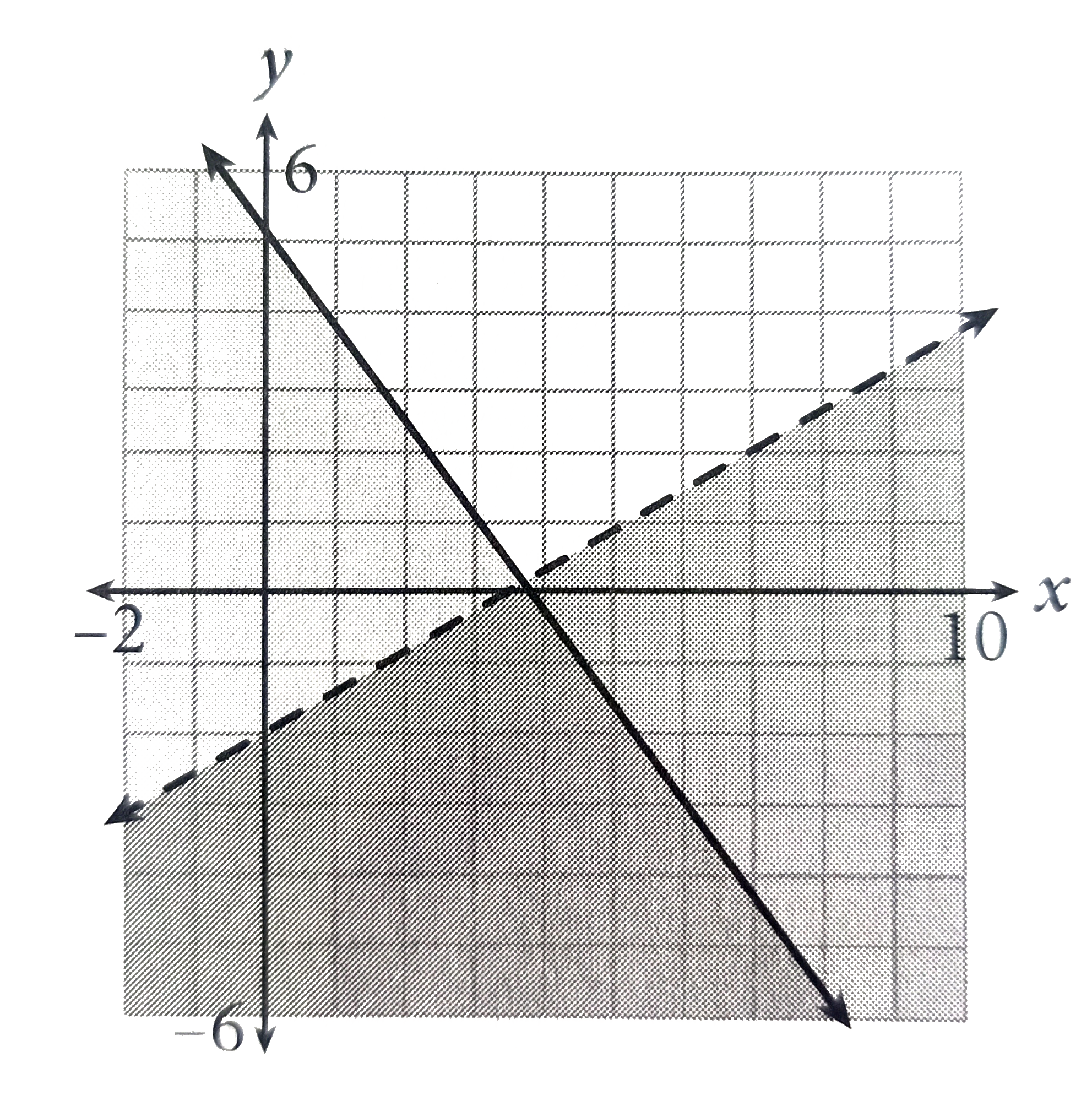
The figure above shows the solution set for this system of inequalities:
⎧⎨⎩x<35x−2y≤−43x+5
Which of the following is NOT is solution to this system ?A(−1,−4)B(1,−1)C(4,−1)D(6,−3)
The area defined by 2≤|x+y|+|x−y|≤4 is
View Solutionx−y≤2,x+y≤4,x≥0,y≥0
View SolutionShow the common solution of given inequalities and shade the region bounded by them .
3x+2y≤150,x+4y≤80,x≤15,y≥0,x≥0
View SolutionSolve the linear inequalities.
2x+y≥4,x+y≤3,2x−3y≤6
View Solution2x+y≤6,x+2y≤8,x≥0,y≥0
View Solutionx+y≤10,4x+3y≤24,x≥0,y≥0
View Solutionx+2y≤10,x+y≥1,x−y≤0,x≥0,y≥0
View Solution

