Question

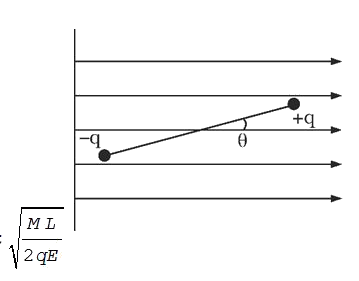
A point particle of mass M is attached to one end of a massless rigid non-conducting rod of length L. Another point particle of the same mass is attached to the other end of the rod. The two particles carry charges $+q$ and $-q$ respectively. This arrangement is held in a region of a uniform electric field E such that the rod makes a small angle $\theta$ (say of about 5 degree) with the field direction, fig. Find an expression for the minimum time needed for the rod to become parrallel to the field after it is set free.

Answer

`(pi)/(2) ((ML)/( 2qE))^(1//2)`

Explanation

`((pi)/(2) ((ML)/( 2q E))^(1//2))`
The rod will act as a dipole moment,
P = `q xx L`
placed in an electric field of strength B, it will be acted upon by a couple of strength.
`C = - PE sin theta = - q LE sin theta`
As `theta` is small `sin theta ~~ theta`
`C = - qL E theta `
This couple will set rod into simple harmonic motion with time period.
`T = (2 pi )/( sqrt(u)) ` where ` mu = (qL E)/(l)`
` I = M ((L)/(2))^(2) + ((L)/(2))^(2) = (ML^(2))/( 2) and T = (2)/(sqrt(( 2 qE)/(ML)) = 2pi sqrt((ML)/(2 qE)`
Therefore, expected time of motion ` = (T)/(4) = (2pi)/(4) sqrt((ML)/(qE)) = (pi)/(2) ((ML)/( 2 q E))^(1//2)`