A particle of mass 10−3 kg and charge 1.0 c is initially at rest At time t=0 the paritcle comes under the influence of an electric field ˆE(t)=E0sinωtˆi where E0=1.0NC−1 and ω=103rads−1 consider the effect of only the electrical force on the particle .Then the maximum speed in m s−1 attained by the paritcle at subsequent times is ______________
The correct Answer is:2
To solve the problem step by step, we will follow the reasoning presented in the video transcript.
Step 1: Identify the given parameters
- Mass of the particle, m=10−3kg
- Charge of the particle, q=1.0C
- Electric field, ^E(t)=E0sin(ωt)^i where E0=1.0N/C and ω=103rad/s
Step 2: Calculate the force on the particle
The force F acting on the particle due to the electric field is given by:
F=q^E(t)=qE0sin(ωt)^i
Substituting the values:
F=1.0⋅1.0sin(103t)^i=sin(103t)^iN
Step 3: Relate force to acceleration
According to Newton's second law, F=ma, where a is the acceleration. Therefore, we can write:
ma=sin(103t)
Thus, the acceleration a is given by:
a=Fm=sin(103t)10−3=103sin(103t)m/s2
Step 4: Relate acceleration to velocity
Acceleration is the rate of change of velocity:
a=dvdt
So, we can express this as:
dvdt=103sin(103t)
Step 5: Integrate to find velocity
To find the velocity v, we integrate the acceleration:
dv=103sin(103t)dt
Integrating both sides:
v=∫103sin(103t)dt
The integral of sin(kt) is −1kcos(kt)+C, where k=103:
v=−103103cos(103t)+C=−cos(103t)+C
Since the particle is initially at rest (v=0 at t=0):
0=−cos(0)+C⟹C=1
Thus, the velocity becomes:
v(t)=1−cos(103t)
Step 6: Find the maximum velocity
The maximum value of v(t) occurs when cos(103t) is at its minimum value, which is -1:
vmax=1−(−1)=2m/s
Conclusion
The maximum speed attained by the particle is:
2m/s
- Mass of the particle, m=10−3kg
- Charge of the particle, q=1.0C
- Electric field, ^E(t)=E0sin(ωt)^i where E0=1.0N/C and ω=103rad/s
The force F acting on the particle due to the electric field is given by:
F=q^E(t)=qE0sin(ωt)^i
Substituting the values:
F=1.0⋅1.0sin(103t)^i=sin(103t)^iN
According to Newton's second law, F=ma, where a is the acceleration. Therefore, we can write:
ma=sin(103t)
Thus, the acceleration a is given by:
a=Fm=sin(103t)10−3=103sin(103t)m/s2
Acceleration is the rate of change of velocity:
a=dvdt
So, we can express this as:
dvdt=103sin(103t)
To find the velocity v, we integrate the acceleration:
dv=103sin(103t)dt
Integrating both sides:
v=∫103sin(103t)dt
The integral of sin(kt) is −1kcos(kt)+C, where k=103:
v=−103103cos(103t)+C=−cos(103t)+C
Since the particle is initially at rest (v=0 at t=0):
0=−cos(0)+C⟹C=1
Thus, the velocity becomes:
v(t)=1−cos(103t)
The maximum value of v(t) occurs when cos(103t) is at its minimum value, which is -1:
vmax=1−(−1)=2m/s
The maximum speed attained by the particle is:
2m/s
Topper's Solved these Questions
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN
65 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE
52 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
1 Videos
Similar Questions
Two particles of masses 1kg and 2kg respectively are initially 10m aprt. At time t=0, they start moving towards each other with uniform speeds 2m/s and 1m/s respectively. Find the displacement of their centre of mass at t=1s.
View SolutionA particle of charge q and mass m starts moving from the origin under the action of an electric field →E=E0ˆiand→B=B0ˆi with a velocity →v=v0ˆj. The speed of the particle will become 2v0 after a time.
View Solution
Knowledge Check
A particle of mass m and charge Q is placed in an electric filed W which varies with time t as E = E0sinωt. It will undergo simple harmonic motion of amplitude.
AQE20mω2BQE0mω2C√QE0mω2DQE0mωA particle of mass m and charge q has and initial velocity →v=υ0ˆj. If an electric field →E=→–––(0)ˆi and magnetic field →B=B0ˆi act on the particle, its speed will double after a time :
At=2mv0qE0Bt=2B0qmv0Ct=√3B0qmv0Dt=√3mv0qE0
A particle of mass m and charge q has and initial velocity →v=υ0ˆj. If an electric field →E=→–––(0)ˆi and magnetic field →B=B0ˆi act on the particle, its speed will double after a time :
View SolutionA particle of charge q and mass m is subjected to an electric field E=E0(1−ax2) in the x - direction, where a and E0 are constants. Initially the particle was at rest at x = 0. Other than the initial position the kinetic energy of the particle becomes zero when the distance of the particle from the origin is :
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?
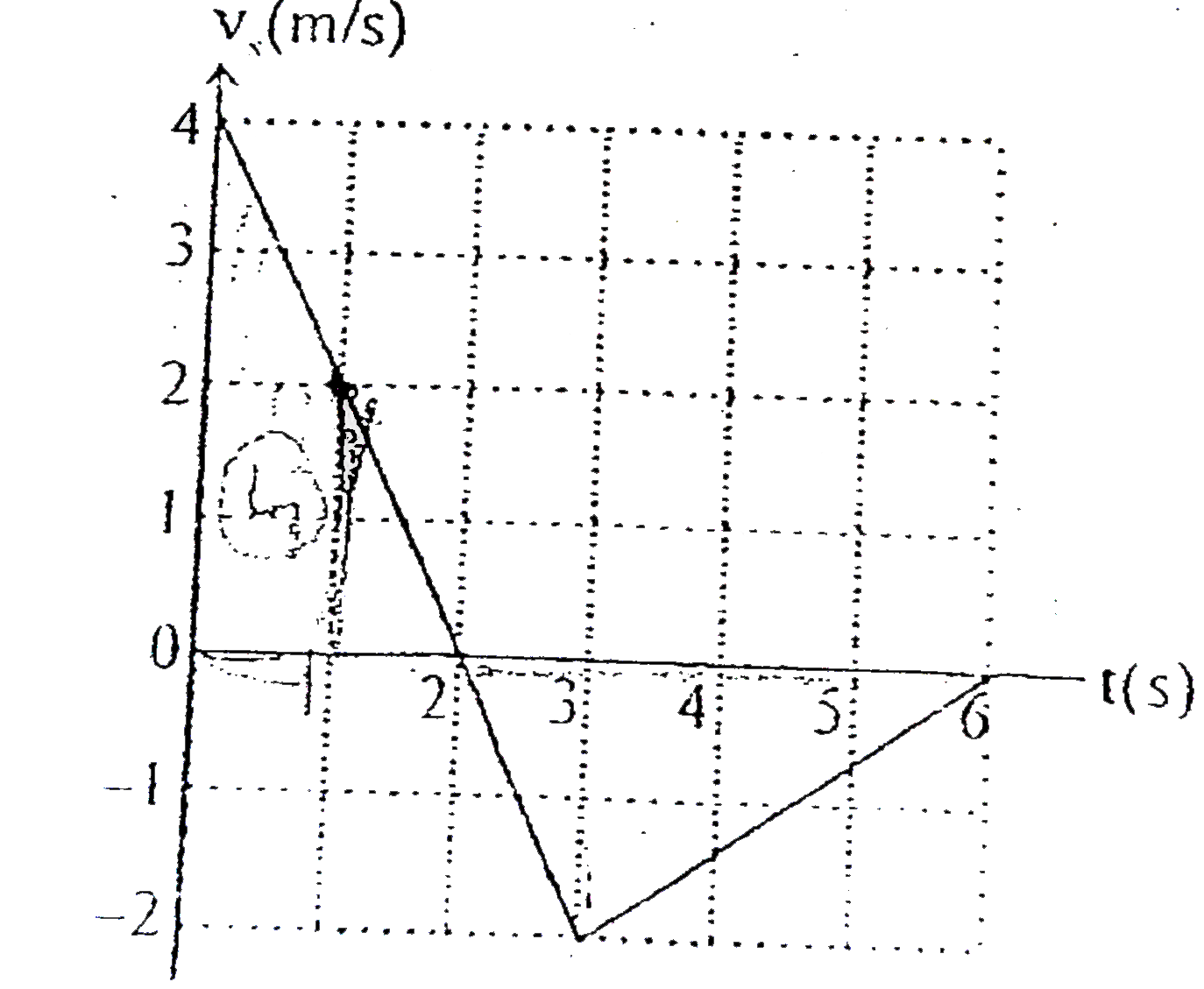
View SolutionThe emf and current in a circuit are such that E=E0sinωt and I=I0sin(ωt−θ). This AC circuit contains
View Solutionthe angular velocity omega of a particle varies with time t as ω=5t2+25rads. the angular acceleration of the particle att=1s is
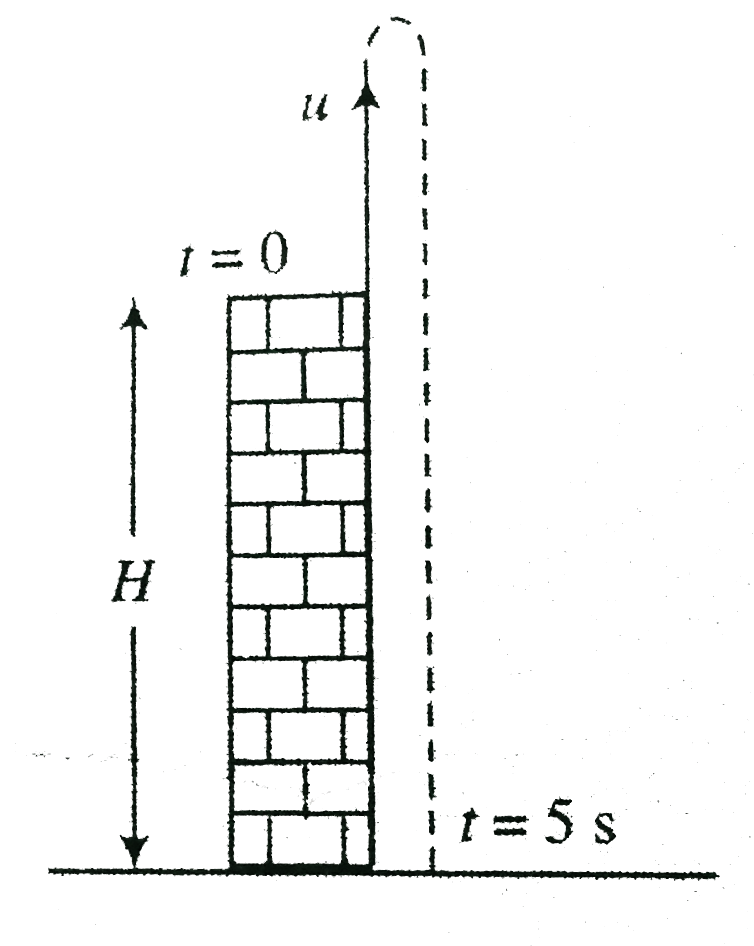
View SolutionA particle is projected up with initial speed u=10ms−1 from the top of a bitlding at time t=0. At time t=5s the particle strikes the fround. Find the height of the building.
 .
.
View Solution
