Four point charges, each of +q, are rigidly fixed at the four corners of a square planar soap film of side 'a'. The surface tension of the soap film is γ. The system of charges and planar film are in equilibrium, and a=k[q2γ]1/N, where 'K' is a constant. Then N is
The correct Answer is:3
To solve the problem, we need to analyze the forces acting on the charges and the effect of surface tension on the soap film. Here's a step-by-step breakdown of the solution:
Step 1: Understanding the Setup
We have four point charges, each of charge +q, fixed at the corners of a square soap film of side length a. The surface tension of the soap film is denoted by γ.
Step 2: Calculate the Force Due to Surface Tension
The surface tension force acts along the edges of the soap film. Since there are two surfaces (top and bottom) and each side has a length a, the total force due to surface tension is:
Ftension=2γa
Step 3: Calculate the Electrostatic Forces
Each charge experiences forces due to the other three charges. The force F between two charges q separated by a distance r is given by Coulomb's law:
F=kq2r2
where k is Coulomb's constant.
For a charge at a corner of the square, the distances to the adjacent charges are a and to the diagonal charge is √2a.
Step 4: Calculate the Net Electrostatic Force on One Charge
The force due to the two adjacent charges (each at distance a) is:
Fadj=2(kq2a2)
The force due to the diagonal charge (at distance √2a) is:
Fdiag=kq2(√2a)2=kq22a2
Step 5: Resolve Forces
The forces from the two adjacent charges act at 90∘ to each other. The resultant force from these two can be calculated using the Pythagorean theorem:
Fresultant, adj=√(Fadj)2+(Fadj)2=√2(kq2a2)2=kq2a2√2
The total force acting on the charge is then:
Ftotal=Fresultant, adj+Fdiag=kq2a2√2+kq22a2
Step 6: Equilibrium Condition
For the system to be in equilibrium, the total electrostatic force must balance the surface tension force:
Ftotal=Ftension
Substituting the expressions we derived:
kq2a2√2+kq22a2=2γa
Step 7: Rearranging for a
We can factor out kq2a2:
kq2a2(√2+12)=2γa
Step 8: Solve for a
Rearranging gives:
a3=kq2γ(√2+12)
This implies:
a=k(q2γ)1/3
Step 9: Identify N
From the given equation a=k(q2γ)1/N, we see that N=3.
Final Answer
Thus, the value of N is:
3
We have four point charges, each of charge +q, fixed at the corners of a square soap film of side length a. The surface tension of the soap film is denoted by γ.
The surface tension force acts along the edges of the soap film. Since there are two surfaces (top and bottom) and each side has a length a, the total force due to surface tension is:
Ftension=2γa
Each charge experiences forces due to the other three charges. The force F between two charges q separated by a distance r is given by Coulomb's law:
F=kq2r2
where k is Coulomb's constant.
The force due to the two adjacent charges (each at distance a) is:
Fadj=2(kq2a2)
The force due to the diagonal charge (at distance √2a) is:
Fdiag=kq2(√2a)2=kq22a2
The forces from the two adjacent charges act at 90∘ to each other. The resultant force from these two can be calculated using the Pythagorean theorem:
Fresultant, adj=√(Fadj)2+(Fadj)2=√2(kq2a2)2=kq2a2√2
Ftotal=Fresultant, adj+Fdiag=kq2a2√2+kq22a2
For the system to be in equilibrium, the total electrostatic force must balance the surface tension force:
Ftotal=Ftension
Substituting the expressions we derived:
kq2a2√2+kq22a2=2γa
We can factor out kq2a2:
kq2a2(√2+12)=2γa
Rearranging gives:
a3=kq2γ(√2+12)
This implies:
a=k(q2γ)1/3
From the given equation a=k(q2γ)1/N, we see that N=3.
Thus, the value of N is:
3
Topper's Solved these Questions
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE MAIN
Explore 65 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Book:VMC MODULES ENGLISHChapter:ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT Exercise:IMPECCABLE
Explore 52 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE
Explore 1 Video
Similar Questions
Four identical charges each .q. are placed at four corners of a square of side .a.. Find the charge to be placed at the centre of the square so that the system of charges is in equilibrium
View SolutionFour charges equal to −Q are placed at the four corners of a square and a charge q is at its centre. If the system is in equilibrium the value of q is
View Solution
Knowledge Check
Four equal charges Q are placed at the four corners of a square of each side is 'a'. Work done in removing a charge −Q from its centre to infinity is
AzeroB√2q2πε0aC√2qπε0aDq2πε0a
Four small point charges (each of equal magnitude q) are placed at four corners of a regular tetrahedron of side a. find out potential energy of charge system
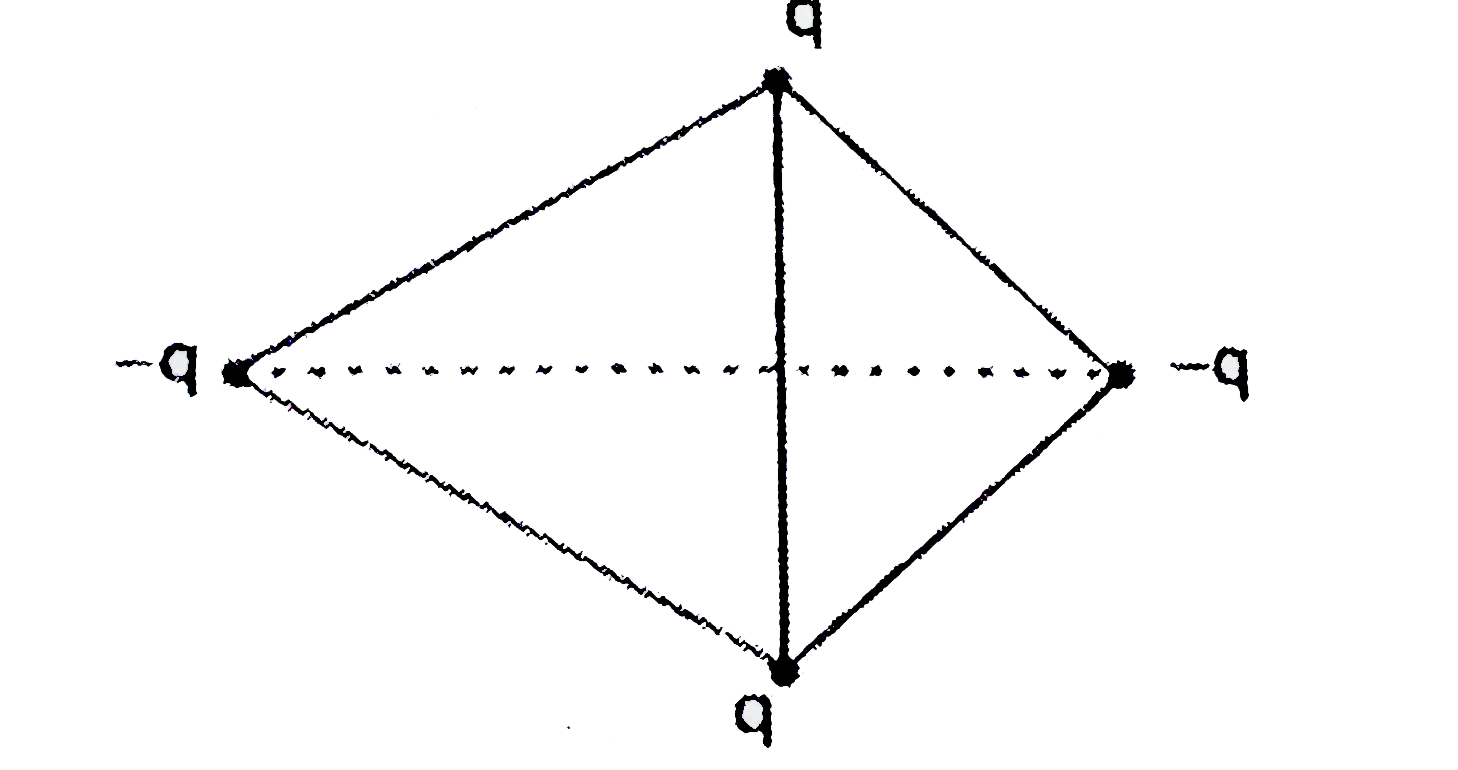
View SolutionFour identical point charges q are placed at four corners of a square of side a. Find the potential energy of the charge system.
 .
.
View SolutionFour identical charges Q are fixed at the four corners of a square of side a. The electric field at a point P located symmetrically at a distance a/√2 from the center of the square is
View SolutionFour positive charges (2√2−1)Q are arranged at the four corners of a square. Another charge q is placed at the centre of the square. Resulting force acting on each corner charge is zero if q is
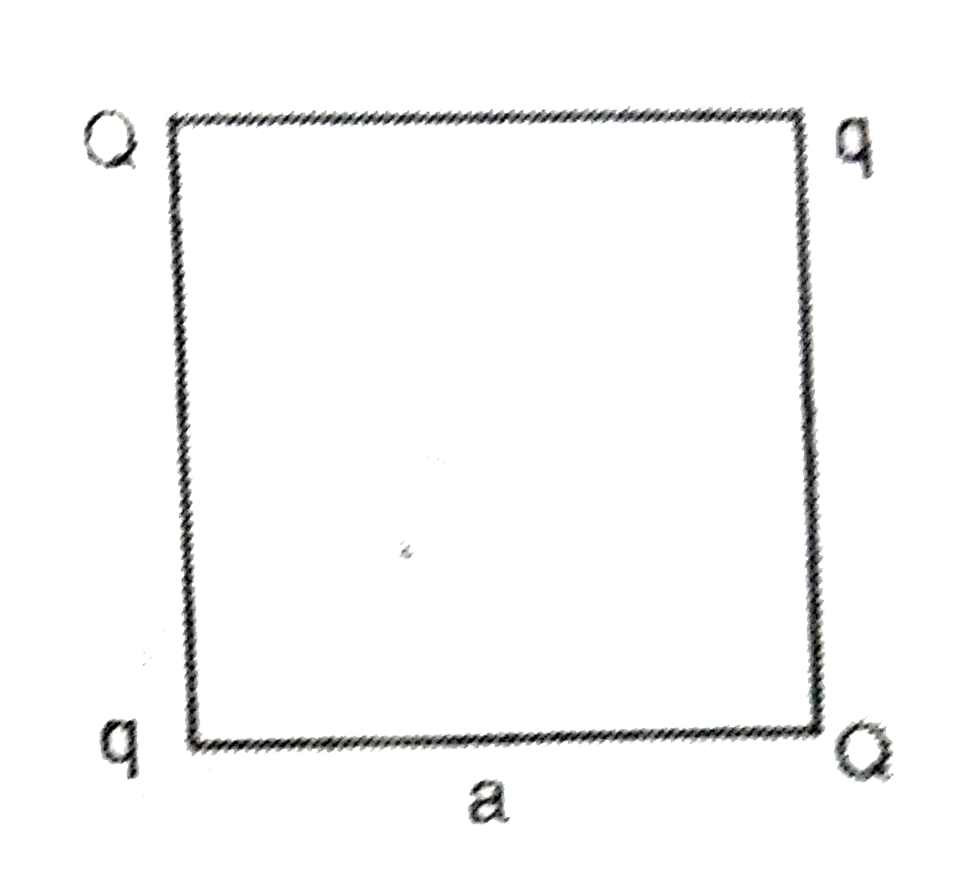
View SolutionFour point charges Q, q, Q and q are placed at the corners of a square of side' a' as shown in the figure.
Find the .
(a) resultnat electric force on a charge Q and .
(b) potential energy of this system.
View SolutionFour electric charges +q,+q,−q and −q are placed at the corners of a square of side 2L (see figure). The electric potential at point A, mid-way between the two charges +q and +q, is

View SolutionFour charges of same magnitude q are placed at four corners of a square of side a . The value electric potential at the centre of the souare will be (where k = 14πε0 )
View Solution