An infinitely long solid cylinder of radius R has a uniform vlume charge density ρ. It has a spherical cavity of radius R/2 with its center on the axis of the culinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R from the axis of the cylinder, is given by the expression 23ρR/16kε0. The value of k is

The correct Answer is:6
Volume of cylinder per unit length (l=1) is V=πR21=(πR)2
∴ Charge per unit length ,
λ = (volume per unit length) × ( volume charge density ) =(πR2ρ)
Now at P Er=ET−RC .
Remaining portion, Total proton and, Cavity
∴ ER=λ2πε0(2R)−14πε0R, Q = charge on sphere =43π(R2)3ρπR3ρ6
Substituing the vlaue , where value we have ER=(πR2ρ)4πε0R−14πε0R(πR3ρ/6)4R2=23ρp96ε0=23ρR(16)(6)ε0. ∴k=6
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE MAIN65videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT EXERCISE - IMPECCABLE52videos
ELECTROMAGNETIC INDUCTION & ALTERNATIVE CURRENT
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - TRUE/FALSE TYPE1videos
ENERGY & MOMENTUM
Similar Questions
An infinitely long solid cylinder of radius R has a uniform volume charge density ρ. It has a spherical cavity of radius R/2 with its centre on the axis of cylinder, as shown in the figure. The magnitude of the electric field at the point P, which is at a distance 2R form the axis of the cylinder, is given by the expression 23rR16ke0 . The value of k is .
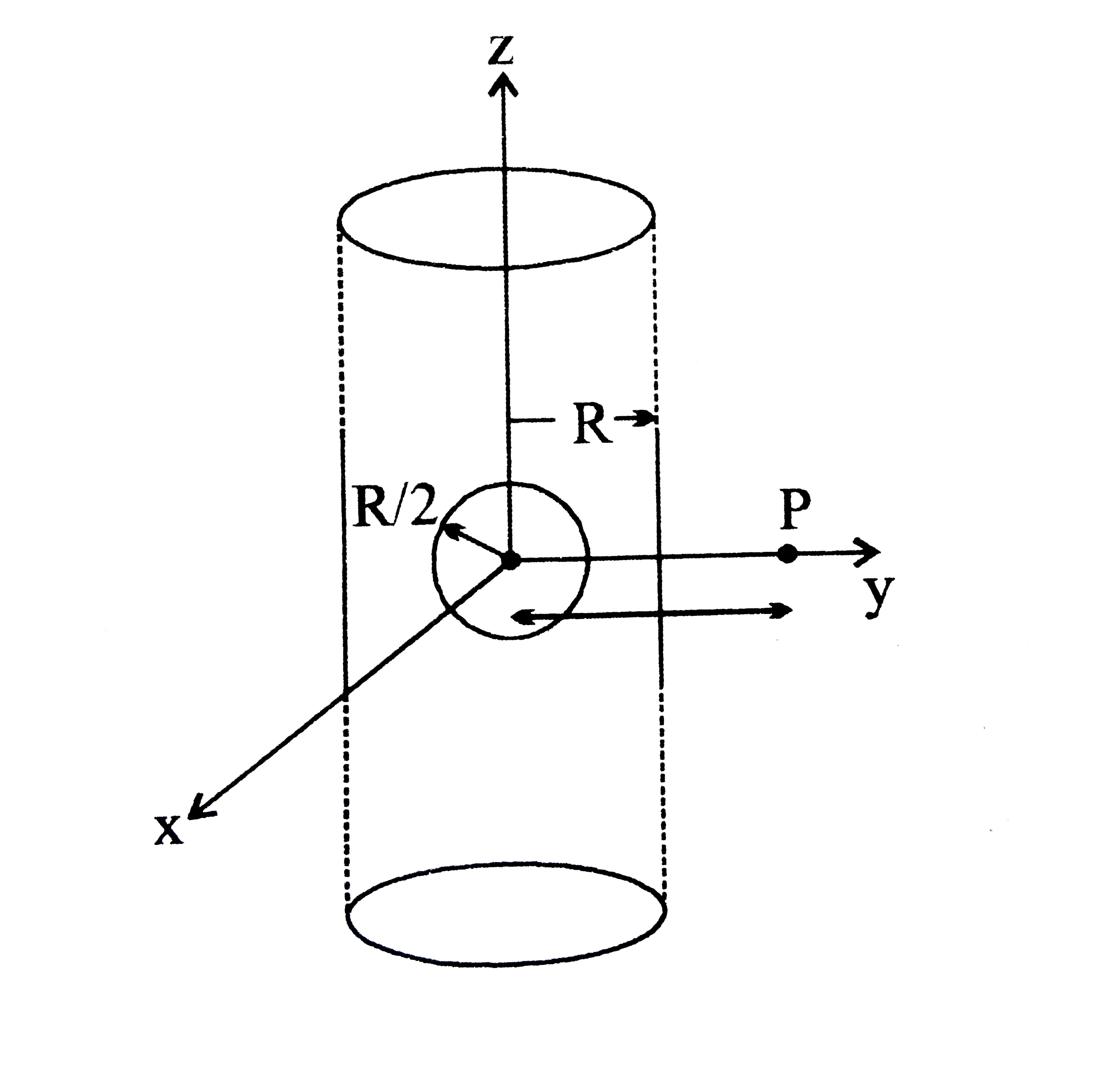 .View Solution
.View SolutionInside a uniformly charged infinitely long cylinder of radius 'R' and volume charge density 'rho' there is a spherical cavity of radius 'R//2'. A point 'P' is located at a dsintance 2R from the axis of the cylinder as shown. Then the electric field strength at the point 'P' is
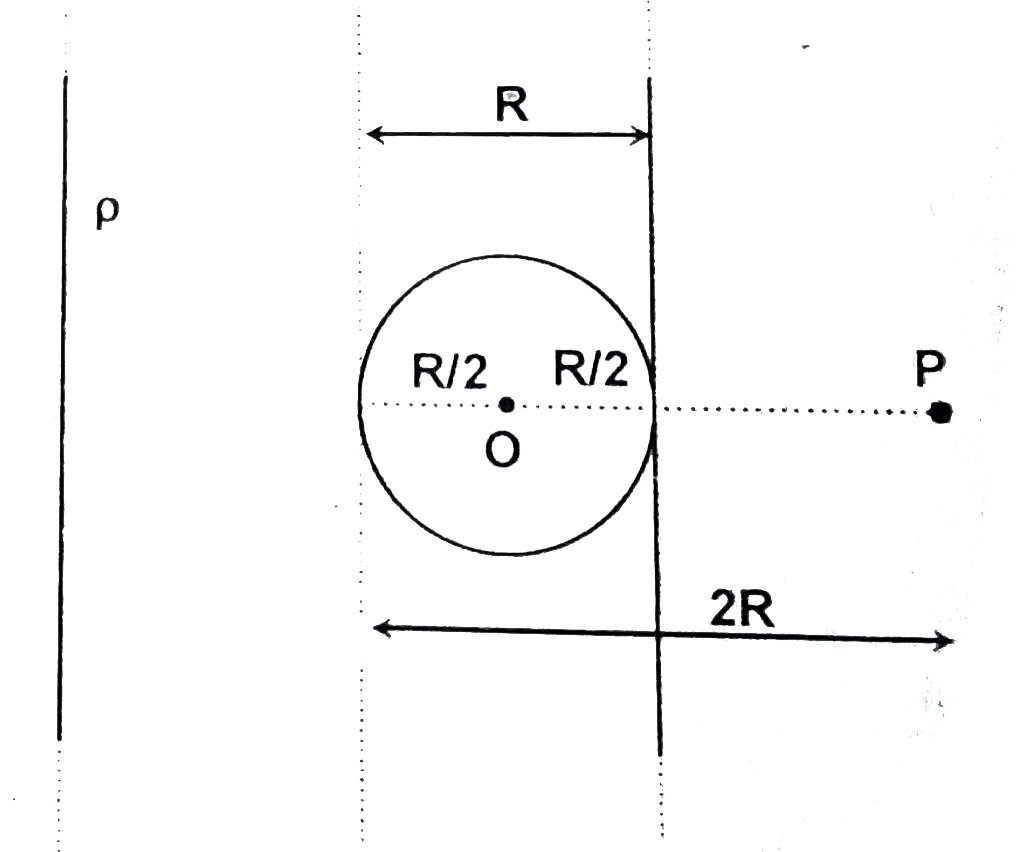 View Solution
View SolutionA solid of radius 'R' is uniformly charged with charge density ρ in its volume. A spherical cavity of radius R2 is made in the sphere as shown in the figure. Find the electric potential at the centre of the sphere.
 View Solution
View SolutionA solid sphere having radius R and uniform charge density ρ has a cavity of radius R2 as shown in figure.Find the value of ∣∣∣EAEB∣∣∣
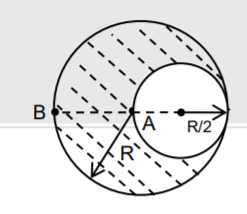 View Solution
View Solution
An infinity long cylinder of radius R has an infinitely long cylindrical cavity of radius R2 are shown in the figure. The remaining portion has uniform volume charge density ρ. The magnitude of electrical field at the centre of the cavity is-View SolutionA thick shell with inner radius R and outer radius 3R has a uniform charge density σc/m3. It has a spherical cavity of radius R as shown in the figure. The electric field at the centre of the cavity is
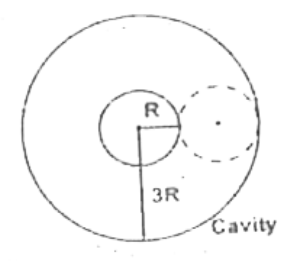 View Solution
View SolutionThe electric potential due to uniformly charged sphere of radius R,having volume charge density rho having a spherical cavity of radius R2 as shown as in figure at point p is
_PHY_E05_288_Q01.png) View Solution
View SolutionA positively charge sphere of radius r0 carries a volume charge density ρ. A spherical cavity of radius r0/2 is then scooped out and left empty. C1 is the center of the sphere and C2 that of the cavity. What is the direction and magnitude of the electric field at point B?
 View Solution
View SolutionA sphere of radius 2R and mas M has a spherical cavity of radius R as shown in the figure. Find the value of gravitational field at a point P at a distance of 6R from centre of the sphere.
 View Solution
View SolutionA long thin flat sheet has a uniform surface charge density σ. The magnitude of the electric field at a distance .r. from it is given by
View Solution
