Question

The figure shows a system consisting of (i) a ring of outer radius $3R$ rolling clockwise without slipping on a horizontal surface with angular speed co and (ii) an inner disc of radius $2R$ rotating anti-clockwise with angular speed $\omega /2$. The ring and disc are separated by frictionless ball bearings. The system is in the $x-z$ plane. The point $P$ on the inner disc is at distance $R$ from the origin, where $OP$ makes an angled of ${30}^{\circ }$ with the horizontal. Then with respect to the horizontal surface,

Options

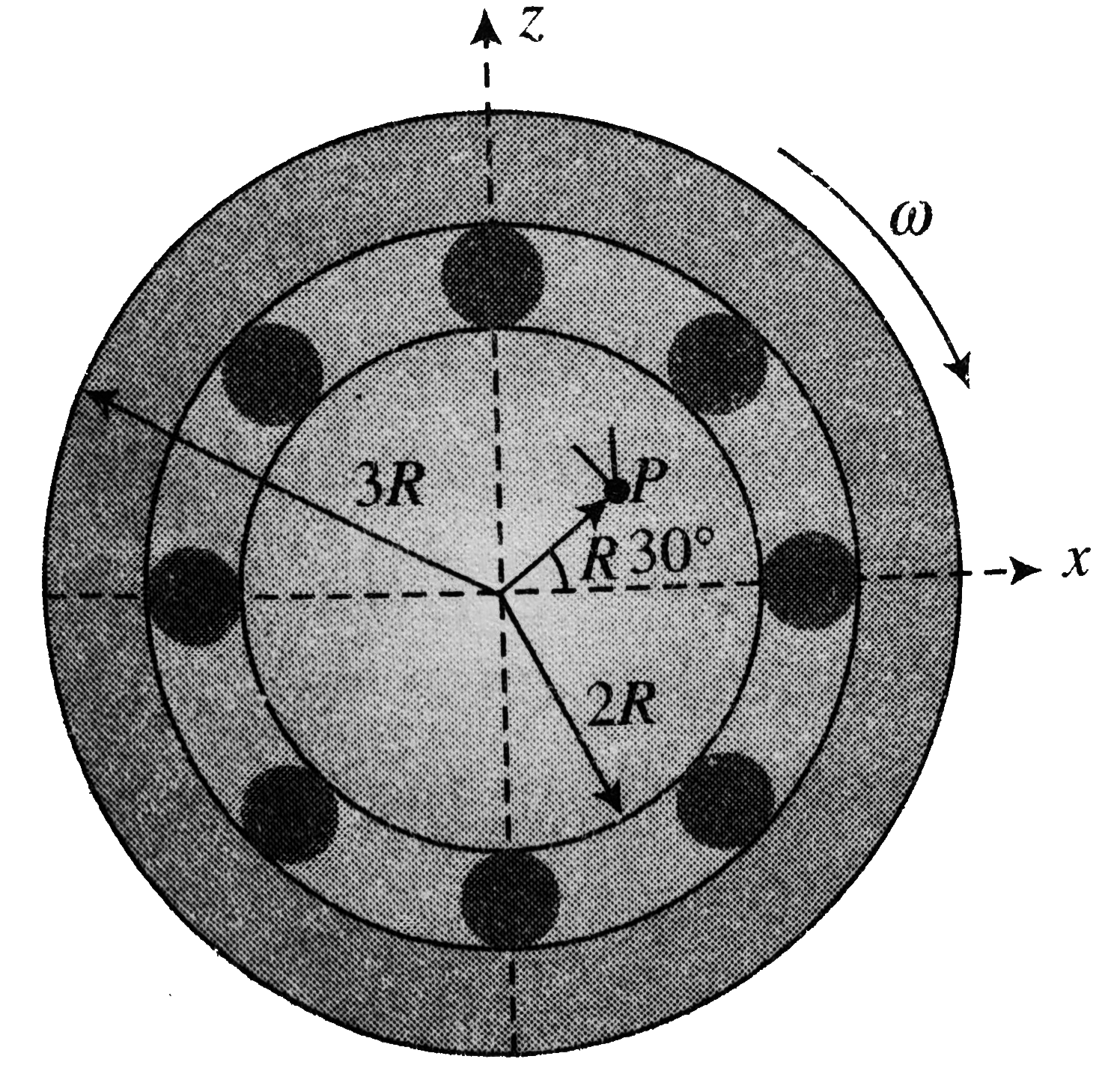
A. The point O has a linear velocity `3R omega hati`
B. The point P has a linear velocity `11/4 R omega hati + sqrt(3)/4 R omega hatk`
C. the point P has a liner velocity `13/4 R omega hati + sqrt(3)/4 R omega hatk`
D. The point P has a linear velocity `(3-sqrt(3)/4) R omega hati + 1/4 R omega hatk`

Answer

A::B

Explanation

As ring is rolling the point of contact of ring with ground (O') will be instantaneous centre of rotation. Hence for pure rolling and its direction is along positive x.
The velocity at the point P

`V_(P) = 3R omega hati - (Romega)/2 sin 30^(@) hati + (R omega)/2 cos 30^(@) hatk`
`v_(p) = 11/4 R omega hati + sqrt(3)/4 R omega hatk`