The potential energy of a particle of mass ? at a distance ? from a fixed point ? is given by V(r)=kr2/2, where ? is a positive constant of appropriate dimensions. This particle is moving in a circular orbit of radius ? about the point ?. If ? is the speed of the particle and ? is the magnitude of its angular momentum about ?, which of the following statements is (are) true?
v=√k2mR
v=√kmR
L=√mkR2
L=√mk2R2
The correct Answer is:B, C
To solve the problem step by step, we will analyze the potential energy given, derive the necessary expressions for the motion of the particle, and then evaluate the statements regarding the speed and angular momentum.
Step 1: Understand the Potential Energy Function
The potential energy V(r) of the particle is given by:
V(r)=kr22
where k is a positive constant and r is the distance from the fixed point.
Hint: The potential energy function indicates that the force acting on the particle is derived from this potential energy.
Step 2: Calculate the Force from Potential Energy
The force F acting on the particle can be found using the relation:
F=−dVdr
Calculating the derivative:
F=−ddr(kr22)=−kr
This force acts towards the center of the circular orbit, indicating that it is a restoring force.
Hint: Remember that the negative sign indicates that the force is attractive towards the center.
Step 3: Apply the Centripetal Force Condition
For a particle moving in a circular orbit, the centripetal force required to keep the particle in circular motion is given by:
Fcentripetal=mv2r
Setting the centripetal force equal to the force derived from the potential energy:
kr=mv2r
Multiplying both sides by r:
kr2=mv2
Hint: This equation relates the force acting on the particle to its mass and velocity.
Step 4: Solve for the Speed v
From the equation kr2=mv2, we can solve for the speed v:
v2=kr2m
Taking the square root gives:
v=√kr2m=r√km
Hint: This expression shows how the speed depends on the radius and the constants k and m.
Step 5: Calculate the Angular Momentum L
The angular momentum L of the particle about the center is given by:
L=mvr
Substituting the expression for v:
L=m(r√km)r=mr2√km
Simplifying this gives:
L=r2√km
Hint: Angular momentum is a measure of the rotational motion of the particle.
Conclusion
We have derived the expressions for speed v and angular momentum L:
- Speed: v=r√km
- Angular Momentum: L=r2√km
Now, we can evaluate which statements regarding these quantities are true based on the derived equations.
The potential energy V(r) of the particle is given by:
V(r)=kr22
where k is a positive constant and r is the distance from the fixed point.
The force F acting on the particle can be found using the relation:
F=−dVdr
Calculating the derivative:
F=−ddr(kr22)=−kr
This force acts towards the center of the circular orbit, indicating that it is a restoring force.
For a particle moving in a circular orbit, the centripetal force required to keep the particle in circular motion is given by:
Fcentripetal=mv2r
Setting the centripetal force equal to the force derived from the potential energy:
kr=mv2r
Multiplying both sides by r:
kr2=mv2
From the equation kr2=mv2, we can solve for the speed v:
v2=kr2m
Taking the square root gives:
v=√kr2m=r√km
The angular momentum L of the particle about the center is given by:
L=mvr
Substituting the expression for v:
L=m(r√km)r=mr2√km
Simplifying this gives:
L=r2√km
We have derived the expressions for speed v and angular momentum L:
- Speed: v=r√km
- Angular Momentum: L=r2√km
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (LINKED COMPREHENSIVE TYPE)
7 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (ASSERTION & REASON TYPE)
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
26 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
The potential energy of a particle varies with distance x from a fixed origin as V=A√XX+B where A and B are constants . The dimension of AB are
View SolutionA particle of charge 'q' and mass 'm' move in a circular orbit of radius 'r' with frequency 'v' the ratio of the magnetic moment to angular momentum is:
View Solution
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.A particle of charge q and mass m moves in a circular orbit of radius r with angular speed w the ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
Aw and qBw, q and mCq and mDw and m
Two particle A and B are moving as shown in the figure
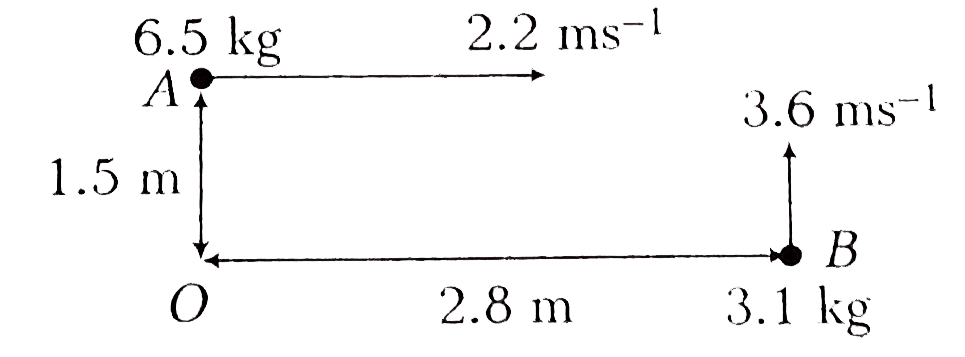
Their total angular momentum about the point O is
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of charge q and mass m moves in a circular orbit of radius r with angular speed ω. The ratio of the magnitude of its magnetic moment to that of its angular momentum depends on
View SolutionA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View SolutionA particle of mass m is being circulated on a vertical circle of radius r. If the speed of particle at the highest point be v, then
View SolutionCentripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?
View Solution
