A solid sphere is in pure rolling motion on an inclined surface having inclination θ
frictional force acting on sphere is f=μngcosθ
f is dissipative force
friction will increase its angular velocity and decrease its linear velocity
If θ decreases, friction will decreases.
The correct Answer is:C, D
In case of pure rolling.
f=mgsinθ1+mR2I (upwards) ∴f∝sinθ
Therefore, as θ decreases force of friction will also decreases.
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (LINKED COMPREHENSIVE TYPE)
7 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (ASSERTION & REASON TYPE)
2 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
26 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A solid sphere of mass m rolls without slipping on an inclined plane of inclination θ. The linear acceleration of the sphere is
View SolutionWhat is the minimum coefficient of friction for a solid sphere to roll without slipping on an inclined plane of inclination θ ?
View SolutionA solid sphere of mass m rolls without slipping on an inlined plane of inclination 0. what shoul be the minimum coefficient of static feiction to support pure rolling?
View SolutionA solid cylinder is rolling without slipping on a plane having inclination θ and the coefficient of static friction μs. The relation between θ and μs is
View SolutionA solid sphere is rolling on a frictionless surface, shown in figure with a translational velocity vm/s. If it is to climb the inclined surface then v should be :
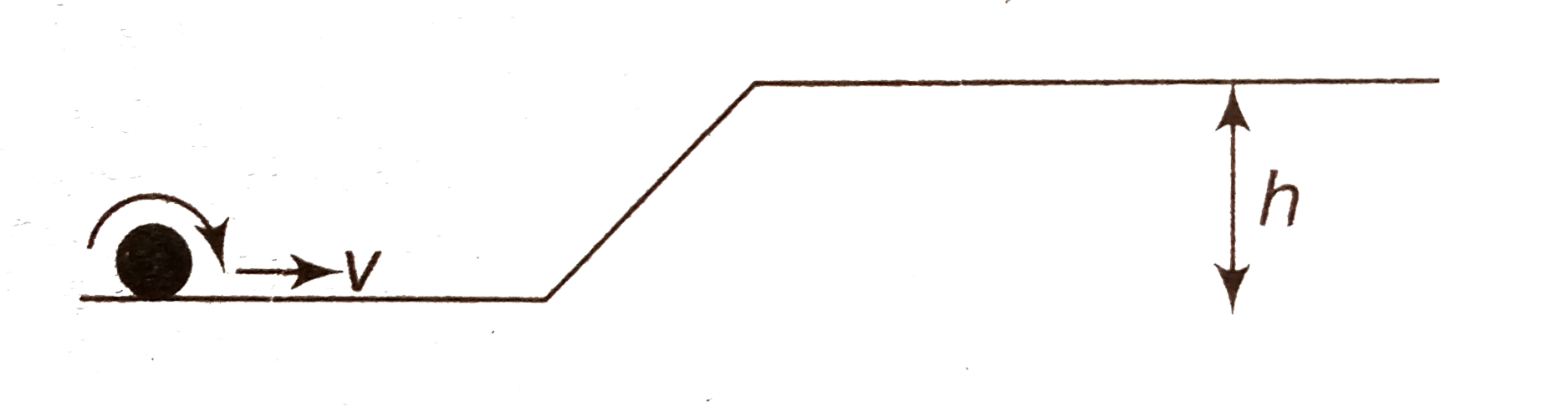
View SolutionA disc of radius R is rolling down an inclined plane whose angle of inclination is θ Its acceleration would be
View SolutionA solid cylinder of radius r rolls down an inclined plane of height h and inclination θ. Calculate its speed at the bottom of the plane using energy method. Also calculate the time taken to reach of the bottom.
View SolutionA sphere of mass m rolls without slipping on an inclined plane of inclination θ. Find the linear acceleration of the sphere and the force of friction acting on it. What should be the minimum coefficient of static friction to support pure rolling?
View SolutionA rolling object rolls without slipping down an inclined plane (angle of inclination θ), then the minimum acceleration it can have is ?
View SolutionThe velocity of a sphere rolling down an inclined plane of height h at an inclination θ with the horizontal, will be :
View Solution
