A uniform rod of length 6a and mass 8m lies on a smooth horizontal table. Two particle of masses m and 2m , moving in the same horizontal plane but in opposite directions with speeds 2v and v respectively strike and rod normally as shown in figure and stick to the rod. Denoting angular velocity ( about the centre of mass), total energy and transnational velocity of centre of mass by ω, E and vc respectively after the collision.
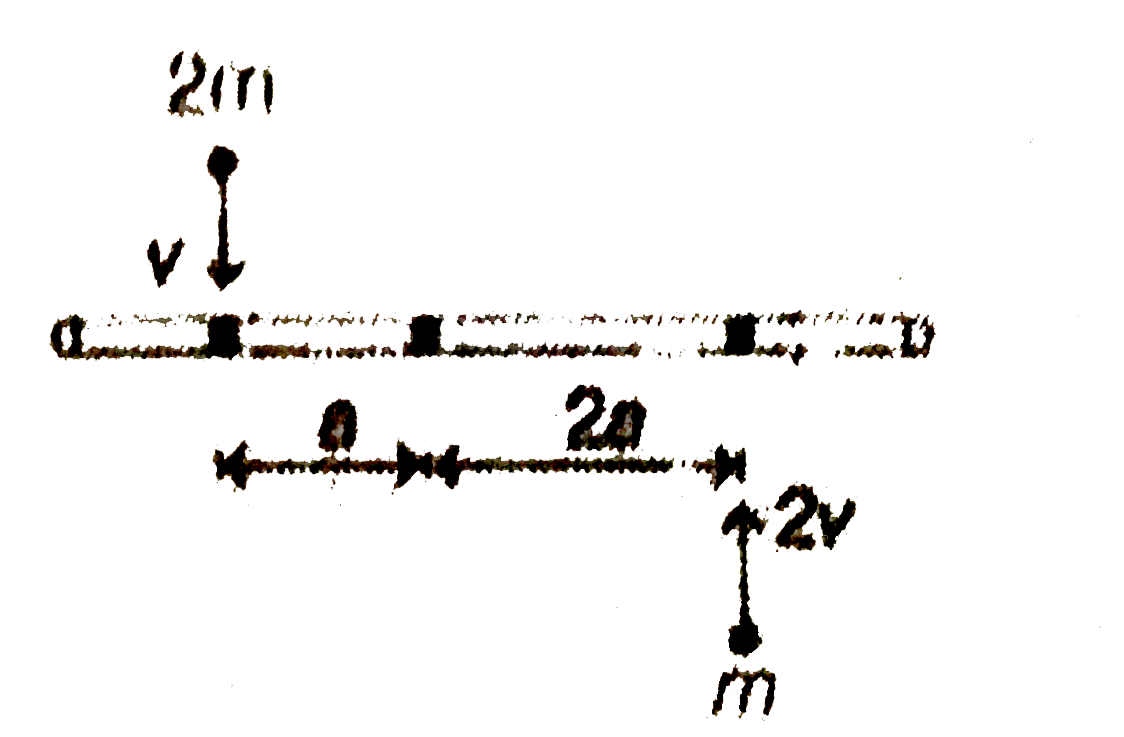
Vc=0
ω=3v5a
ω=v5a
E=3mv25
The correct Answer is:A, C, D
Net external force on the system is zero. Therefore, linear momentum will remain conserved. Initially both the particles have equal momentum in opposite direction. Hence, initial momentum is zero i.e., final linear momentum is also zero or velocity of centre of mass vc=0
Let be the angular velocity about centre of mass. Net external torque on system is also zero. Hence, angular momentum about centre of mass will also be conserved , i.e. Li=Lg
or (2mva4mva)=Iω={8m(6a)212+(2m)(s)2+m(2a)2}ω or 6mva=(24ma2+2ma2+4ma2)ω=(30ma2)ω or ω=v5a
Finally, E=12Iω2=12(30ma2)(v5a)2=35mv2
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE MAIN (ARCHIVE)
58 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
26 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (General rigid body motion, Rolling)
10 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
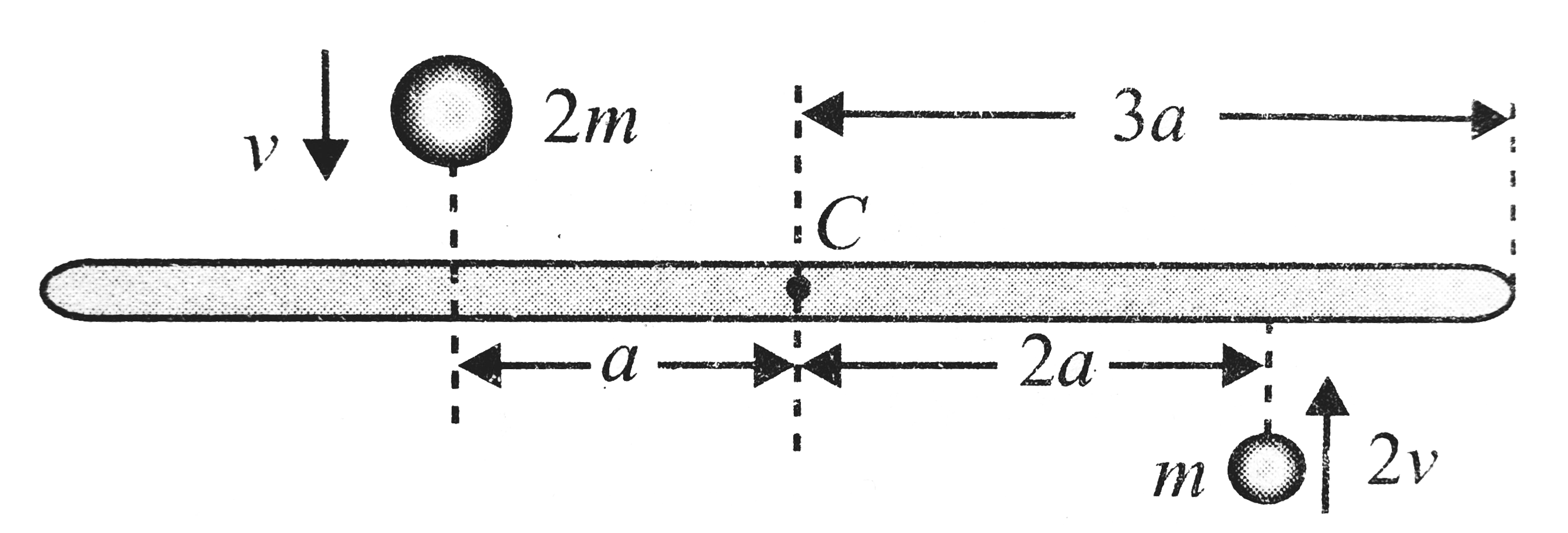
A uniform bar of length 6a and mass 8m lies on a smooth horizontal table. Two point masses m and 2m moving in the same horizontal plane with speeds 2v and v, respectively, strike the bar (as shown in the figure) and stick to the bar after collision. Denoting angular velocity (about the centre of mass), total energy and centre of mass velocity by ω, E and VC, respectively, we have after collision
View SolutionA uniform rod of length 8 a and mass 6 m lies on a smooth horizontal surface. Two point masses m and 2 m moving in the same plane with speed 2 v and v respectively strike the rod perpendicular at distances a and 2a from the mid point of the rod in the opposite directions and stick to the rod. The angular velocity of the system immediately after the collision is
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
View SolutionA uniform rod of length l and mass 2 m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with velocity v collides with one end of the rod and sticks it. Then
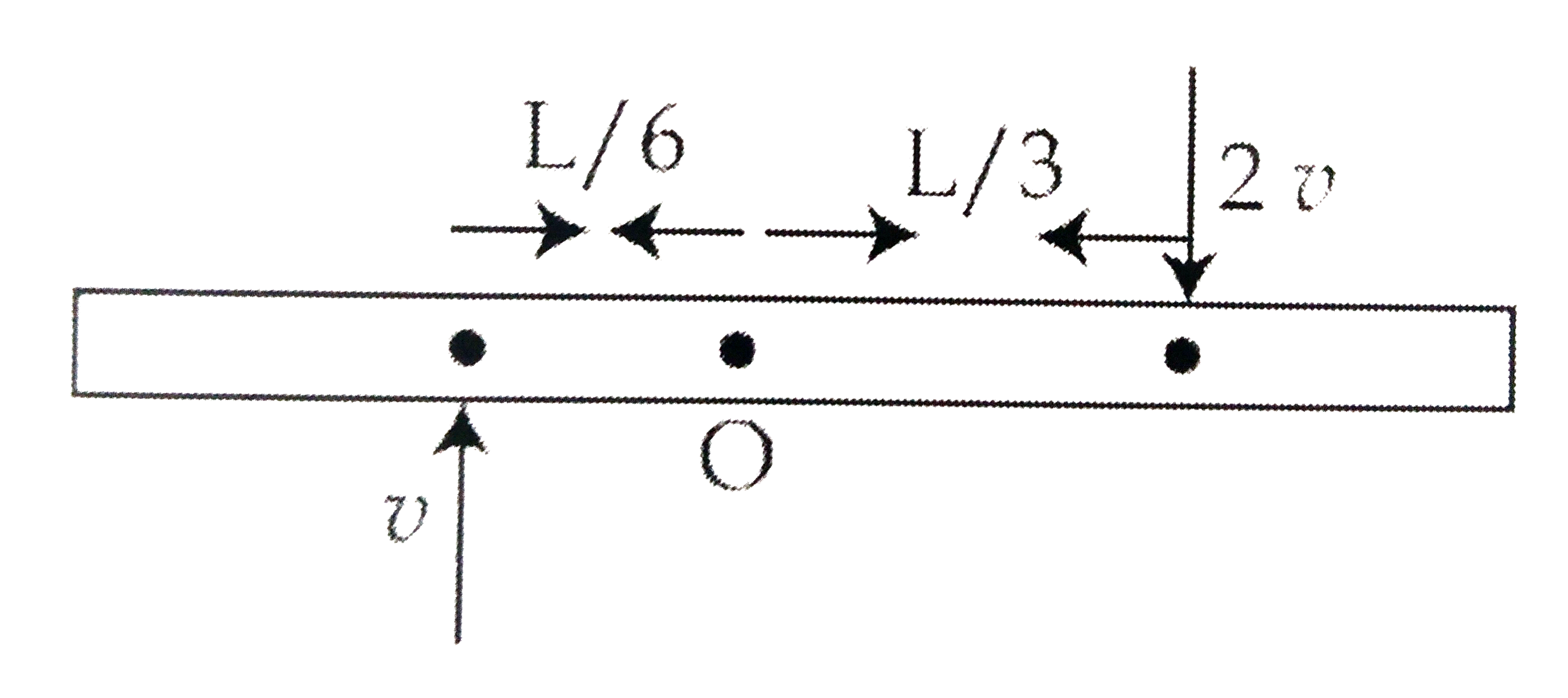
View SolutionA thin uniform bar of length L and mass 8m lies on a smooth horizontal table .Two point masses m and 2 m are moving in the same horizontal plane from opposite sides of the bar with speeds 2v and v respectively .The masses stick to the bar after collision at a distances L3andL6 respectively from the center of the bar if the bar starts rotating about its center of mass as result of collision the angular speed of the bar will be
View SolutionTwo particles of masses m and 2m moving in opposite directions collide elastically with velocity 2v and v, respectiely. Find their velocities after collision.

View SolutionTwo particles of mass 1 kg and 0.5 kg are moving in the same direction with speed of 2m/s and 6 m/s respectively on a smooth horizontal surface. The speed of centre of mass of the system is
View SolutionA uniform rod of length l and mass 2m rests on a smooth horizontal table. A point mass m moving horizontally at right angles to the rod with initial velocity v collides with one end of the rod and sticks to it.
Determine the position of the point on the rod which remains stationary immediately after collision.
View SolutionA uniform rod of mass M and length a lies on a smooth horizontal plane. A particle of mass m moving at a speed v perpendicular to the length of the rod strikes it at a distance a4 from the centre and stops after the collision. Find a. the velocity of the cente of the rod and b. the angular velocity of the rod abut its centre just after the collision.
View SolutionA rod AB of length 2L and mass m is lying on a horizontal frictionless surface. A particle of same mass m travelling along the surface hits the rod at distance L2 from COM with a velocity v0 in a direction perpendicular to rod and sticks to it.
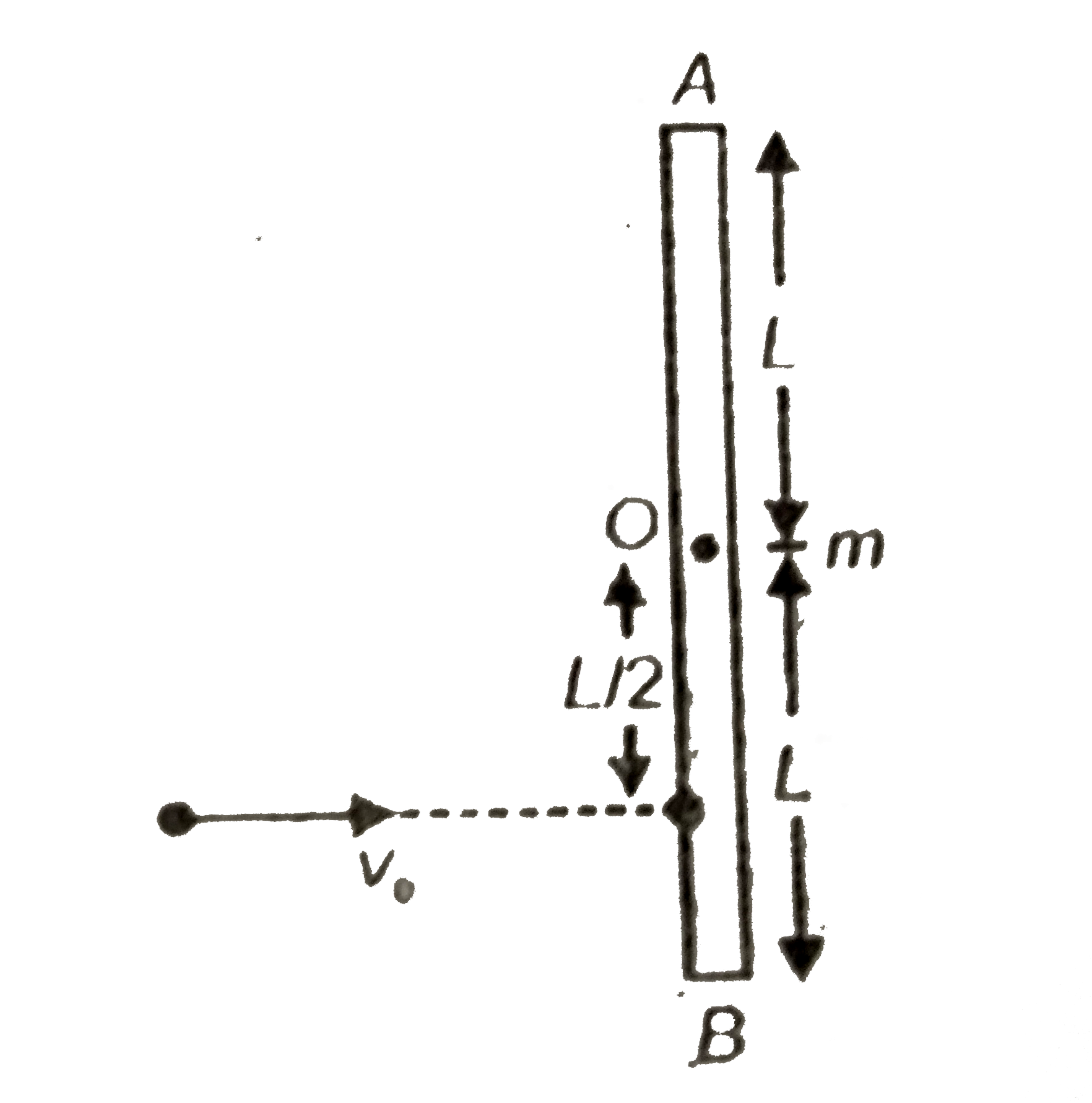
Angular velocity of rod just after collision is
View Solution
