
A solid sphere of mass m and radius R is gently placed on a conveyer belt moving with constant velocity v0. If coefficient of friction between belt and sphere is 2/7 the distance traveled by the centre of the sphere before it starts pure rolling is
v207g
2v2049g
2v205g
2v207g
The correct Answer is:A
Nμ=ma⇒a=gμ⇒NμR=23mR2α⇒5gμ2Rv=gμt,ω=5gμ2Rt
Pure rolling starts when v+Rω=v0
⇒gμt+52gμt=v0⇒t=2v07gμ

s=12at2=12gμ4v2049g2μ2=2v2049gμ⇒s=2v2049g(2/7)v207g
Topper's Solved these Questions
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE MAIN (ARCHIVE)
58 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - JEE Advanced (Archive) (SINGLE OPTION CORRECT TYPE)
26 Videos
- ROTATIONAL MOTION BOOK - VMC MODULES ENGLISHCHAPTER - ROTATIONAL MOTION EXERCISE - LEVEL - 2 (General rigid body motion, Rolling)
10 Videos
- REVISION TEST-2 JEEBOOK - VMC MODULES ENGLISHCHAPTER - REVISION TEST-2 JEEEXERCISE - PHYSICS
25 Videos
- SIMPLE HARMONIC MOTION BOOK - VMC MODULES ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - 7-previous year question
46 Videos
Similar Questions
A hollow sphere of mass m and radius R is rolling downdard on a rough inclined plane of inclination θ. If the coefficient of friction between the hollow sphere and incline is μ, then
View Solution
A horizontal plank having mass m lies on a smooth horizontal surface. A sphere of same mass and radius r is spined to angular frequency ω0 and gently placed on the plank as shown in the figure. If coefficient of friction between the plank and the sphere is μ. Find the distance moved by the plank till sphere starts pure rolling on the plank. the plank is long enough.
View SolutionA sphere of mass m and radius r is projected in a gravity free space with speed v. If coefficient of viscosity of the medium in which it moves is 16π , the distance travelled by the body before it stops is
View SolutionA sphere of mass m and radius r is projected in a gravity free space with speed v. If coefficient of viscosity of the medium in which it moves is 16π , the distance travelled by the body before it stops is
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.

Find the displacement of the plank till the sphere starts pure rolling.
View SolutionA long horizontal plank of mass m is lying on a smooth horizontal surface. A sphere of same mass m and radius r is spinned about its own axis with angular velocity we and gently placed on the plank. The coefficient of friction between the plank and the sphere is μ. After some time the pure rolling of the sphere on the plank will start. Answer the following questions.
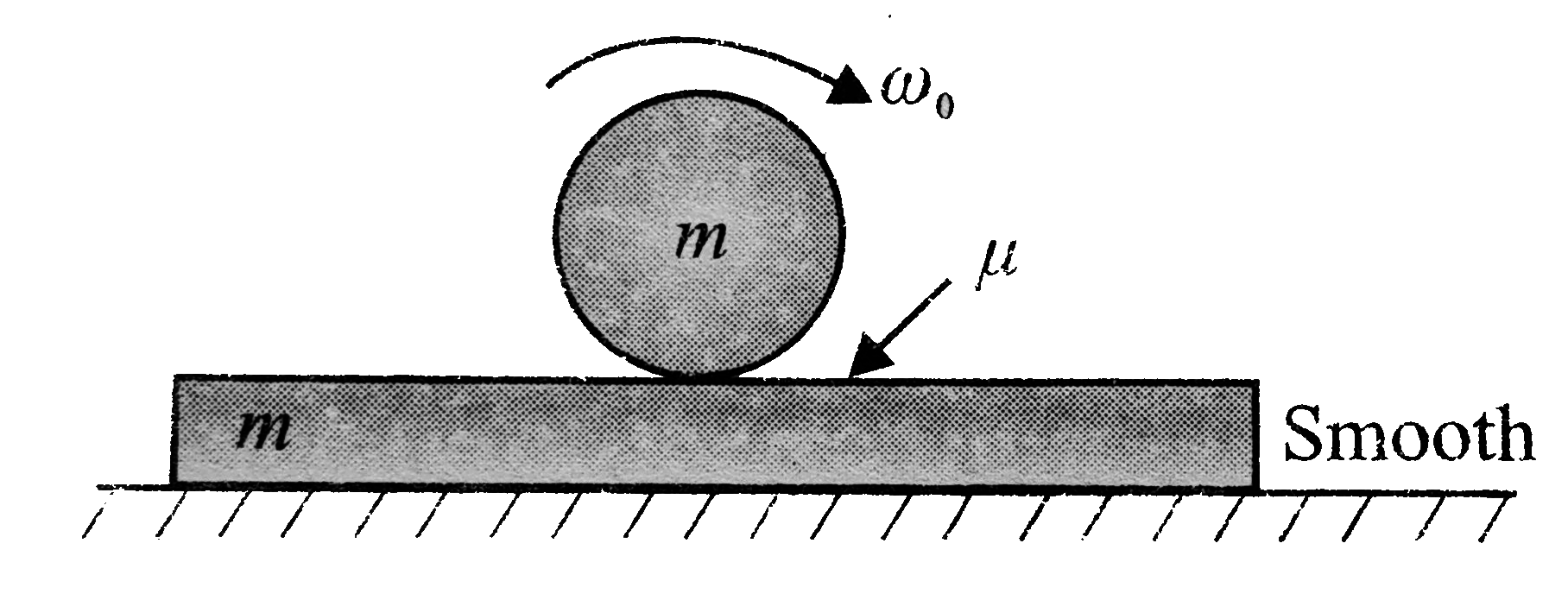
Find the time t at which the pure roiling starts
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.
Angular acceleration of sphere is
View SolutionAssertion : A solid and a hollow sphere both of equal masses and radii are put on a rough surface after rotating with some angular velocity say ω0. Coefficient of friction for both the spheres and ground is same. Solid sphere will start pure rolling first
Reason : Radius of gyration of hollow sphere about an axis passing through its centre of mass is more.
View SolutionA solid sphere of mass m and radius R is placed over a plank of same mass m. There is sufficient friction between sphere and plank to prevent slipping.When a horizontal force F is applied at centre of sphere, acceleration of the plank is

View SolutionA suitcase is gently dropped on a conveyor belt moving at 3m/s. If the coefficient of friction between the belt and the suitcase is 0.5. Find the displacement of suitcase relative to conveyor belt before the slipping between the two is stopped (g=10m/s2)
View Solution
