A 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
0.05Vm−1
0.5Vm−1
0.01Vm−1
0.1Vm−1
To solve the problem step by step, we will calculate the potential gradient of the potentiometer wire connected in series with a battery and a resistor.
Step 1: Identify the given values
- Voltage of the battery (V) = 2 V
- Resistance of the fixed resistor (R1) = 990 Ω
- Resistance of the potentiometer wire (R2) = 10 Ω
- Length of the potentiometer wire (L) = 2 m
Step 2: Calculate the total resistance in the circuit
Since the resistor and the potentiometer are connected in series, the total resistance (R_eq) can be calculated as:
Req=R1+R2
Substituting the values:
Req=990Ω+10Ω=1000Ω
Step 3: Calculate the current flowing through the circuit
Using Ohm's law, the current (I) flowing through the circuit can be calculated as:
I=VReq
Substituting the values:
I=2V1000Ω=0.002A=2×10−3A
Step 4: Calculate the potential drop across the potentiometer wire
The potential drop (E) across the potentiometer wire can be calculated using:
E=I×R2
Substituting the values:
E=(2×10−3A)×(10Ω)=2×10−2V
Step 5: Calculate the potential gradient of the potentiometer wire
The potential gradient (E/L) can be calculated as:
Potential Gradient=EL
Substituting the values:
Potential Gradient=2×10−2V2m=0.01V/m
Final Answer
The potential gradient of the potentiometer wire is 0.01 V/m.
---
- Voltage of the battery (V) = 2 V
- Resistance of the fixed resistor (R1) = 990 Ω
- Resistance of the potentiometer wire (R2) = 10 Ω
- Length of the potentiometer wire (L) = 2 m
Since the resistor and the potentiometer are connected in series, the total resistance (R_eq) can be calculated as:
Req=R1+R2
Substituting the values:
Req=990Ω+10Ω=1000Ω
Using Ohm's law, the current (I) flowing through the circuit can be calculated as:
I=VReq
Substituting the values:
I=2V1000Ω=0.002A=2×10−3A
The potential drop (E) across the potentiometer wire can be calculated using:
E=I×R2
Substituting the values:
E=(2×10−3A)×(10Ω)=2×10−2V
The potential gradient (E/L) can be calculated as:
Potential Gradient=EL
Substituting the values:
Potential Gradient=2×10−2V2m=0.01V/m
The potential gradient of the potentiometer wire is 0.01 V/m.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-4
15 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET -5
15 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-2
15 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
Potentiometer wire of length 1m is connected in series with 490Ω resistance and 2V battery. If 0.2mVcm is the potential gradient, then resistance of the potentiameter wire is approximately
View SolutionPotentiometer wire of length 1m is connected in series with 490Ω resistance and 2V battery. If 0.2mVcm is the potential gradient, then resistance of the potentiameter wire is approximately
View SolutionIn the primary circuit of a potentiometer, a cell of E.M.F 1 V and a rheostat of 15Ω are connected in series. If the resistance of the potentiometer wire is 10Ω the minimum voltage at the ends of the wire (in V) will be
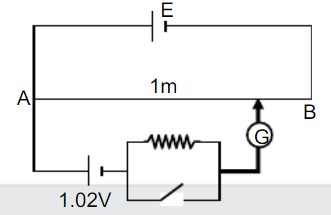
View SolutionIn given potentiometer circuit 1.02V is balanced at 5.1cm from A. Find potential gradient of potentiometer wire AB:
View SolutionA 10 m long uniform metallic wire having a resistance of 20Ω is used as a potentiometer wire. This wire is connected in series with another resistance of 480Ω and a battery of emf 5 V having negligible internal resistance. If an unknown emf e is balanced across 6 m of the potentiometer wire, calculate :
the potential gradient across the potentiometer wire.
View SolutionThe balancing length for a cell in a potentiometer experiment is 45 cm. In the balanced condition, the current through the potentiometer wire is 2 A. If the total length of the potentiometer wire is 1 m and its total resistance is60Ω , the emf of the cell is (in Volts) _________.
View SolutionA potentiometer consists of a wire of length 4 m and resistance 10Ω. It is connected to a cell of emf 2V.The potential gradient of the wire is
View SolutionA 10 m along uniform metallic wire having a resistance of 20Ω is used as a potentiometer wire. This wire is connected in series with another resistance of 480Ω and a battery of emf 5 V having negligible internal resistance . If an unknown emf e is balanced across 6 m of the potentiometer wire. Calculate :
(i) The potential gradient across the potentiometer wire.
(ii) the value of the unknown emf e.
View SolutionThe wire of potentiometer has resistance 4Ω and length 1m. It is connected to a cell of e.m.f. 2V and internal resistance 1Ω. The current flowing through the potentiometer wire is
View SolutionIn a potentiometer wire experiment the emf of a battery in the primary circuit is 20V and its internal resistance is 5Ω. There is a resistance box in series with the battery and the potentiometer wire, whose resistance can be varied from 120Ω to 170Ω. Resistance of the potentiometer wire is 75Ω. The following potential differences can be measured using this potentiometer.
View Solution
