The balancing length for a cell in a potentiometer experiment is 45 cm. In the balanced condition, the current through the potentiometer wire is 2 A. If the total length of the potentiometer wire is 1 m and its total resistance is60Ω , the emf of the cell is (in Volts) _________.
To find the EMF of the cell in the potentiometer experiment, we will follow these steps:
Step 1: Understand the relationship between resistance and length
The resistance of the potentiometer wire is directly proportional to its length. Given that the total length of the potentiometer wire is 1 meter (100 cm) and its total resistance is 60 Ω, we can find the resistance per centimeter.
Step 2: Calculate the resistance per centimeter
The total resistance of the potentiometer wire is given as 60 Ω for 100 cm. Therefore, the resistance per centimeter (R_per_cm) can be calculated as follows:
Rper cm=60Ω100cm=0.6Ω/cm
Step 3: Calculate the resistance for the balancing length
The balancing length for the cell is given as 45 cm. We can find the resistance (R1) corresponding to this length:
R1=Rper cm×balancing length=0.6Ω/cm×45cm=27Ω
Step 4: Use Ohm's Law to find the EMF
The EMF (E) of the cell can be calculated using Ohm's Law, which states that:
E=I×R1
Where:
- I is the current through the potentiometer wire (2 A)
- R1 is the resistance corresponding to the balancing length (27 Ω)
Substituting the values:
E=2A×27Ω=54V
Conclusion
The EMF of the cell is 54 Volts.
---
The resistance of the potentiometer wire is directly proportional to its length. Given that the total length of the potentiometer wire is 1 meter (100 cm) and its total resistance is 60 Ω, we can find the resistance per centimeter.
The total resistance of the potentiometer wire is given as 60 Ω for 100 cm. Therefore, the resistance per centimeter (R_per_cm) can be calculated as follows:
The balancing length for the cell is given as 45 cm. We can find the resistance (R1) corresponding to this length:
The EMF (E) of the cell can be calculated using Ohm's Law, which states that:
- I is the current through the potentiometer wire (2 A)
- R1 is the resistance corresponding to the balancing length (27 Ω)
The EMF of the cell is 54 Volts.
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-1
Explore 10 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-2
Explore 10 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 DAILY TUTORIAL SHEET-4
Explore 15 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
If the resistance of potentiometer wire is 15r then calculate the balance length l
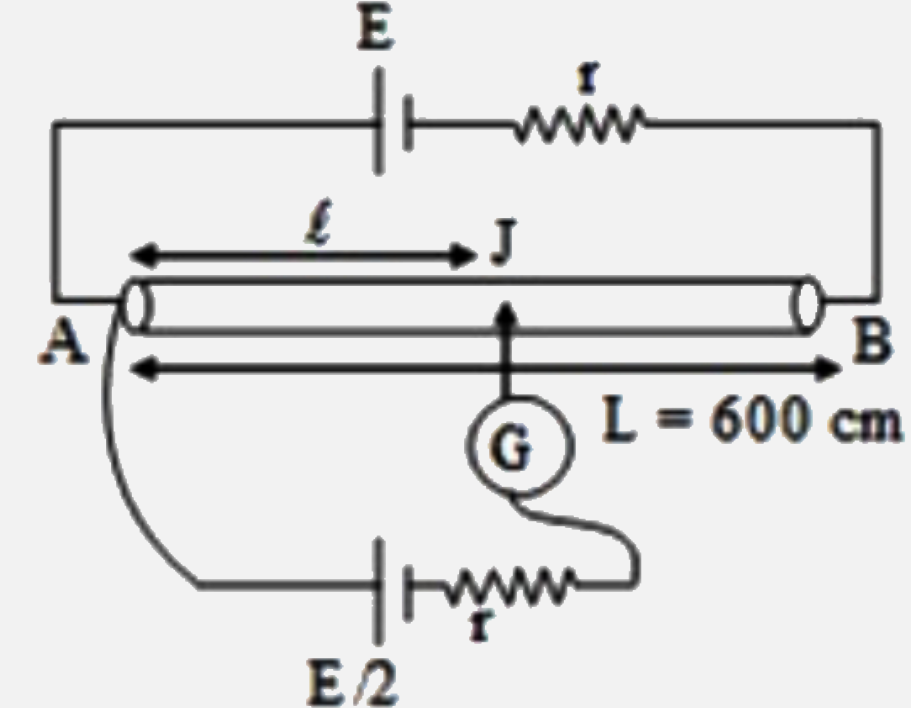
View SolutionA 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
View SolutionA 2 V battery, a 990Ω resistor and a potentiometer of 2 m length, all are connected in series of the resistance of potentiometer wire is 10Ω, then the potential gradient of the potentiometer wire is
View SolutionIn potentiometer experiment, null point isobtained at a particular point for a cell on potentiometer wire x cm long. If the lengthof the potentiometer wire is increasedwithout changing the cell, the balancing length will (Driving source is not changed)
View SolutionIf the balance length corresponding to points B and C is 40 cm on the potentiometer wire, the balance length corresponding to point C and D is
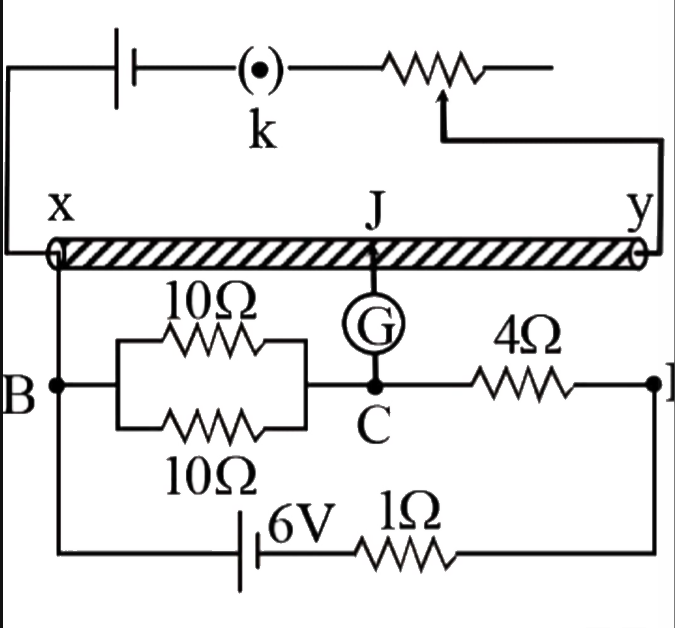
View SolutionAssertion : The e.m.f. of the drivercell in the potentiometer experiment should be greater than the e.m.f. of the cell to determined. reason ; the fall of potential across the potentiometer wire should not be less than the emf of the cell to be determined.
View SolutionIt is observed in a potentiometer experiment that no current passes through the galvanometer, when the terminals of the potentiometer, wire. On shunting the cell by a 2Ω resistance, the balancing length is reduced to half. The internal resistance of the cell is:-
View SolutionThe length of a potentiometer wire is l. A cell of emf E is balanced at a length l/3 from the positive end of the wire. If the length of the wire is increased by l/2. At what distance will the same cell give a balance point.
View SolutionIn a potentiometer experiment it is found that no current passes through the galvanometer when the terminals of the cell are connected across 0.52m of the potentiometer wire. If the cell is shunted by a resistance of 5Ω balance is obtained when the cell connected across0.4m of the wire. Find the internal resistance of the cell.
View SolutionIn a potentiometer experiment it is found that no current passes through the galvanometer when the terminals of the cell are connected across 0.52m of the potentiometer wire. If the cell is shunted by a resistance of 5Ω balance is obtained when the cell connected across0.4m of the wire. Find the internal resistance of the cell.
View Solution