A potential difference 100 V is applied across a conductor which is a cylindrical shell of inner and outer diameter 2 cm and 4 cm respectively and length 10 cm. Current flows in a direction parallel to the axis of the conductor. If heat is dissipated in the conductor at the rate 15 W, the resistivity of the material of the conductor is _________ Ωm. [Take π=228]
To solve the problem, we need to find the resistivity of the material of the cylindrical conductor given the potential difference, dimensions of the conductor, and the rate of heat dissipation.
1. Identify the Given Values:
- Potential difference (V) = 100 V
- Inner diameter (d1) = 2 cm = 0.02 m
- Outer diameter (d2) = 4 cm = 0.04 m
- Length of the conductor (L) = 10 cm = 0.1 m
- Heat dissipated (H) = 15 W
2. Calculate the Cross-Sectional Area (A) of the Cylindrical Shell:
- The cross-sectional area of the cylindrical shell can be calculated using the formula:
A=π4(d22−d21)
- Substitute the values:
A=22/74((0.04)2−(0.02)2)
A=22/74(0.0016−0.0004)=22/74×0.0012
A=22×0.001228=0.026428≈0.000942857 m2
3. Use the Heat Dissipation Formula:
- The heat dissipated in the conductor is given by:
H=V2R
- The resistance (R) can also be expressed in terms of resistivity (ρ):
R=ρLA
- Therefore, we can express heat as:
H=V2AρL
4. Rearranging to Find Resistivity (ρ):
- Rearranging the equation gives:
ρ=V2AHL
5. Substituting the Known Values:
- Substitute V = 100 V, A = 0.000942857 m², H = 15 W, and L = 0.1 m:
ρ=(100)2×0.00094285715×0.1
ρ=10000×0.0009428571.5
ρ=9.428571.5≈6.28571 Ωm
6. Final Answer:
- The resistivity of the material of the conductor is approximately 6.25 Ωm.
- Potential difference (V) = 100 V
- Inner diameter (d1) = 2 cm = 0.02 m
- Outer diameter (d2) = 4 cm = 0.04 m
- Length of the conductor (L) = 10 cm = 0.1 m
- Heat dissipated (H) = 15 W
- The cross-sectional area of the cylindrical shell can be calculated using the formula:
A=π4(d22−d21)
- Substitute the values:
A=22/74((0.04)2−(0.02)2)
A=22/74(0.0016−0.0004)=22/74×0.0012
A=22×0.001228=0.026428≈0.000942857 m2
- The heat dissipated in the conductor is given by:
H=V2R
- The resistance (R) can also be expressed in terms of resistivity (ρ):
R=ρLA
- Therefore, we can express heat as:
H=V2AρL
- Rearranging the equation gives:
ρ=V2AHL
- Substitute V = 100 V, A = 0.000942857 m², H = 15 W, and L = 0.1 m:
ρ=(100)2×0.00094285715×0.1
ρ=10000×0.0009428571.5
ρ=9.428571.5≈6.28571 Ωm
- The resistivity of the material of the conductor is approximately 6.25 Ωm.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-1
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-2 DAILY TUTORIAL SHEET-2
10 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-4
15 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
The length of a current-carrying cylindrical conductor is l, its area of cross-section is A, the number density of free electrons in it is n, and the drift velocity of electrons in it is vd . The number of electrons passing through a particular cross-section of the conductor per unit time is given by:
View SolutionEight cells marked 1 to 8, each of emf 5V and internal resistance 0.2Ω are connected as shown. What is the reading of ideal voltmeter ?
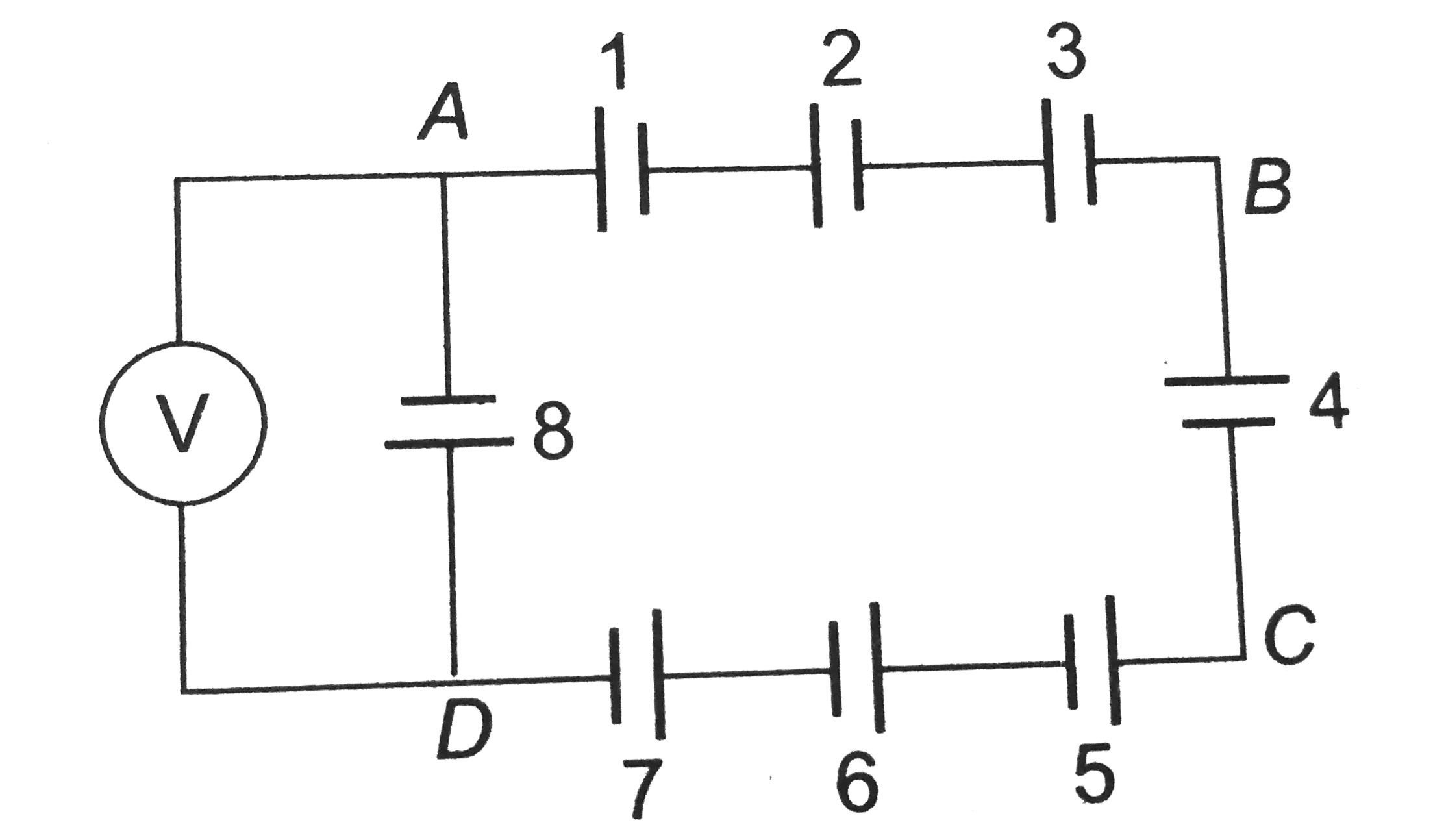
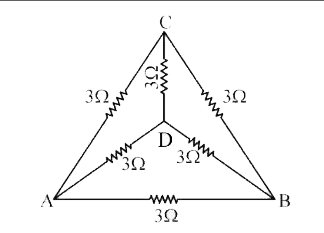
View SolutionThe equivalent resistance between A and B in the given circuit is:
View SolutionThree bulbs of 40 W , 60 W , 100 W are arranged in series with 220 volt supply which bulb has minimum resistance
View SolutionIf a ship of mass 4×107 kg initially at rest is pulled by a force of 5×104 N through a distance of 4 m, then the speed of the ship will be (resistance due to water is negligible )
View SolutionFind the resistance of a hollow cylindrical conductor of length 1.0m and inner and outer radii 1.0mm and 2.0mm respectively. The resistivity of the material is 2.0×10−8(Ω)m.
View SolutionA current of 0.2A flows through a conductor of resistance 4.5Ω. Calculate the potential difference at the ends of the conductor.
View SolutionA potential difference is applied between the ends of a conductor of uniform radius 2mm. It results in an electric field of strength 250V/m along the length of conductor. Find the resistivity of the material if current in the conductor is 2πA.
View SolutionA potential difference of 10 V is applied across a conductor of resistance 1kΩ. Find the number of electrons flowing through the conductor in 5 minutes.
View SolutionSpecific resistance of a metal conductor is 4xx10^(-5)Omega m and its area of cross section is 8 cm^(2) when 0.2A current passes through the conductor then potential gradient of the conductor is
View SolutionResistance of a conductor is 200Ω and the current through it is 10 mA,What is the potential difference across the two ends of the conductor?
View SolutionTwo resistances 1Ω and 2Ω are connected in parallel and a potential difference of 6V is applie across the ends this combination, Calculate the current through the second conductor.
View SolutionA potential difference of 3V is applied across a conductor through which 5A of current is flowing. Determine the resistance of the conductor.
View SolutionA potential difference 100 V is applied across a conductor which is a cylindrical shell of inner and outer diameter 2 cm and 4 cm respectively and length 10 cm. Current flows in a direction parallel to the axis of the conductor. If heat is dissipated in the conductor at the rate 15 W, the resistivity of the material of the conductor is _________ Omega m . [Take pi=22/8 ]
View SolutionA copper conductor is in the shape of a cylindrical shell of length 20 cm and inner and outer diameter 1 cm and 3 cm. A potential difference 200 V is applied between the flat surfaces of the conductor. The current density in it is 10A/m2 . The value of x is ________
View Solution
