Voltmeters V1andV2 are placed in series and then connected to an ideal battery. V1 reads 80 V and has resistance 20KΩ and V2 has resistance 10KΩ . The EMF of the battery is:
240V
220V
160V
120V
To solve the problem, we need to find the EMF (Electromotive Force) of the battery when two voltmeters, V1 and V2, are connected in series.
1. Identify Given Values:
- Voltage reading of V1 ( V1=80V )
- Resistance of V1 ( R1=20kΩ=20,000Ω )
- Resistance of V2 ( R2=10kΩ=10,000Ω )
2. Calculate Total Resistance:
Since the voltmeters are connected in series, the total resistance Req is the sum of the individual resistances:
Req=R1+R2=20,000Ω+10,000Ω=30,000Ω
3. Use the Voltage Divider Rule:
The voltage across V1 can be expressed using the voltage divider rule:
V1=ϵReq⋅R1
Rearranging this gives:
ϵ=V1⋅ReqR1
4. Substitute Known Values:
Substitute V1=80V, Req=30,000Ω, and R1=20,000Ω:
ϵ=80V⋅30,000Ω20,000Ω
5. Simplify the Expression:
ϵ=80V⋅3020=80V⋅1.5=120V
6. Final Result:
Therefore, the EMF of the battery is:
ϵ=120V
Conclusion:
The EMF of the battery is 120V.
- Voltage reading of V1 ( V1=80V )
- Resistance of V1 ( R1=20kΩ=20,000Ω )
- Resistance of V2 ( R2=10kΩ=10,000Ω )
Since the voltmeters are connected in series, the total resistance Req is the sum of the individual resistances:
Req=R1+R2=20,000Ω+10,000Ω=30,000Ω
The voltage across V1 can be expressed using the voltage divider rule:
V1=ϵReq⋅R1
Rearranging this gives:
ϵ=V1⋅ReqR1
Substitute V1=80V, Req=30,000Ω, and R1=20,000Ω:
ϵ=80V⋅30,000Ω20,000Ω
ϵ=80V⋅3020=80V⋅1.5=120V
Therefore, the EMF of the battery is:
ϵ=120V
The EMF of the battery is 120V.
Topper's Solved these Questions
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-4
15 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET -5
15 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - LEVEL-1 DAILY TUTORIAL SHEET-2
15 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
Similar Questions
Voltmeters V1 and V2 are connected in series across a D.C. line V1 reads 80 volts and has a per volt resistance of 200ohms, V2 has a total resistance of 32 kilo ohms.
The line voltage is
View SolutionA battery of emf 2V and internal resistance 0.5(Ω)is connected across a resistance 1.5(Ω). Find the current flow through battery ?
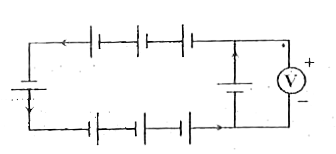
View Solutionin the circuit shown in the figure, each battery is of 5 V and has an internal resistance of 0.2 Omega What is the reading of the ideal voltmeter V
View SolutionAn ammeter and a voltmeter are connected in series to an ideal battery of emf E. If the ammeter reads I and voltmeter reading V, then
View SolutionA voltmeter of resistance 100Ω connected to the terminals of a cell reads 2 V. When the voltmeter is replaced by a resistance 1Ω and an ammeter of 1Ω , the ammeter reads 1 A. The EMF of the cell is __________ V.
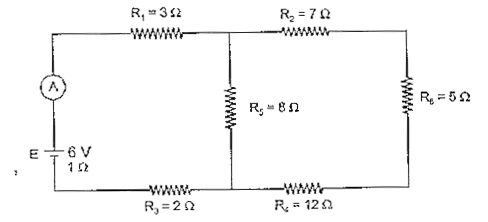
View SolutionIn the circuit shown below, E is a battery of emf 6 V and internal resistance 1Ω. Find the reading of the ammeter A. if it has negligible resistance :
View SolutionAn ideal voltmeter V is connected to a 2.0Ω resistor and a battery with emf 5.0V and internal resistance 0.5Ω as shown in figure
(a) What is the current in the 2.0Ω resistor?
(b) What is the terminal voltage of the battery?
(c) What is the reading of the voltmeter?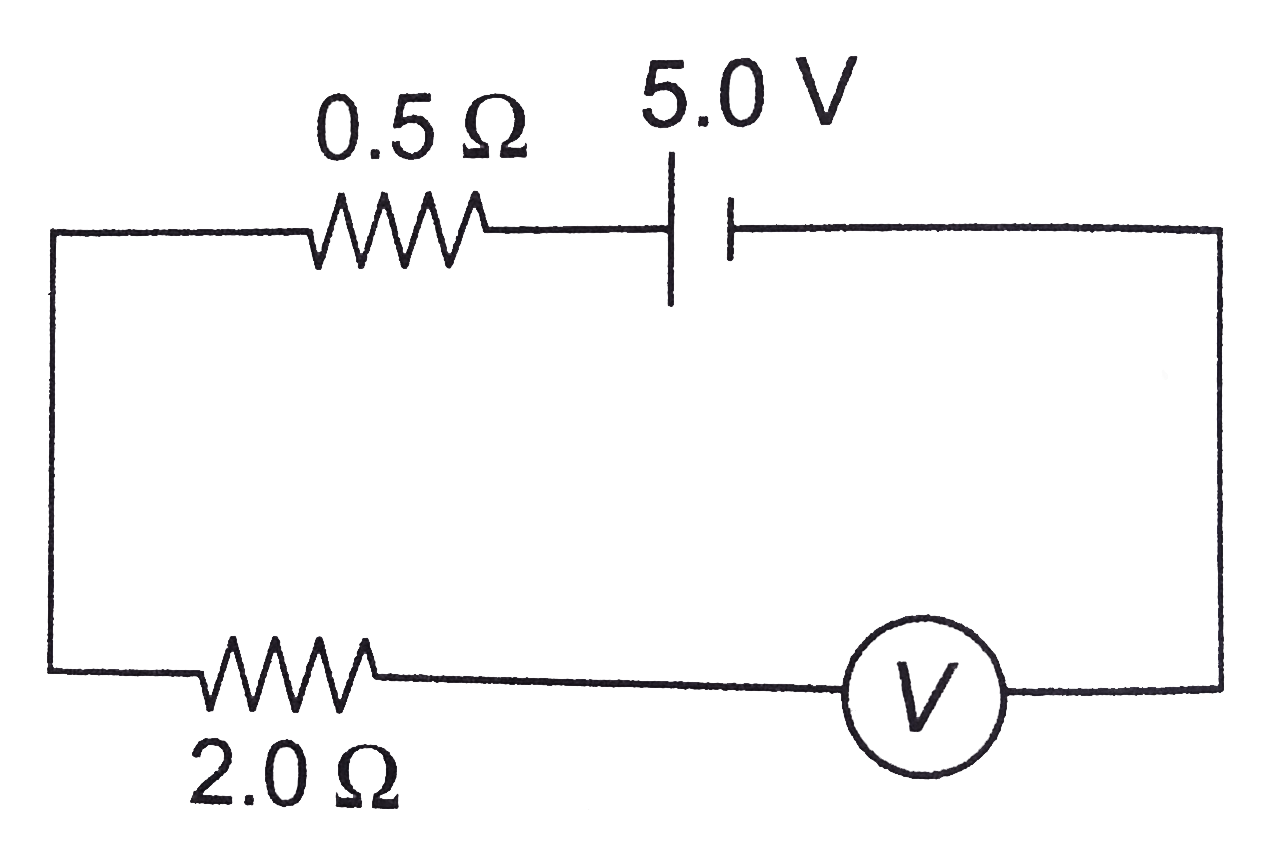
View SolutionA battery of EMF 10 V, with internal resistance 1Ω is being charged by a 120 V d.c. supply using a series resistance of 10Ω. The terminal voltage of the battery is
View SolutionA battery of emf 2 V and initial resistance 1Ω is
connected across terminals A and B of the circuit shown
in figure
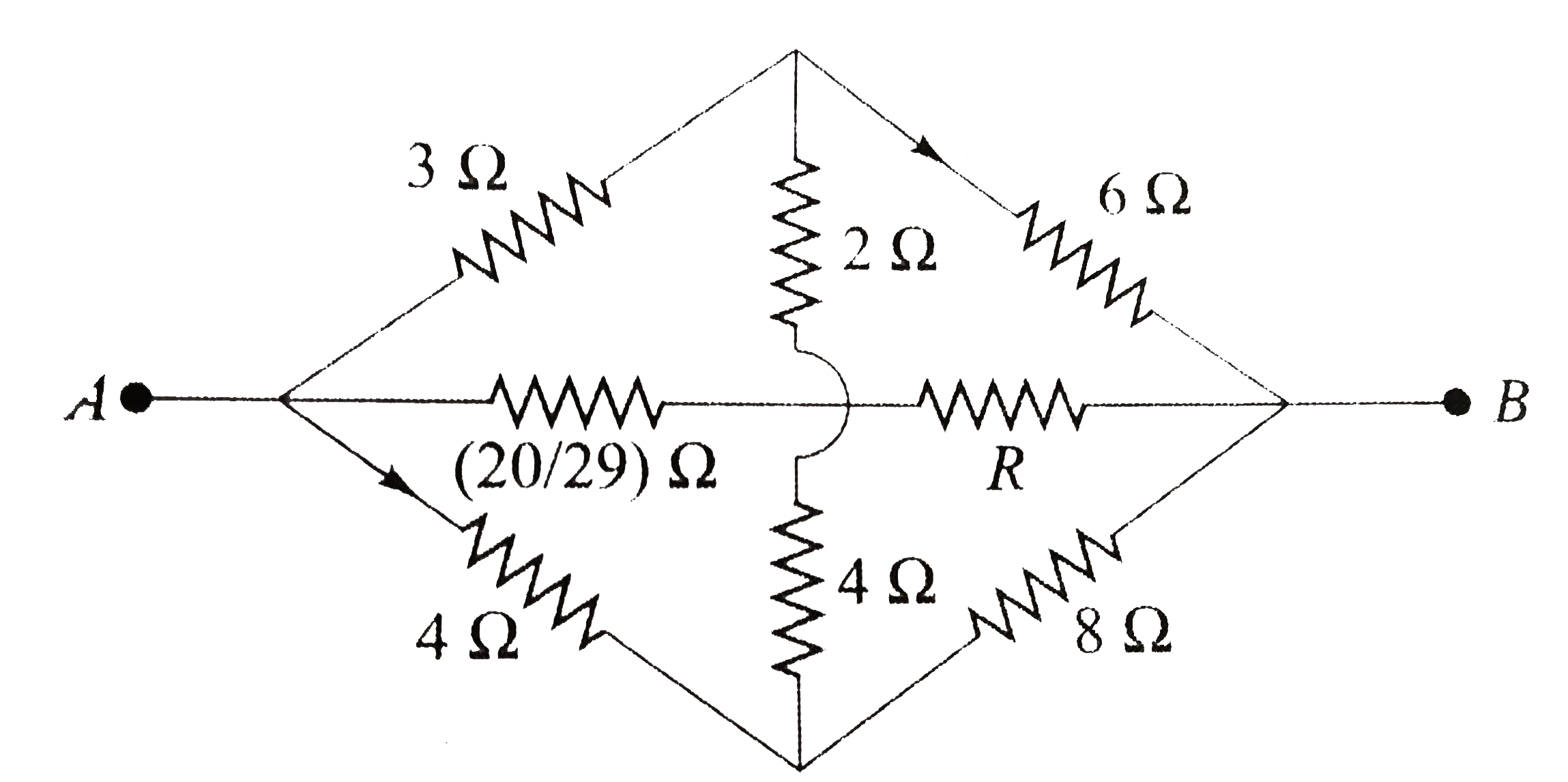 .
.
View SolutionA 10m long potentiometer wire has a resistance of 20 ohm. It is connected in series with a battery of emf 3V and a resistance of 10Ω. The internal resistance of cell is negligible. If he length can be read accurately up 10 1mm, the potentiometer can read voltage.
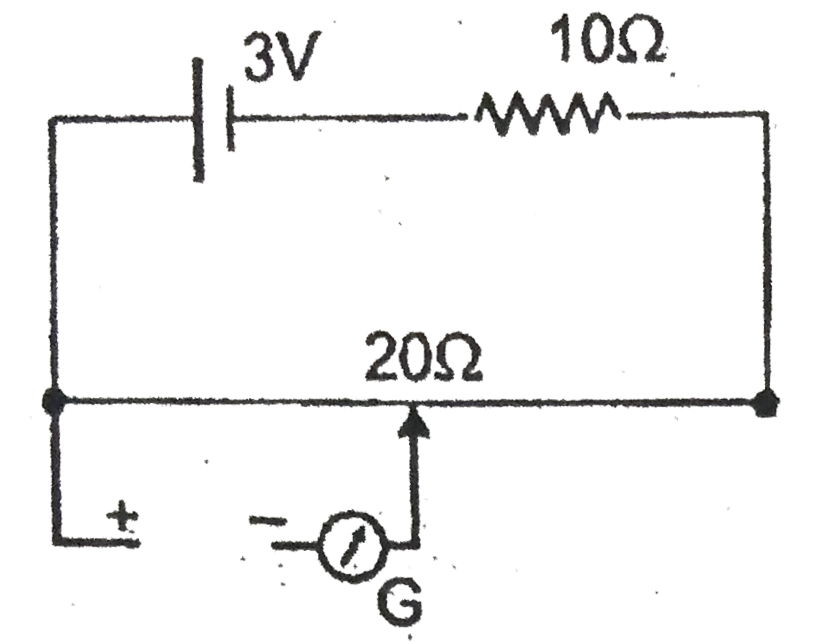
View Solution
