A voltmeter of resistance 100Ω connected to the terminals of a cell reads 2 V. When the voltmeter is replaced by a resistance 1Ω and an ammeter of 1Ω , the ammeter reads 1 A. The EMF of the cell is __________ V.
To solve the problem, we need to find the EMF (Electromotive Force) of the cell based on the information provided about the voltmeter and the ammeter setup. Let's break down the solution step by step.
Step 1: Understand the Setup with the Voltmeter
When the voltmeter (with resistance Rv=100Ω) is connected across the cell, it reads V=2V. The relationship between the EMF (E), the current (I), and the internal resistance (r) of the cell can be expressed as:
V=E−I⋅r
Here, the current I through the voltmeter can be calculated using Ohm's law:
I=ERv+r
Step 2: Write the Equation for the Voltmeter
Substituting I into the voltage equation gives:
2=E−(E100+r)⋅r
This simplifies to:
2=E−E⋅r100+r
Step 3: Understand the Setup with the Ammeter
When the voltmeter is replaced by a 1Ω resistor and a 1Ω ammeter, the total resistance in the circuit becomes R+1+1=r+2. The ammeter reads 1A, so we can write:
1=Er+2
From this, we can express E:
E=r+2
Step 4: Substitute and Solve
Now we have two equations:
1. 2=E−E⋅r100+r
2. E=r+2
Substituting E from the second equation into the first:
2=(r+2)−(r+2)⋅r100+r
Now, simplify this equation to find r:
2=r+2−(r+2)⋅r100+r
This leads to:
0=r−(r+2)⋅r100+r
Multiplying through by 100+r gives:
0=r(100+r)−(r+2)⋅r
This simplifies to:
0=100r
Thus, r=0.
Step 5: Find the EMF
Substituting r=0 back into the equation for E:
E=0+2=2V
Final Answer
The EMF of the cell is 2V.
---
When the voltmeter (with resistance Rv=100Ω) is connected across the cell, it reads V=2V. The relationship between the EMF (E), the current (I), and the internal resistance (r) of the cell can be expressed as:
V=E−I⋅r
Here, the current I through the voltmeter can be calculated using Ohm's law:
I=ERv+r
Substituting I into the voltage equation gives:
2=E−(E100+r)⋅r
This simplifies to:
2=E−E⋅r100+r
When the voltmeter is replaced by a 1Ω resistor and a 1Ω ammeter, the total resistance in the circuit becomes R+1+1=r+2. The ammeter reads 1A, so we can write:
1=Er+2
From this, we can express E:
E=r+2
Now we have two equations:
1. 2=E−E⋅r100+r
2. E=r+2
2=(r+2)−(r+2)⋅r100+r
Now, simplify this equation to find r:
2=r+2−(r+2)⋅r100+r
This leads to:
0=r−(r+2)⋅r100+r
Multiplying through by 100+r gives:
0=r(100+r)−(r+2)⋅r
This simplifies to:
0=100r
Thus, r=0.
Substituting r=0 back into the equation for E:
E=0+2=2V
The EMF of the cell is 2V.
Topper's Solved these Questions
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-1 JEE MAIN ARCHIVE
Explore 93 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:JEE ADVANCED ARCHIVE
Explore 68 Videos
- DC CIRCUITBook:VMC MODULES ENGLISHChapter:DC CIRCUITExercise:LEVEL-2 DAILY TUTORIAL SHEET-4
Explore 10 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
- DYNAMICS OF A PARTICLEBook:VMC MODULES ENGLISHChapter:DYNAMICS OF A PARTICLEExercise:JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
Explore 31 Videos
Similar Questions
Knowledge Check
The range of voltmeter of resistance 300Ω is 5 V. The resistance to be connected to convert it into an ammeter of range 5 A is
A1Ωin seriesB1Ωin parallelC0.1Ωin seriesD0.1Ωin parallel
A voltmeter with resistance 500Ω is used to measure the emf of a cell of internal resistance 4Ω. The percentage error in the reading of the voltmeter will be
View SolutionA cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω resistance, the ammeter reading is 0.04A. Find the voltage reading by the voltmeter and its resistance. Had the voltmeter been an ideal one what would have been its reading?
View SolutionA cell of emf 3.4V and internal resistance 3Ω is connected to an ammeter having resistance 2Ω and to an external resistance of 100Ω. When a voltmeter is connected across the 100Ω resistance, the ammeter reading is 0.04A. Find the voltage reading by the voltmeter and its resistance. Had the voltmeter been an ideal one what would have been its reading?
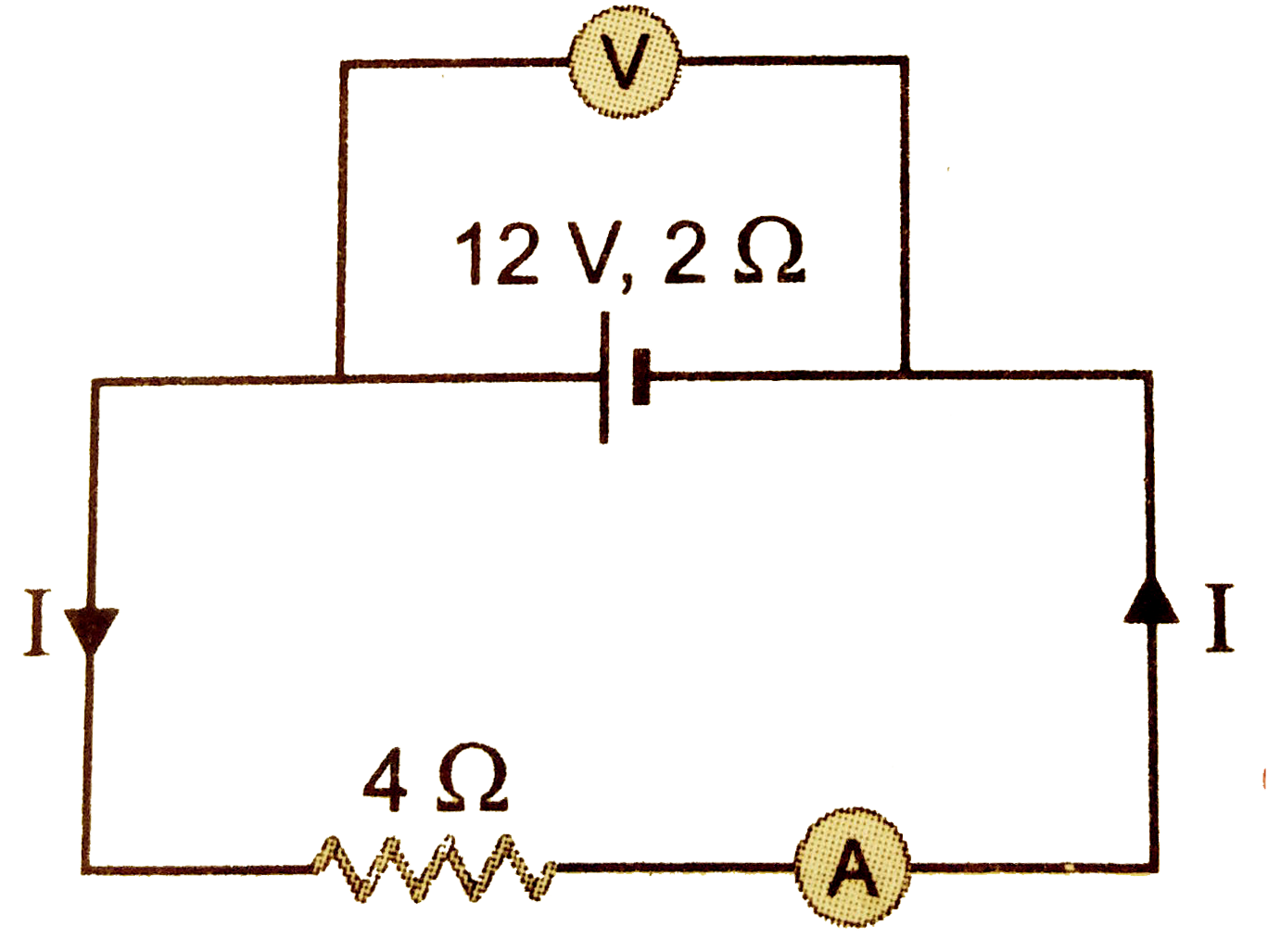
View SolutionA battery of emf 12V and internal resistance 2Ω is connected two a 4Ω resistor. Show that the a voltmeter when placed across cell and across the resistor in turn given the same reading
View SolutionWrite any two factors on which internal resistance of a cell depends . The reading on a high resistance voltmeter , when a cell is connected across it , is 2.0 V . When the terminals of the cell are also connected to a resistance of 3Ω as shown in the circuit , the voltmeter reading drops to 1.5 V . Find the internal resistance of the cell.
View SolutionGiven that the resistance the voltmeter is 200Ω. Find the voltmeter.s reading.
View SolutionFive identical lamps each of resistance R = 1500 Ω are connected to 300 V as shown in figure . The reading of ideal ammeter A is
View Solution
