Question

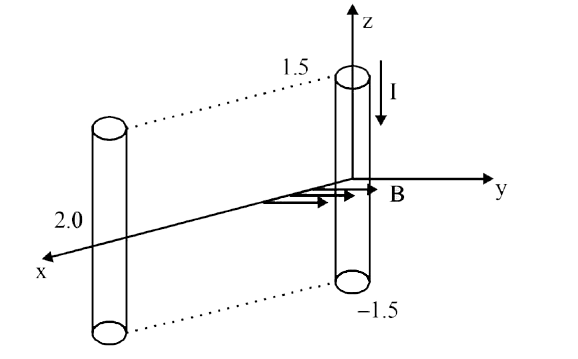
A conductor lies along the z-axis at $-1.5\le z\le 1.5$ m and carries a fixed current of $1.0A$ in $-{\hat{a}}_z$ direction (see figure). For a field $\overrightarrow{B}=3.0\times {10}^{-4}{e}^{-0.2x}{\hat{a}}_y$ T, find the power required to move the conductor at constant speed to $x=2.0m,y=m$ in $5\times {10}^{-3}s$. Assume parallel motion along the x-axis.

Options

A. 1.57 W
B. 2.97 W
C. 14.85 W
D. 29.7 W

Answer

B

Explanation

Force exerted on a current carrying conductor `F_("ext")=B(x)IL`
Averate power `=("Work done")/("Time taken") , P=1/t int_(0)^(2)F_("ext").dx=-1/tint_(0)^(2)B(x)ILdx`
`=1/(5xx10^(-3))int_(0)^(2)3xx10^(-04)e^(-0.2x)xx10xx3dx, =9[1-e^(-0.4)]=9[1-1/(e^(0.4))]=2.967~~2.97W`