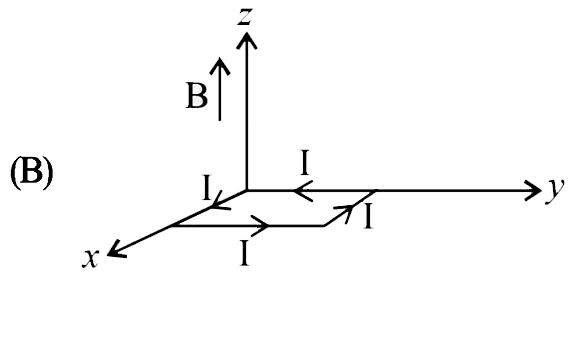
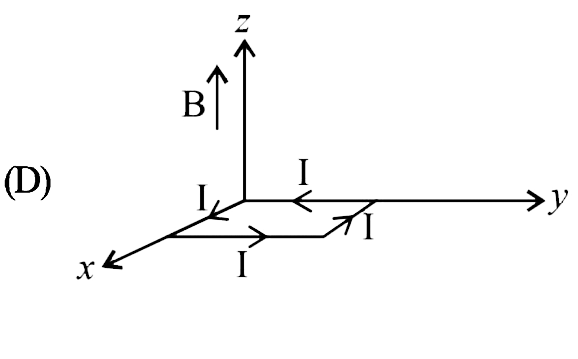
A uniform magnetic field B of 0.3 T is along the positive Z-direction. A rectangular loop (abcd) of sides 10 cm × 5 cm carries a current I of 12 A. Out of the following different orientations which one corresponds to stable equilibrium?




The correct Answer is:D
To determine which orientation of the rectangular loop corresponds to stable equilibrium in a uniform magnetic field, we can follow these steps:
Step 1: Understand the Concept of Magnetic Moment and Torque
The magnetic moment (m) of a current-carrying loop is given by:
m=I⋅A
where I is the current and A is the area vector of the loop. The torque (τ) experienced by the loop in a magnetic field (B) is given by:
τ=m×B
For stable equilibrium, the torque must be zero, which occurs when the angle θ between m and B is zero degrees (i.e., they are parallel).
Step 2: Analyze the Given Magnetic Field
The magnetic field B is given as 0.3T in the positive Z-direction. This means:
B=0.3^kT
Step 3: Determine the Magnetic Moment Direction for Each Orientation
1. Orientation A: Current flows anticlockwise when viewed from above.
- The area vector A will point in the positive X-direction.
- The angle θ between m (in X-direction) and B (in Z-direction) is 90∘.
- Not stable equilibrium (Torque is non-zero).
2. Orientation B: Current flows anticlockwise when viewed from below.
- The area vector A will point in the positive Z-direction.
- The angle θ between m (in Z-direction) and B (in Z-direction) is 0∘.
- Stable equilibrium (Torque is zero).
3. Orientation C: Current flows clockwise when viewed from above.
- The area vector A will point in the negative X-direction.
- The angle θ between m (in -X-direction) and B (in Z-direction) is 90∘.
- Not stable equilibrium (Torque is non-zero).
4. Orientation D: Current flows clockwise when viewed from below.
- The area vector A will point in the negative Z-direction.
- The angle θ between m (in -Z-direction) and B (in Z-direction) is 180∘.
- Not stable equilibrium (Torque is non-zero).
Conclusion
The only orientation that corresponds to stable equilibrium is Orientation B, where the magnetic moment is parallel to the magnetic field.
---
The magnetic moment (m) of a current-carrying loop is given by:
m=I⋅A
where I is the current and A is the area vector of the loop. The torque (τ) experienced by the loop in a magnetic field (B) is given by:
τ=m×B
For stable equilibrium, the torque must be zero, which occurs when the angle θ between m and B is zero degrees (i.e., they are parallel).
The magnetic field B is given as 0.3T in the positive Z-direction. This means:
B=0.3^kT
1. Orientation A: Current flows anticlockwise when viewed from above.
- The area vector A will point in the positive X-direction.
- The angle θ between m (in X-direction) and B (in Z-direction) is 90∘.
- Not stable equilibrium (Torque is non-zero).
- The area vector A will point in the positive Z-direction.
- The angle θ between m (in Z-direction) and B (in Z-direction) is 0∘.
- Stable equilibrium (Torque is zero).
- The area vector A will point in the negative X-direction.
- The angle θ between m (in -X-direction) and B (in Z-direction) is 90∘.
- Not stable equilibrium (Torque is non-zero).
- The area vector A will point in the negative Z-direction.
- The angle θ between m (in -Z-direction) and B (in Z-direction) is 180∘.
- Not stable equilibrium (Torque is non-zero).
The only orientation that corresponds to stable equilibrium is Orientation B, where the magnetic moment is parallel to the magnetic field.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 2
50 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
A uniform magnetic field of 3000G is established along the positive z-direction. A rectangular loop of sides 10cm and 5cm carries a current 12A. What is the torque on the loop in the different cases shown in the figure. What is the force on each case? Which case corresponds to stable equilibrium?

View SolutionFigure shows a square current carrying loop ABCD of side 10 cm and current i = 10A. The magnetic moment of the loop is:

View Solution
Knowledge Check
A uniform magnetic field of 1000 G is established along the positive z-direction. A rectangular loop of sides 10 cm and 5 cm carries a current of 12 A. What is the torque on the loop as shown in the figure?
 AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
AZeroB1.8×10−2NmC1.8×10−3NmD1.8×10−4Nm
A rectangular loop of dimensions (a×b) carries a current i. A uniform magnetic field →B=B0ˆi exists in space. Then :
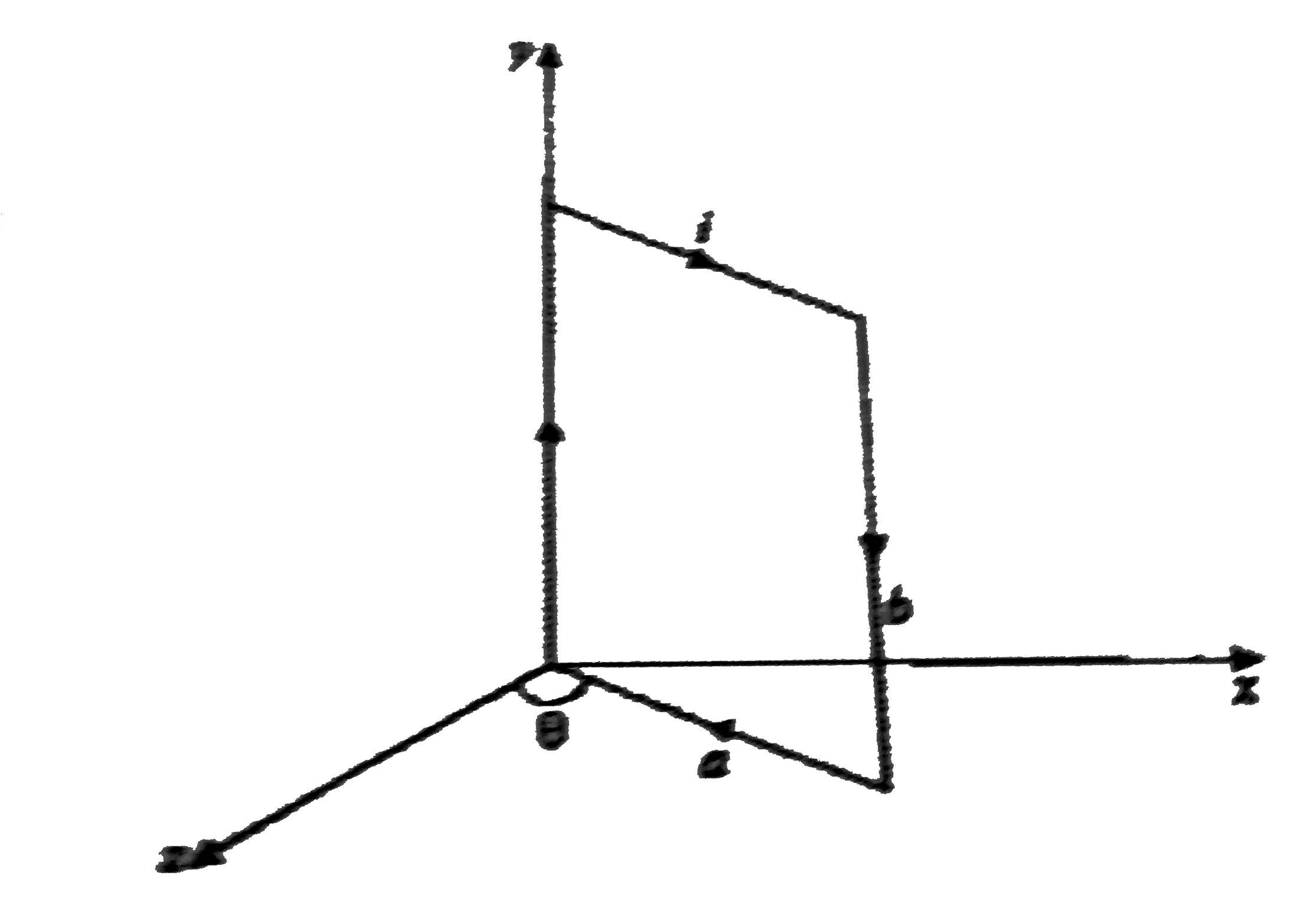
View SolutionA short bar magnet of moment 0⋅32JT−1 is placed in a uniform external magnetic field of 0⋅15T, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
View SolutionA short bar magnet of moment 0⋅32JT−1 is placed in a uniform external magnetic field of 0⋅15T, if the bar is free to rotate in the plane of the field, which orientations would correspond to its, (i) stable and (ii) unstable equilibrium? What is the potential energy of the magnet in each case?
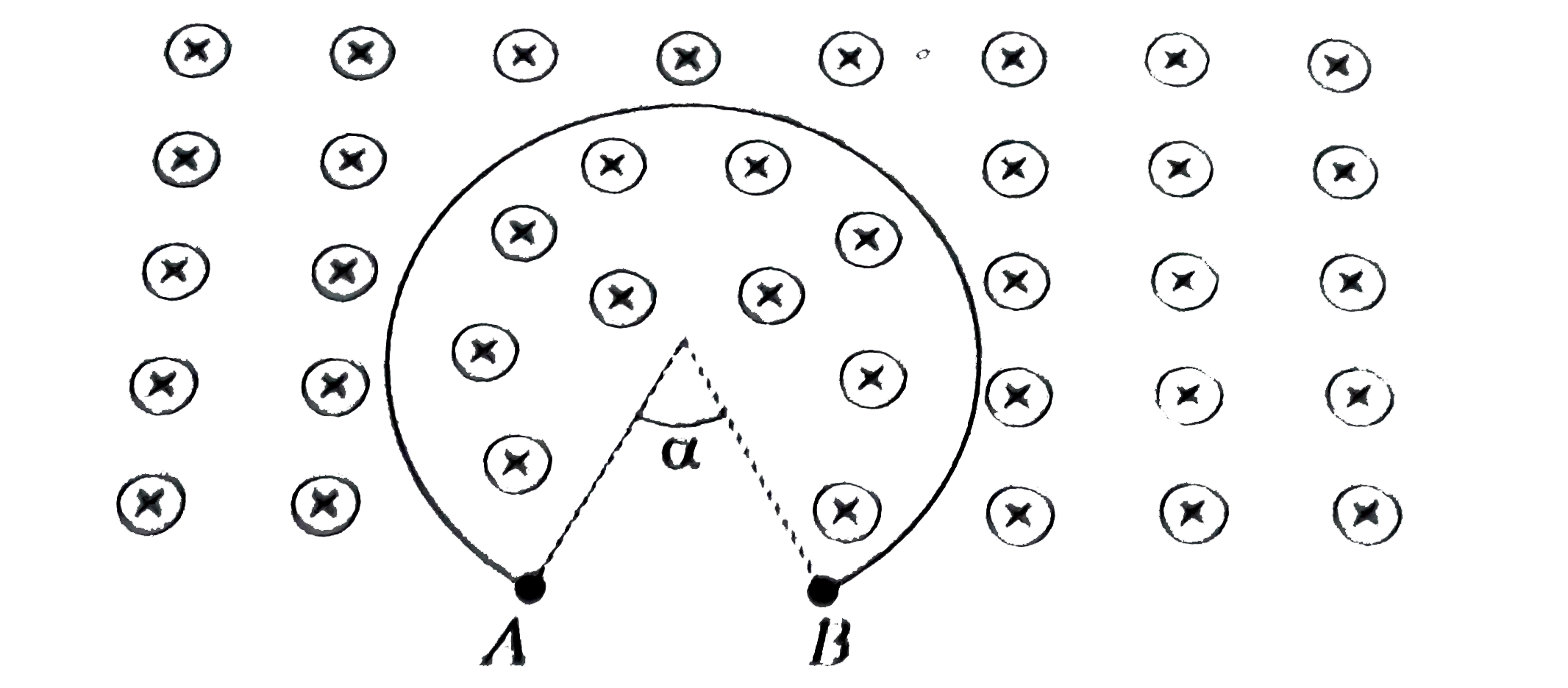
View SolutionA circular loop which is in the form of a major arc of a constant magnetic field B is applied in the vertical direction such that the magnetic lines of forces go into the plane. If R is the radius of circle and it carries a current I in the clockwise direction, then the force on the loop will be
View SolutionIf there is uniform magnetic field of in the positive z direction , in which orientations the loop would be in (i) stable equilibrium and (ii) unstable equilibrium ?


View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View SolutionA uniform magnetic field of 0.20×10−3T exists in the space. Find the the change in the magnetic scalar potential as one moves through 50cm along the field.
View Solution
