Find the magnitude of the magnetic fieldat the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
3μT
9μT
1μT
18μT
The correct Answer is:D
To find the magnitude of the magnetic field at the center of an equilateral triangular loop carrying a current, we can follow these steps:
1. Identify the Given Values:
- Side length of the triangle (a) = 1 m
- Current (I) = 10 A
- Permeability of free space (μ₀) = 4π×10−7NA−2
2. Determine the Distance from the Center to a Side (r):
- For an equilateral triangle, the distance from the center to a side (r) can be calculated using the formula:
r=a2√3
- Substituting the value of a:
r=12√3≈0.2887m
3. Use the Formula for Magnetic Field at the Center of an Equilateral Triangle:
- The formula for the magnetic field (B) at the center of an equilateral triangular loop is given by:
B=3μ0I4πr(sin60∘+sin60∘)
- Since sin60∘=√32, we can simplify:
B=3μ0I4πr(2⋅√32)=3μ0I√34πr
4. Substitute the Values into the Formula:
- Now substituting the values of μ₀, I, and r into the equation:
B=3×(4π×10−7)×10×√34π×(12√3)
5. Simplify the Expression:
- The 4π in the numerator and denominator cancels out:
B=3×10−7×10×√312√3
- This simplifies to:
B=3×10−7×10×2×3=18×10−6T
6. Convert to Microtesla:
- Since 1T=106μT:
B=18μT
Final Answer:
The magnitude of the magnetic field at the center of the equilateral triangular loop is 18 microtesla.
- Side length of the triangle (a) = 1 m
- Current (I) = 10 A
- Permeability of free space (μ₀) = 4π×10−7NA−2
- For an equilateral triangle, the distance from the center to a side (r) can be calculated using the formula:
r=a2√3
- Substituting the value of a:
r=12√3≈0.2887m
- The formula for the magnetic field (B) at the center of an equilateral triangular loop is given by:
B=3μ0I4πr(sin60∘+sin60∘)
- Since sin60∘=√32, we can simplify:
B=3μ0I4πr(2⋅√32)=3μ0I√34πr
- Now substituting the values of μ₀, I, and r into the equation:
B=3×(4π×10−7)×10×√34π×(12√3)
- The 4π in the numerator and denominator cancels out:
B=3×10−7×10×√312√3
- This simplifies to:
B=3×10−7×10×2×3=18×10−6T
- Since 1T=106μT:
B=18μT
The magnitude of the magnetic field at the center of the equilateral triangular loop is 18 microtesla.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:JEE Advanced (Archive)
Explore 78 Videos
- MAGNETIC EFFECTS OF CURRENT Book:VMC MODULES ENGLISHChapter:MAGNETIC EFFECTS OF CURRENT Exercise:LEVEL 2
Explore 50 Videos
- LIQUIDSBook:VMC MODULES ENGLISHChapter:LIQUIDSExercise:JEE ADVANCED (LEVEL -2)
Explore 55 Videos
- MOCK TEST 1Book:VMC MODULES ENGLISHChapter:MOCK TEST 1Exercise:PART I : PHYSICS (SECTION-2)
Explore 10 Videos
Similar Questions
Find the magnitude of the magnetic field at the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
View SolutionThe magnitude of the magnetic field at the center of an equilateral triangular loop of side 1 m which is carrying a current of 10 A (in μT) is ___________ .
[Take μ0=4π×10−7NA−2]
View SolutionThe magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionFind the magnetic field at point P due to a straight line segment AB of length 6cm carrying a current of 5A. (See figure)
(μ0=4π×10−7N−A−2).
 .
.
View SolutionA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)
View SolutionMagnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side 10cm , 50 turns and carrying current I (Ampere) in units of μ0Iπ is :
View SolutionTwo charges of 4μC each are placed at the corners A and B of an equilaternal triangle of side length 0.2m in air. The
electric potential at C is [14πε0=9×109N−m2C2]
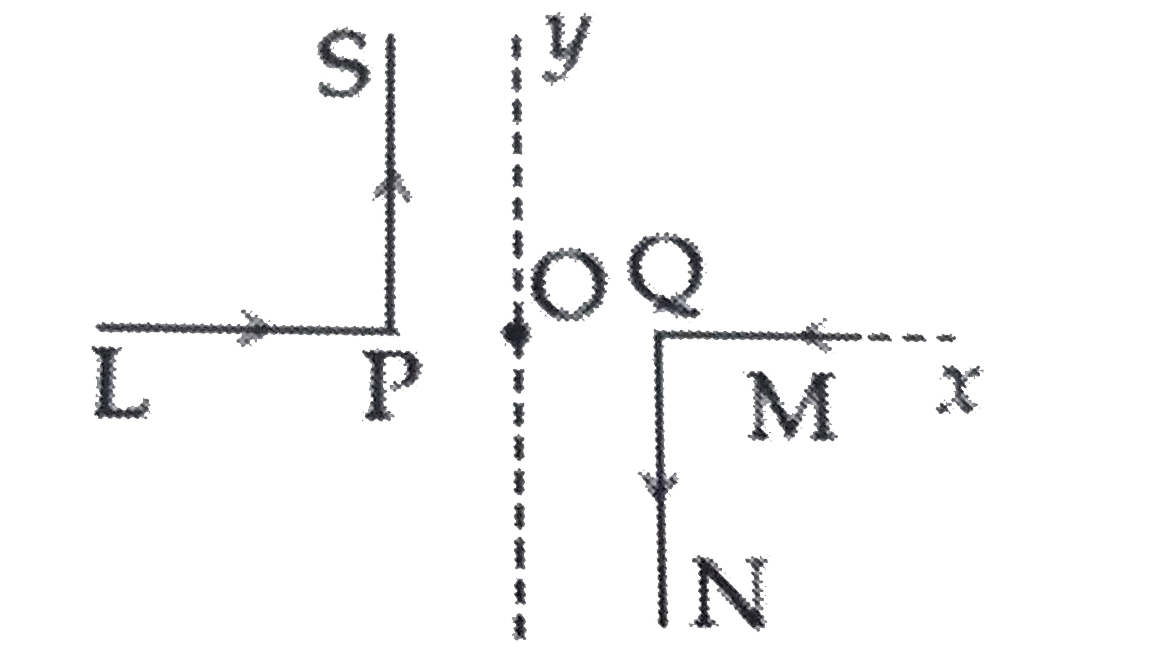
View SolutionAs shown in the figure two infinitely long, identical wires are bent by 90∘ and placed in such a way that the segments LP and QM are along the x-axis , while segments PS and QN are parallel to the Y-axis If OP=OQ=4 cm ,and the magnitude of the magnetic field at O is 10−4 T, and the magnitude of the current in each wire and the direction of the magnetic field at O will be
(μo=4π×10−7NA−2):
View SolutionFind the magnitude of magetic moment of the current carrying lop ABCDEFA. Each side of the loop is 10cm long and current in the loop is i=2.0A
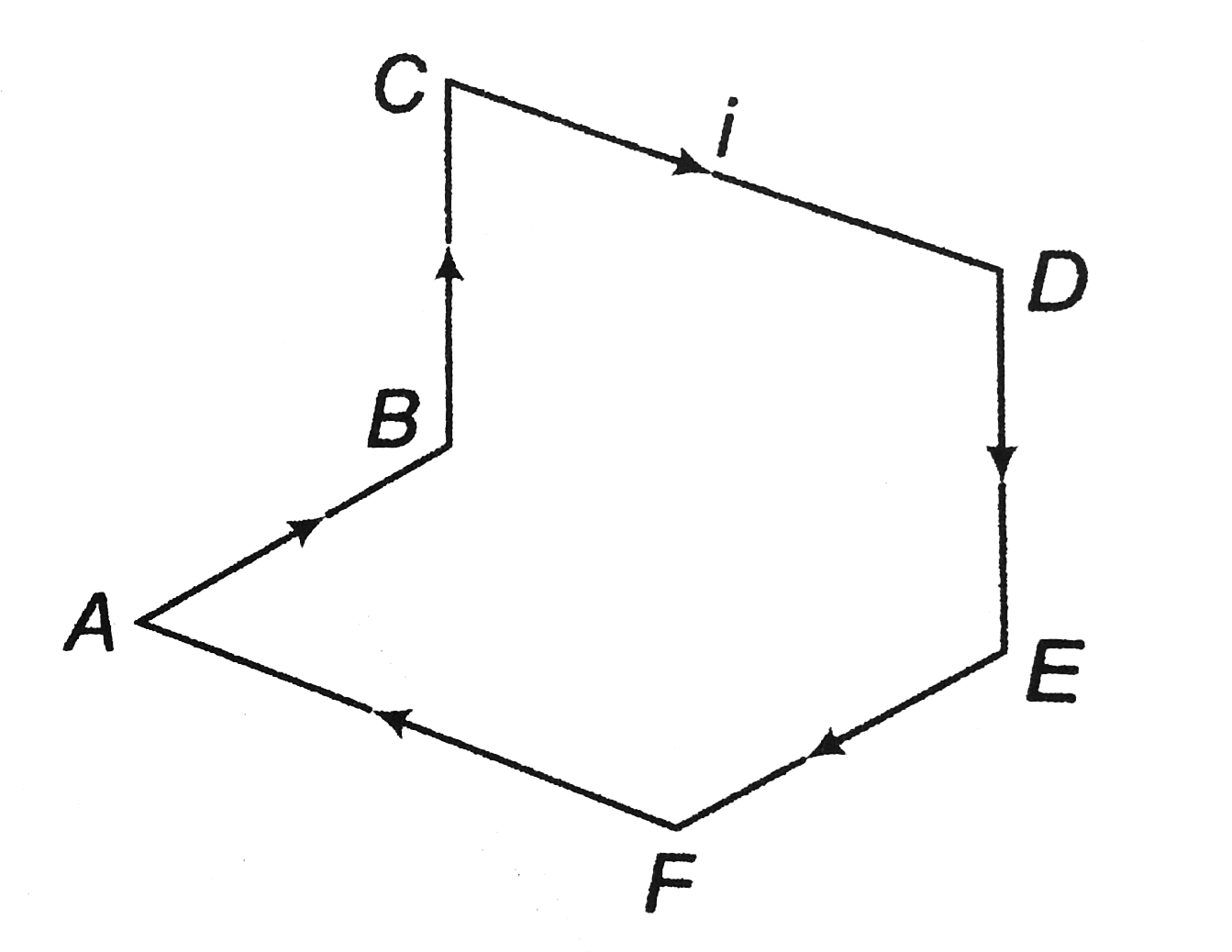
View SolutionFind the magnitude of magetic moment of the current carrying lop ABCDEFA. Each side of the loop is 10cm long and current in the loop is i=2.0A

View Solution
