The magnitude of the magnetic field at the center of an equilateral triangular loop of side 1 m which is carrying a current of 10 A (in μT) is ___________ .
[Take μ0=4π×10−7NA−2]
The correct Answer is:18
To find the magnitude of the magnetic field at the center of an equilateral triangular loop of side 1 m carrying a current of 10 A, we can follow these steps:
Step 1: Understand the Geometry
We have an equilateral triangle with each side A=1m. The center of the triangle is known as the centroid.
Step 2: Determine the Distance from the Centroid to a Vertex
The distance r from the centroid to any vertex of the triangle can be calculated using the formula:
r=A√3
Substituting A=1m:
r=1√3≈0.577m
Step 3: Calculate the Magnetic Field Contribution from One Side
The magnetic field B at the center due to a straight current-carrying wire is given by:
B=μ0I4πrsinθ
For an equilateral triangle, the angle θ between the line from the center to the vertex and the perpendicular from the center to the wire is 60∘. Thus, sin60∘=√32.
Step 4: Substitute Values into the Formula
Using μ0=4π×10−7N/A2 and I=10A:
B=(4π×10−7)×104π×1√3⋅√32
This simplifies to:
B=10×10−71√3⋅√32
B=10×10−7⋅12=5×10−7T
Step 5: Total Magnetic Field from All Three Sides
Since there are three sides contributing equally to the magnetic field:
Btotal=3B=3×5×10−7T=15×10−7T
To convert this to microtesla (μT):
Btotal=15×10−1μT=15μT
Final Answer
The magnitude of the magnetic field at the center of the equilateral triangular loop is:
15μT
We have an equilateral triangle with each side A=1m. The center of the triangle is known as the centroid.
The distance r from the centroid to any vertex of the triangle can be calculated using the formula:
r=A√3
Substituting A=1m:
r=1√3≈0.577m
The magnetic field B at the center due to a straight current-carrying wire is given by:
B=μ0I4πrsinθ
For an equilateral triangle, the angle θ between the line from the center to the vertex and the perpendicular from the center to the wire is 60∘. Thus, sin60∘=√32.
Using μ0=4π×10−7N/A2 and I=10A:
B=(4π×10−7)×104π×1√3⋅√32
This simplifies to:
B=10×10−71√3⋅√32
B=10×10−7⋅12=5×10−7T
Since there are three sides contributing equally to the magnetic field:
Btotal=3B=3×5×10−7T=15×10−7T
To convert this to microtesla (μT):
Btotal=15×10−1μT=15μT
The magnitude of the magnetic field at the center of the equilateral triangular loop is:
15μT
Topper's Solved these Questions
- JEE MAIN REVISION TEST - 13Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 13Exercise:PHYSICS (SECTION 2)
Explore 5 Videos
- JEE MAIN REVISION TEST - 12 Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 12 Exercise:PHYSICS
Explore 25 Videos
- JEE MAIN REVISION TEST - 18Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISION TEST - 18Exercise:PHYSICS - SECTION 2
Explore 5 Videos
Similar Questions
The magnetic field at the centre of an equilateral triangular loop of side 2L and carrying a current i is
View SolutionFind the magnitude of the magnetic field at the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
View SolutionFind the magnitude of the magnetic fieldat the center of an equilateral triangular loop of side length 1m which is carrying a current of 10A. ( Take μ0=4π×10−7NA−2)
View SolutionA long straight wire is carrying a current of 12 A . The magnetic field at a distance of 8 cm is
(μ0=4π×10−7NA2)
View SolutionMagnitude of magnetic field (in SI units) at the centre of a hexagonal shape coil of side 10cm , 50 turns and carrying current I (Ampere) in units of μ0Iπ is :
View SolutionFind net force on the equilateral loop of side m carrying a current of 2A kept in a uniform magnetic field of 2T as shown in figure.
View SolutionFind the magnetic field at point P due to a straight line segment AB of length 6cm carrying a current of 5A. (See figure)
(μ0=4π×10−7N−A−2).
 .
.
View SolutionFind the magnitude of magetic moment of the current carrying lop ABCDEFA. Each side of the loop is 10cm long and current in the loop is i=2.0A
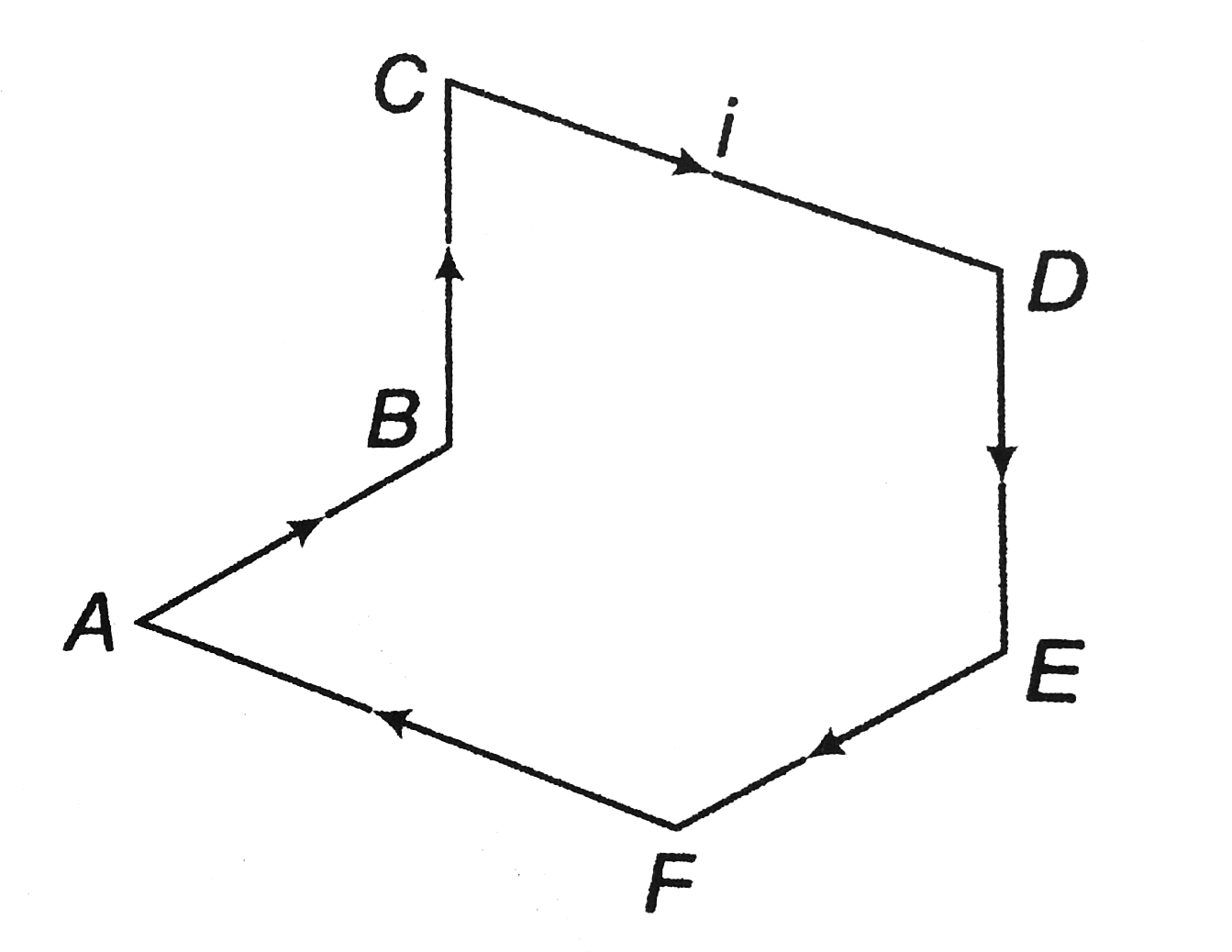
View SolutionFind the magnitude of magetic moment of the current carrying lop ABCDEFA. Each side of the loop is 10cm long and current in the loop is i=2.0A

View SolutionThree particles, each having a charge of 10μC are placed at the coners of an equilateral triangle of side 10cm. The electrostatic potential energy of the system is (Given 14πε0=9×109N−m2/C2)
View Solution

