Two very long straight parallel wires, parallel to y-axis, carry currents 41 and I, along+y direction and-y direaction respectively. The wires are passes through the x-axis at the points (d,0,0) and (−d,0,0) respectively. The graph of magnetic field z-component as one moves along the x-axis from x=−d to x=+d, is best given by




The correct Answer is:C
To solve the problem regarding the magnetic field due to two long straight parallel wires, we can follow these steps:
Step 1: Understand the Configuration
We have two long straight parallel wires:
- Wire 1 carries a current of 4I in the +y direction and is located at the point (d,0,0).
- Wire 2 carries a current of I in the -y direction and is located at the point (−d,0,0).
Step 2: Determine the Magnetic Field Contributions
Using the right-hand rule and the Biot-Savart law, we can find the direction of the magnetic field produced by each wire at a point along the x-axis.
1. Magnetic Field due to Wire 1 (at x=d):
- The magnetic field B1 at a point x (where x>d) due to Wire 1 is directed out of the page (in the +z direction).
- The magnitude of the magnetic field is given by:
B1=μ0(4I)2πr1
where r1=x−d.
2. Magnetic Field due to Wire 2 (at x=−d):
- The magnetic field B2 at a point x (where x<−d) due to Wire 2 is also directed out of the page (in the +z direction).
- The magnitude of the magnetic field is given by:
B2=μ0I2πr2
where r2=x+d.
Step 3: Combine the Magnetic Fields
For x between −d and d:
- The magnetic field contributions from both wires will add up since they are in the same direction (both in the +z direction).
- The total magnetic field B at a point x is:
B=B1+B2=μ0(4I)2π(d−x)+μ0I2π(d+x)
Step 4: Analyze the Behavior of the Magnetic Field
- As x approaches −d, B2 becomes very large (approaches infinity) because r2 approaches zero.
- As x approaches d, B1 becomes very large (also approaches infinity).
- There will be a point between −d and d where the magnetic field is at a minimum due to the opposing effects of the two currents.
Step 5: Find the Minimum Magnetic Field
To find the point where the magnetic field is minimum, we can differentiate B with respect to x and set it to zero:
dBdx=0
This will give us the position where the magnetic field is minimized.
Step 6: Solve for the Minimum Point
After differentiating and simplifying, we find that the magnetic field is minimized at:
x=2d3
This point is closer to Wire 2 than to Wire 1, indicating that the magnetic field strength will be lower there.
Step 7: Graph the Magnetic Field
The graph of the magnetic field B as a function of x will show:
- Very high values (approaching infinity) at x=−d and x=d.
- A minimum value at x=2d3.
Conclusion
The best representation of the magnetic field's z-component as one moves along the x-axis from x=−d to x=d is a graph that shows the magnetic field increasing to infinity at both ends and having a minimum at x=2d3.
We have two long straight parallel wires:
- Wire 1 carries a current of 4I in the +y direction and is located at the point (d,0,0).
- Wire 2 carries a current of I in the -y direction and is located at the point (−d,0,0).
Using the right-hand rule and the Biot-Savart law, we can find the direction of the magnetic field produced by each wire at a point along the x-axis.
- The magnetic field B1 at a point x (where x>d) due to Wire 1 is directed out of the page (in the +z direction).
- The magnitude of the magnetic field is given by:
B1=μ0(4I)2πr1
where r1=x−d.
- The magnetic field B2 at a point x (where x<−d) due to Wire 2 is also directed out of the page (in the +z direction).
- The magnitude of the magnetic field is given by:
B2=μ0I2πr2
where r2=x+d.
For x between −d and d:
- The magnetic field contributions from both wires will add up since they are in the same direction (both in the +z direction).
- The total magnetic field B at a point x is:
B=B1+B2=μ0(4I)2π(d−x)+μ0I2π(d+x)
- As x approaches −d, B2 becomes very large (approaches infinity) because r2 approaches zero.
- As x approaches d, B1 becomes very large (also approaches infinity).
- There will be a point between −d and d where the magnetic field is at a minimum due to the opposing effects of the two currents.
To find the point where the magnetic field is minimum, we can differentiate B with respect to x and set it to zero:
dBdx=0
This will give us the position where the magnetic field is minimized.
After differentiating and simplifying, we find that the magnetic field is minimized at:
x=2d3
This point is closer to Wire 2 than to Wire 1, indicating that the magnetic field strength will be lower there.
The graph of the magnetic field B as a function of x will show:
- Very high values (approaching infinity) at x=−d and x=d.
- A minimum value at x=2d3.
The best representation of the magnetic field's z-component as one moves along the x-axis from x=−d to x=d is a graph that shows the magnetic field increasing to infinity at both ends and having a minimum at x=2d3.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Main (Archive)
75 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 1
75 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
Two long parallel wires, AB and CD, carry equal currents in opposite directions. They lie in the x-y plane, parallel to the x-axis, and pass through the points (0,-a,0) and (0,a,0) respectively, Figure. The resultant magnetic field is:
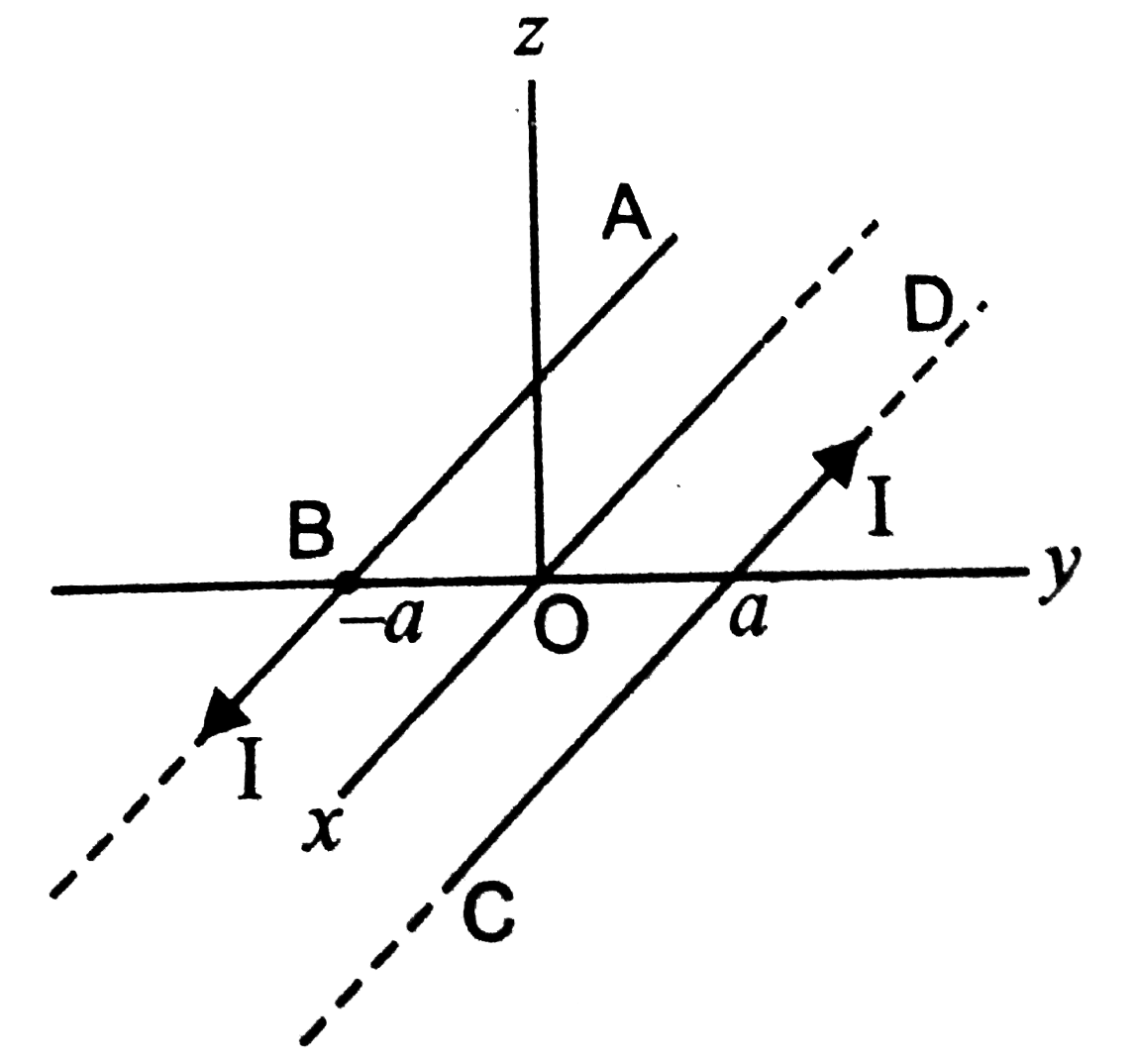
View SolutionTwo long wires are kept along x and y axis they carry currents I&II respectively in +ve× and +vey direction respectively.Find →B at point (0,0,d)
View SolutionTwo long straight currents carrying wires having currents I and 2I lie along y-and z-axis, respectively, as shown in Fig. Find →B at a point P(x,0).

View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionFour points charges -q,+q,+q and -q are placed on y-axis at y=-2d, y=-d,y=+d and y=+2d, respectively. The magnitude of the electric field E at a point on the x-axis at x=D, with D>>d, will behave as :
View SolutionTwo point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionThe location of three long wires carrying same current I are x=−a, x=0 and x=+ a respectively as shown in figure. The magnetic field at point (0, 0, a) is
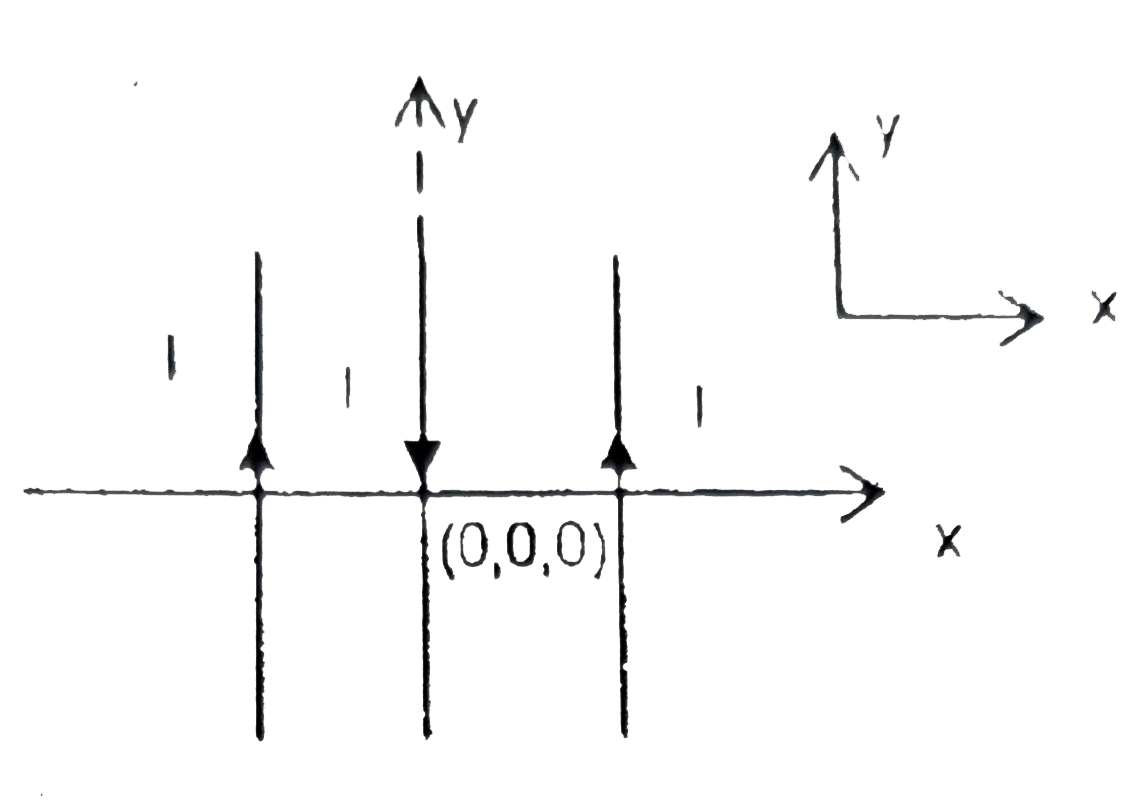
View SolutionTwo infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View Solution
