Two long wires are kept along x and y axis they carry currents I&II respectively in +ve× and +vey direction respectively.Find →B at point (0,0,d)
The correct Answer is:μ0i2πd(ˆi−ˆj)
To find the magnetic field →B at the point (0,0,d) due to two long wires carrying currents along the x-axis and y-axis, we can follow these steps:
Step 1: Understand the Setup
We have two long straight wires:
- Wire 1 is along the x-axis and carries current I in the positive x-direction.
- Wire 2 is along the y-axis and carries current II in the positive y-direction.
We need to find the magnetic field at the point (0,0,d).
Step 2: Use the Biot-Savart Law
The magnetic field →B due to a long straight wire carrying current I at a distance r from the wire is given by the formula:
→B=μ0I2πr^n
where μ0 is the permeability of free space, and ^n is the unit vector in the direction given by the right-hand rule.
Step 3: Calculate the Magnetic Field from Wire 1
For Wire 1 (along the x-axis):
- The distance from the wire to the point (0,0,d) is r=0 (along the y-axis).
- The magnetic field →B1 at point (0,0,d) will be directed in the negative z-direction (using the right-hand rule).
Thus, the magnetic field due to Wire 1 is:
→B1=μ0I2πd(−^j)
Step 4: Calculate the Magnetic Field from Wire 2
For Wire 2 (along the y-axis):
- The distance from the wire to the point (0,0,d) is also r=0 (along the x-axis).
- The magnetic field →B2 at point (0,0,d) will be directed in the negative z-direction as well.
Thus, the magnetic field due to Wire 2 is:
→B2=μ0II2πd(−^i)
Step 5: Combine the Magnetic Fields
The total magnetic field →B at point (0,0,d) is the vector sum of →B1 and →B2:
→B=→B1+→B2
Substituting the values:
→B=μ0I2πd(−^j)+μ0II2πd(−^i)
→B=−μ0I2πd^j−μ0II2πd^i
Final Result
Thus, the magnetic field →B at point (0,0,d) is:
→B=−μ0I2πd^i−μ0II2πd^j
We have two long straight wires:
- Wire 1 is along the x-axis and carries current I in the positive x-direction.
- Wire 2 is along the y-axis and carries current II in the positive y-direction.
The magnetic field →B due to a long straight wire carrying current I at a distance r from the wire is given by the formula:
→B=μ0I2πr^n
where μ0 is the permeability of free space, and ^n is the unit vector in the direction given by the right-hand rule.
For Wire 1 (along the x-axis):
- The distance from the wire to the point (0,0,d) is r=0 (along the y-axis).
- The magnetic field →B1 at point (0,0,d) will be directed in the negative z-direction (using the right-hand rule).
→B1=μ0I2πd(−^j)
For Wire 2 (along the y-axis):
- The distance from the wire to the point (0,0,d) is also r=0 (along the x-axis).
- The magnetic field →B2 at point (0,0,d) will be directed in the negative z-direction as well.
→B2=μ0II2πd(−^i)
The total magnetic field →B at point (0,0,d) is the vector sum of →B1 and →B2:
→B=→B1+→B2
Substituting the values:
→B=μ0I2πd(−^j)+μ0II2πd(−^i)
→B=−μ0I2πd^j−μ0II2πd^i
Thus, the magnetic field →B at point (0,0,d) is:
→B=−μ0I2πd^i−μ0II2πd^j
Topper's Solved these Questions
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-183videos
ELECTRODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Exercise-1 PART-254videos
ELECTRODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems31videos
ELECTRODYNAMICS
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTRO MAGNETIC WAVESEXERCISE - Exercise 327videos
ELECTRO MAGNETIC WAVES
- BOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P19videos
ELECTROMAGNETIC INDUCTION
Similar Questions
Two infinitely long, thin, insulated, straight wires lie in the x-y plane along the x- and y- axis respectively. Each wire carries a current I, respectively in the positive x-direction and positive y-direction. The magnetic field will be zero at all points on the straight line:
View SolutionTwo very long straight parallel wires, parallel to y-axis, carry currents 41 and I, along+y direction and-y direaction respectively. The wires are passes through the x-axis at the points (d,0,0) and (−d,0,0) respectively. The graph of magnetic field z-component as one moves along the x-axis from x=−d to x=+d, is best given by
View SolutionIn the figure, OA and OB are two uniformly charged wires, placed along x and y axis respectively. Find the unit vector in the direction of field at point (0,0,√3L).
 View Solution
View SolutionTwo long straight currents carrying wires having currents I and 2I lie along y-and z-axis, respectively, as shown in Fig. Find →B at a point P(x,0).
 View Solution
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire along the z- axis carries a current I in the negative z−direction . The magnetic vector field →B at a point having coordinates (x,y) in the Z=0 plane is
View SolutionA long straight wire is kept along x-axis. It carries a current i in the positive x-direction. A proton and an electron are placed at (0, a,0) and (0, -a, 0) respecitively. The proton is imparted an initial velocity v along +z axis and the electron is imparted an initial velocity v along +x-axis. The magnetic forces experienced by the two particles at the instant are
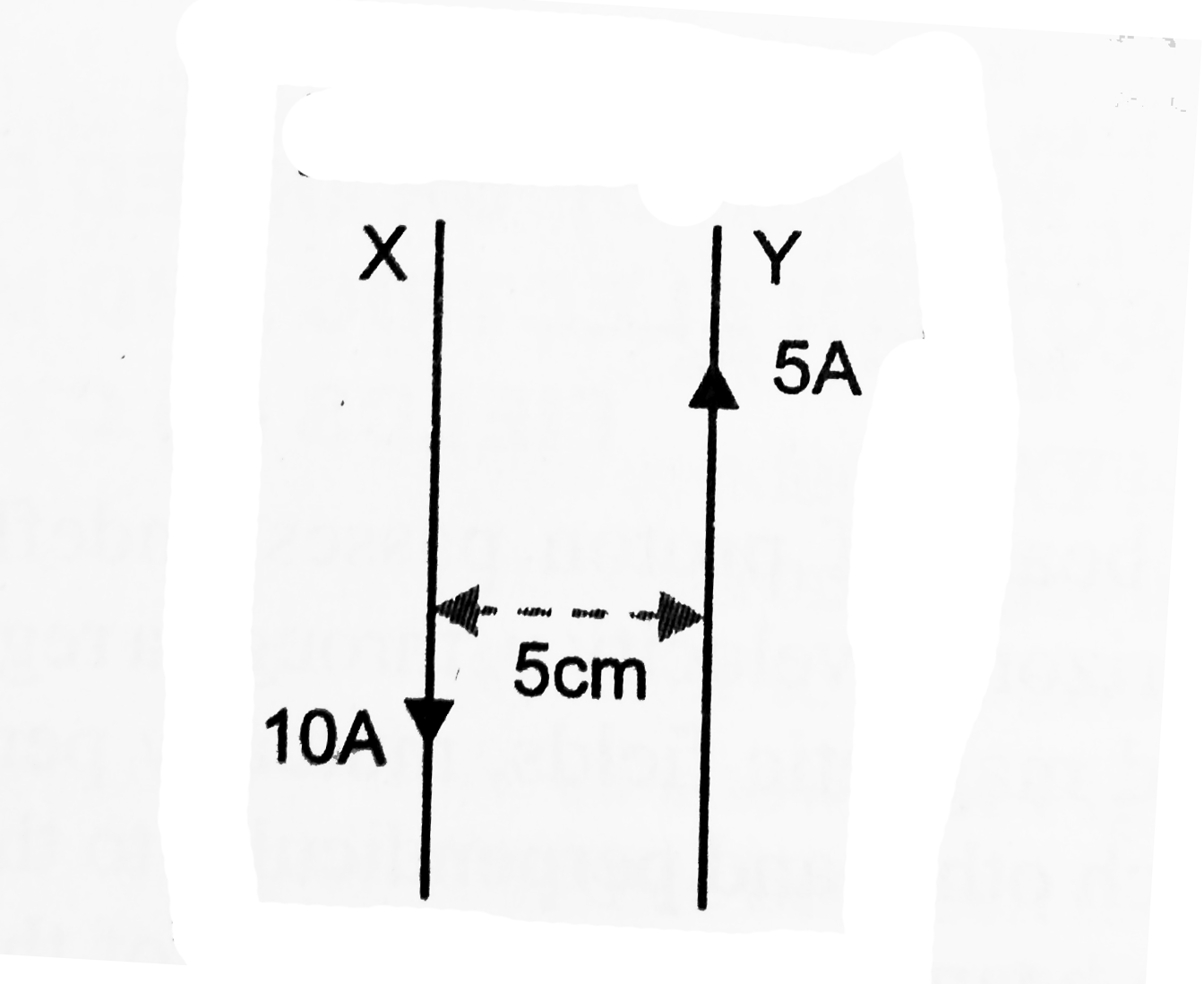
View SolutionTwo long parallel straight wires X and Y separated by a distance 5cm in air carry currents of 10A and 5A respectively in opposite directions. Calculate the magnitude and direction of force on a 20cm length of the wire Y. Figure
 View Solution
View SolutionTwo long, straight wires, each carrying a current of 5A, are placed along the x and y axes respectively. The currents point along the positive directions of the axes. Find the magnetic fields at the points (a) (1m, 1m), (b) (-1m, 1m), (c) (-1m, -1m) and (d) (1m, -1m).
View SolutionOne long conductor carries current I along y-axis with charge density λ. An electric field exists along z-axis. In what direction, a charged particle at point P, distance x apart from the wire (along x-axis), be projected with velocity v so that it moves undeflected?
 View Solution
View Solution
