A loop in the shape of an equilateral triangle triangle of side a carries a current I as shown in the figure.Find out the magnetic field at the centre C of the triangle.

Video Solution
Text Solution
The correct Answer is:9μ0i2πa
B=B1+B2+B3=3B1
=3μ04π×i(a2√3)×(sin60∘+sin60∘)=9μ0i2πa
|
Topper's Solved these Questions
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Exercise-1 PART-1
Explore 83 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Exercise-1 PART-2
Explore 54 Videos
- ELECTRODYNAMICSBook:RESONANCE ENGLISHChapter:ELECTRODYNAMICSExercise:Advanced level problems
Explore 31 Videos
- ELECTRO MAGNETIC WAVESBook:RESONANCE ENGLISHChapter:ELECTRO MAGNETIC WAVESExercise:Exercise 3
Explore 27 Videos
- ELECTROMAGNETIC INDUCTIONBook:RESONANCE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:A.l.P
Explore 19 Videos
Similar Questions
Knowledge Check
Find the area of an equilateral triangle with a side length of 12
A6√3B18√3C36√3D72√3
Find the area of an equilateral triangle having each side x cm
View SolutionFind the perimeter of an equilateral triangle of side 13 cm.
View SolutionFind the area of an equilateral triangle having each side 4cm.
View SolutionFind the perimeter of an equilateral triangle with side 9cm.
View SolutionThe wire loop shown in figure carries a current as shown. The magnetic field at the centre O is ,
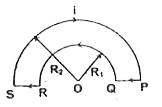
View SolutionIf the side of an equilateral triangle is doubled, find the new perimeter.
View SolutionA conducting circular loop of radius a is connected to two long, straight wires . The straight wires carry a current I as shown in figure . Find the magnetic field B at the centre of the loop.

View Solution

