Two point charges (Q each are placed at (0,y) and (0-y) A point charge q of the same polarity can move along the x-axis. Then
the force on q is maximum at x=±y/√2
the charge q is in equilibrium at the origin
the charge q performs an oscillatory motion about the origin
for any position of q other than origin the force is directed away from origin
The correct Answer is:A, B, D
To solve the problem, we need to analyze the forces acting on a point charge q that can move along the x-axis due to the presence of two other point charges Q placed at coordinates (0, y) and (0, -y). Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Setup
We have two point charges Q located at (0, y) and (0, -y). A third charge q of the same polarity can move along the x-axis.
Step 2: Analyze the Forces on Charge q
The force on charge q due to each charge Q can be calculated using Coulomb's law. The distance from charge q at position (x,0) to either charge Q is given by:
r=√x2+y2
Step 3: Calculate the Electric Field
The electric field E at position (x,0) due to each charge Q is given by:
E=kQr2=kQx2+y2
where k is Coulomb's constant.
Step 4: Determine the Direction of the Forces
Both charges Q exert forces on q that are directed away from themselves since all charges are of the same polarity. The net electric field E at point (x,0) will be the vector sum of the fields due to both charges.
Step 5: Analyze Equilibrium at the Origin
At the origin (0, 0), the distances to both charges are equal, and the magnitudes of the electric fields due to both charges are equal but in opposite directions. Therefore, the net electric field at the origin is zero:
Enet=EQ1+EQ2=0
Thus, the charge q is in equilibrium at the origin.
Step 6: Determine the Nature of Motion
For any position of charge q along the x-axis (other than the origin), the net force will always point away from the origin. This means that if q is displaced from the origin, it will experience a force that pushes it further away from the origin, indicating that oscillatory motion is impossible.
Step 7: Find the Position of Maximum Force
To find where the force on charge q is maximized, we need to differentiate the expression for the net force F acting on q and set the derivative to zero. The force F can be expressed as:
F=2⋅kQq(x2+y2)3/2⋅x
Differentiating this with respect to x and setting it to zero will yield the condition for maximum force.
Step 8: Solve for Maximum Force Position
After differentiating and simplifying, we find that the maximum force occurs at:
y2=2x2⇒x=±y√2
Conclusion
Based on the analysis:
- The charge q is in equilibrium at the origin.
- The force on q is directed away from the origin for any position other than the origin.
- The force is maximized at x=±y√2.
Final Answer
The correct options are:
- Option A: True (Force is maximum at x=±y√2)
- Option B: True (Charge q is in equilibrium at the origin)
- Option D: True (For any position of q other than the origin, the force is directed away from the origin)
We have two point charges Q located at (0, y) and (0, -y). A third charge q of the same polarity can move along the x-axis.
The force on charge q due to each charge Q can be calculated using Coulomb's law. The distance from charge q at position (x,0) to either charge Q is given by:
r=√x2+y2
The electric field E at position (x,0) due to each charge Q is given by:
E=kQr2=kQx2+y2
where k is Coulomb's constant.
Both charges Q exert forces on q that are directed away from themselves since all charges are of the same polarity. The net electric field E at point (x,0) will be the vector sum of the fields due to both charges.
At the origin (0, 0), the distances to both charges are equal, and the magnitudes of the electric fields due to both charges are equal but in opposite directions. Therefore, the net electric field at the origin is zero:
Enet=EQ1+EQ2=0
Thus, the charge q is in equilibrium at the origin.
For any position of charge q along the x-axis (other than the origin), the net force will always point away from the origin. This means that if q is displaced from the origin, it will experience a force that pushes it further away from the origin, indicating that oscillatory motion is impossible.
To find where the force on charge q is maximized, we need to differentiate the expression for the net force F acting on q and set the derivative to zero. The force F can be expressed as:
F=2⋅kQq(x2+y2)3/2⋅x
Differentiating this with respect to x and setting it to zero will yield the condition for maximum force.
After differentiating and simplifying, we find that the maximum force occurs at:
y2=2x2⇒x=±y√2
Based on the analysis:
- The charge q is in equilibrium at the origin.
- The force on q is directed away from the origin for any position other than the origin.
- The force is maximized at x=±y√2.
The correct options are:
- Option A: True (Force is maximum at x=±y√2)
- Option B: True (Charge q is in equilibrium at the origin)
- Option D: True (For any position of q other than the origin, the force is directed away from the origin)
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension
25 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Integer
8 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct
47 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
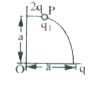
Two point charges q AND 2q are placed at (a,0) and (0,a) A point charge q1 is placed at a P on the quarter circle of radius a as shown in the diagram so that the electric field at the origin becomes zero
View SolutionTwo point charges q each are fixed at (a,0) and (-a,0). A third charge Q is placed at origin. Electrons potential energy of the system will
View SolutionTwo point charges Q and -Q/4 are separated by a distance x.

View SolutionTwo point charges +q and fixed at (a,0,0) and (−a,0,0). A third point charge −q is at origin. State whether ite equlilbrium is stable, unstable or neutral if it is slightly displaced:
(a) along x-axis. , (b) along y-axis.
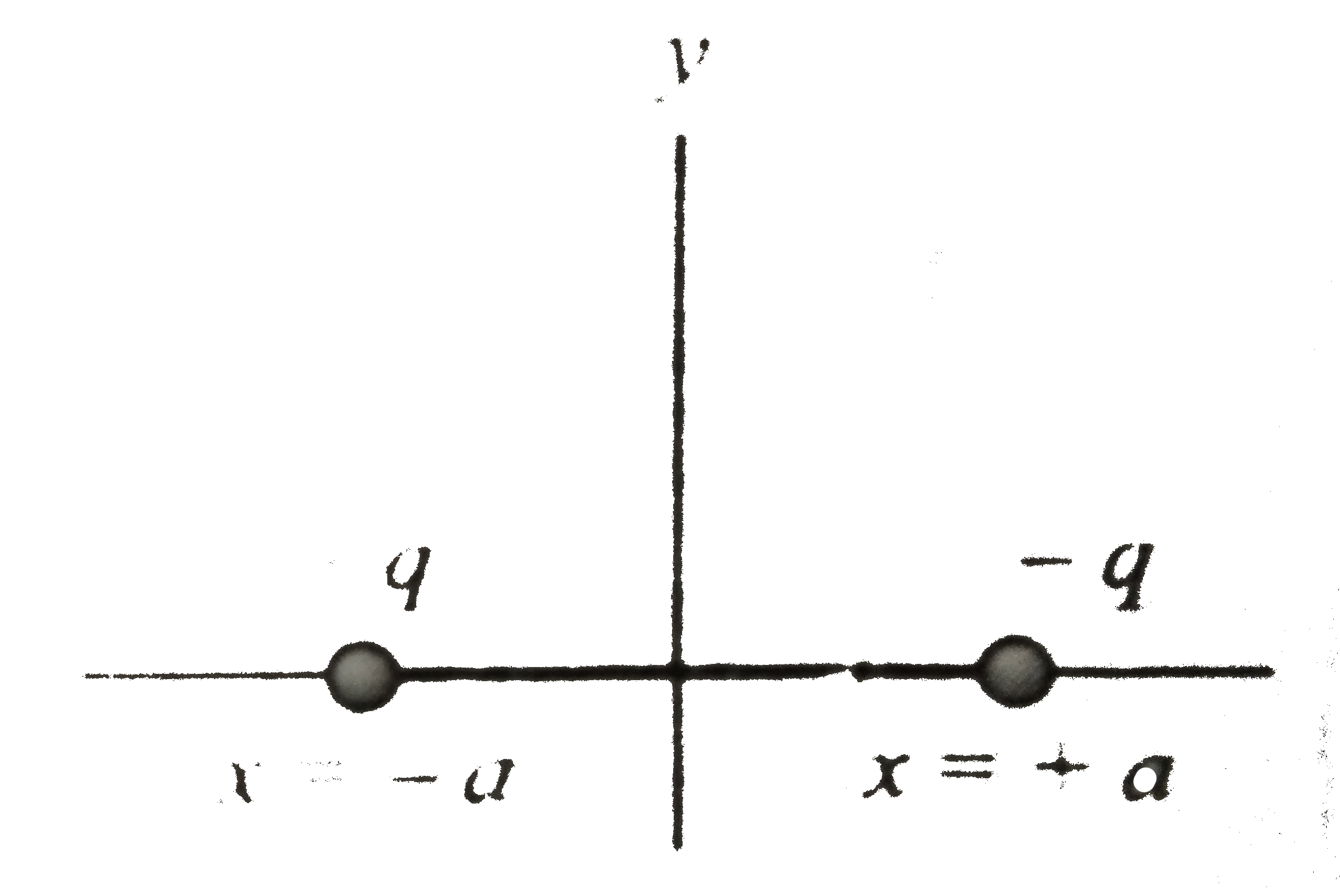
View SolutionTwo point charge ±q are placed on the axis at x=−a and x=+a, as shown in fig.
(i) Plot the variation of E along the x-axis.
(ii) Plot the variation of E along the y-axis.
View SolutionTwo identical charge of value Q each are placed at (-a,0) and (a , 0) . The end coordinates of the point where the net electric field is zero and maximum are respectively-
View SolutionTwo point charge −q and +q/2 are situated at the origin and the point (a,0,0) respectively. The point along the X-axis where the electic field Vanishes is
View SolutionTwo point charges +8q and −2q are located at x=0 and x=L respectively. The location of a point on the x axis at which the net electric field due to these two point charges is zero is
View SolutionA point charge q1=4.00nC is placed at the origin, and a second point charge q2=−3.00nC, placed on the x-axis at x = + 20.0 cm. A third point charge q3=2.00nC is placed on the X-axis between q1,andq2. (Take as zero the potential energy of the three charges when they are infinitely far apart).
(a) What is the potential energy of the system of the three charges if q3 is placed at x= + 10.0 cm?
(b) Where should q3 be placed to make the potential energy of the system equal to zero?
View SolutionElectric potential is a scalar quantity. Due to a point charge charge q at distance r, the potential is given by V=q4π∈0r. A point charge q is placed at (3a,0) and another charge −2q is placed at (−3a,0).
At how many points on the x-axis, (at finite distance) electric potential will be zero?
View Solution
