Two concentric rings, one of radius a and the other of radius b, have the charges +q, and −(2/5)−3/2q, respectively as shown in fig.
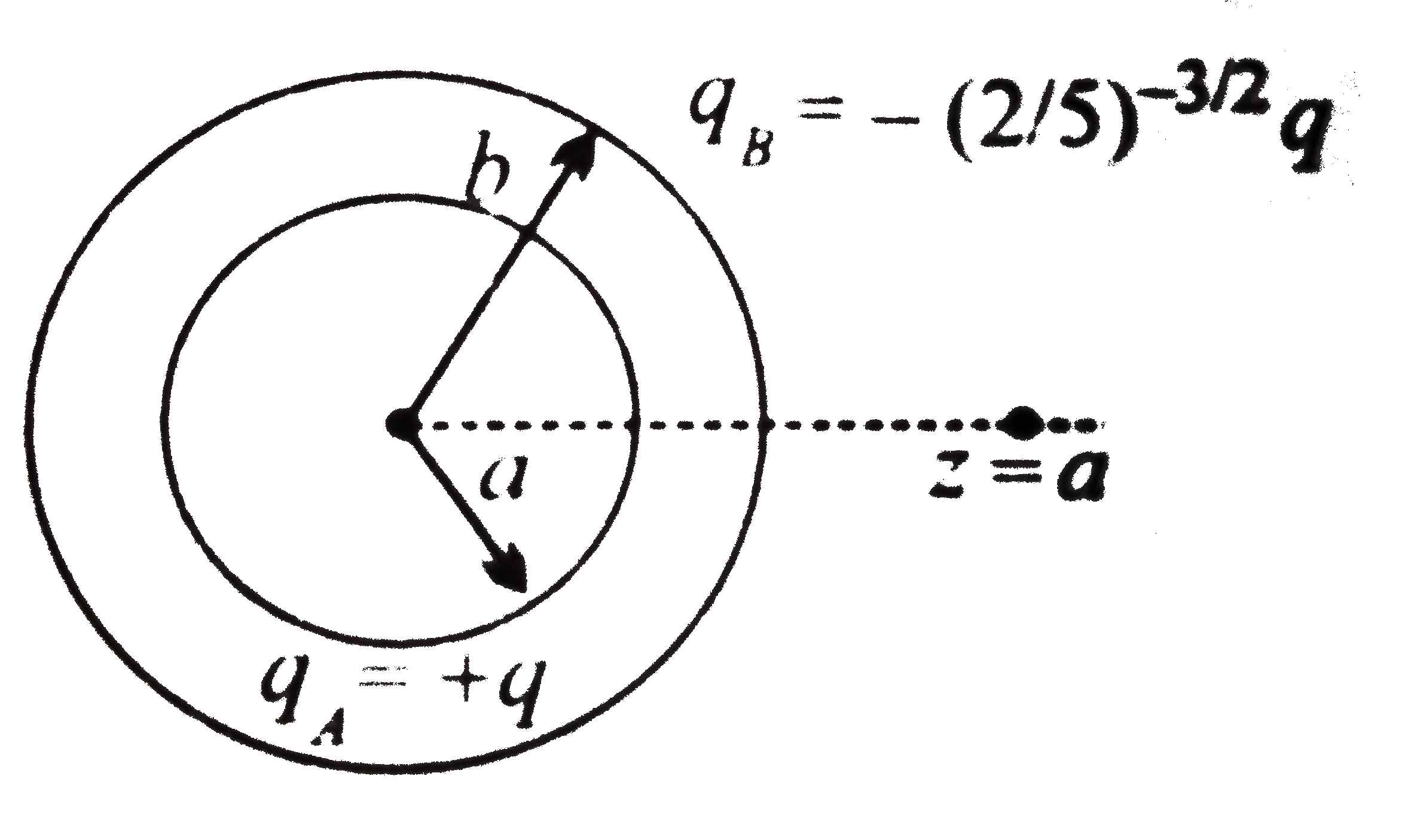
Find the rario b/a if a charge particle palaced on the axis at z =a is i equilibrium.
The correct Answer is:2
For the equilbrium of charge at z=a, the net electric field at this point due to both the rings should be zero.
EA+EB=0⇒kqAa(a2+a2)3/2+kqBa(b2+a2)3/2=0
Put the value and solve to get b/a=2.
Topper's Solved these Questions
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Single Correct Ansewr Type
20 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Multiple Correct Answers Type
2 Videos
- COULOMB LAW AND ELECTRIC FIELDBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - COULOMB LAW AND ELECTRIC FIELDEXERCISE - Comprehension
25 Videos
- CENGAGE PHYSICS DPPBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - CENGAGE PHYSICS DPPEXERCISE - subjective type
51 Videos
- ELECTRIC CURRENT & CIRCUITSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - ELECTRIC CURRENT & CIRCUITSEXERCISE - Kirchhoff s law and simple circuits
15 Videos
Similar Questions
Two concentric conducting shells of radii R and 2R are having charges Q and -2Q respectively.In a region r
View SolutionTwo identical coaxial rings each of radius R are separated by a distance of √3R. They are uniformly charged with charges +Q and −Q respectively. The minimum kinetic energy with which a charged particle (charge +q) should be projected from the centre of the negatively charged ring along the axis of the rings such that it reaches the centre of the positively charged ring is
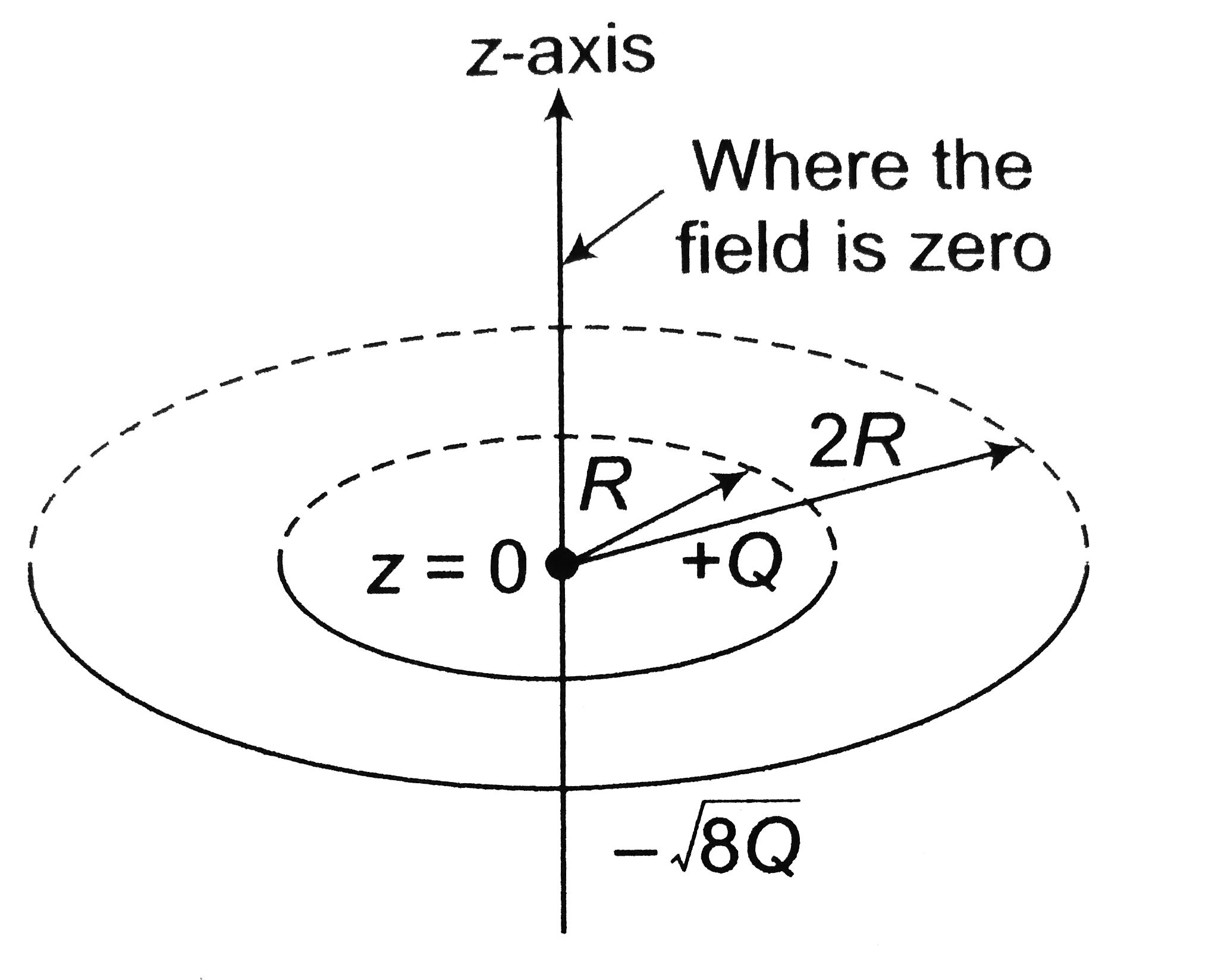
View SolutionTwo concentric rings, one of radius R and total charge +Q and second of radius 2R and total charge −√8Q, lie in x−y plane (i.e., z=0plane). The common centre of rings lies at origin and the common axis coincides with z-axis. The charge is uniformly distributed on both rings.
At what distance from origin is the net electric field on z-axis zero?
View SolutionTwo concentric spherical shells of radius R1 and R2(R2>R1) are having uniformly distributed charges Q1 and Q2 respectively. Find out total energy of the system.

View SolutionCharges Q,2Q, and −Q are given to three concentric conducting sphereical shells A,B and C respectively as shown in figure. The ratio of charge on the inner and outer surface of shell C will be

View SolutionCharges Q,2Q, and −Q are given to three concentric conducting sphereical shells A,B and C respectively as shown in figure. The ratio of charge on the inner and outer surface of shell C will be

View SolutionTwo uniformly charged concentric spherical shells of radius R and r, are given charges Q1 and Q2 respectively. If their potential difference is V, then it will not depends upon:

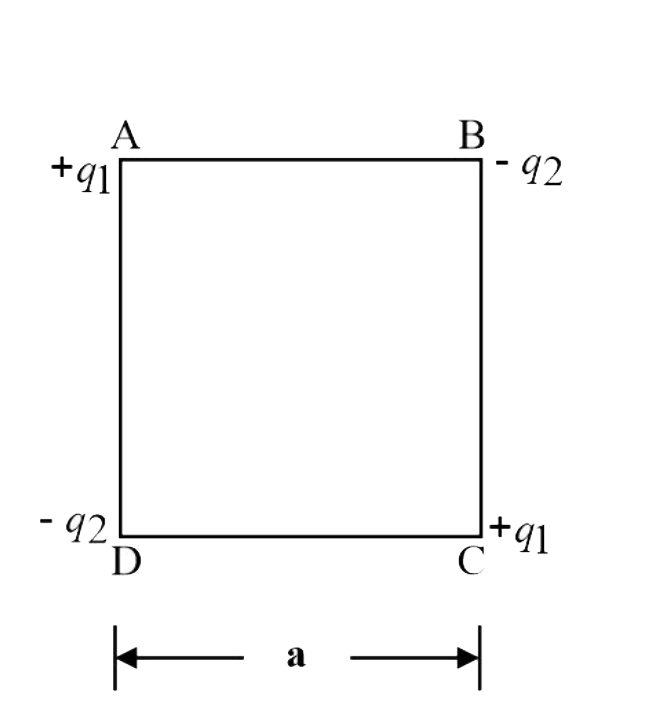
View SolutionCharges are placed at the corners of a square of side a as shown in the following figure. The charged particle placed at A is in equilibrium. The ratio q1q2 is
View SolutionTwo positive charges q1andq2 are moving with velocities v1andv2 when they are at points A and B, respectively, as shown in Fig. The magnetic force experienced by charge q1 due to the other charge q2 is
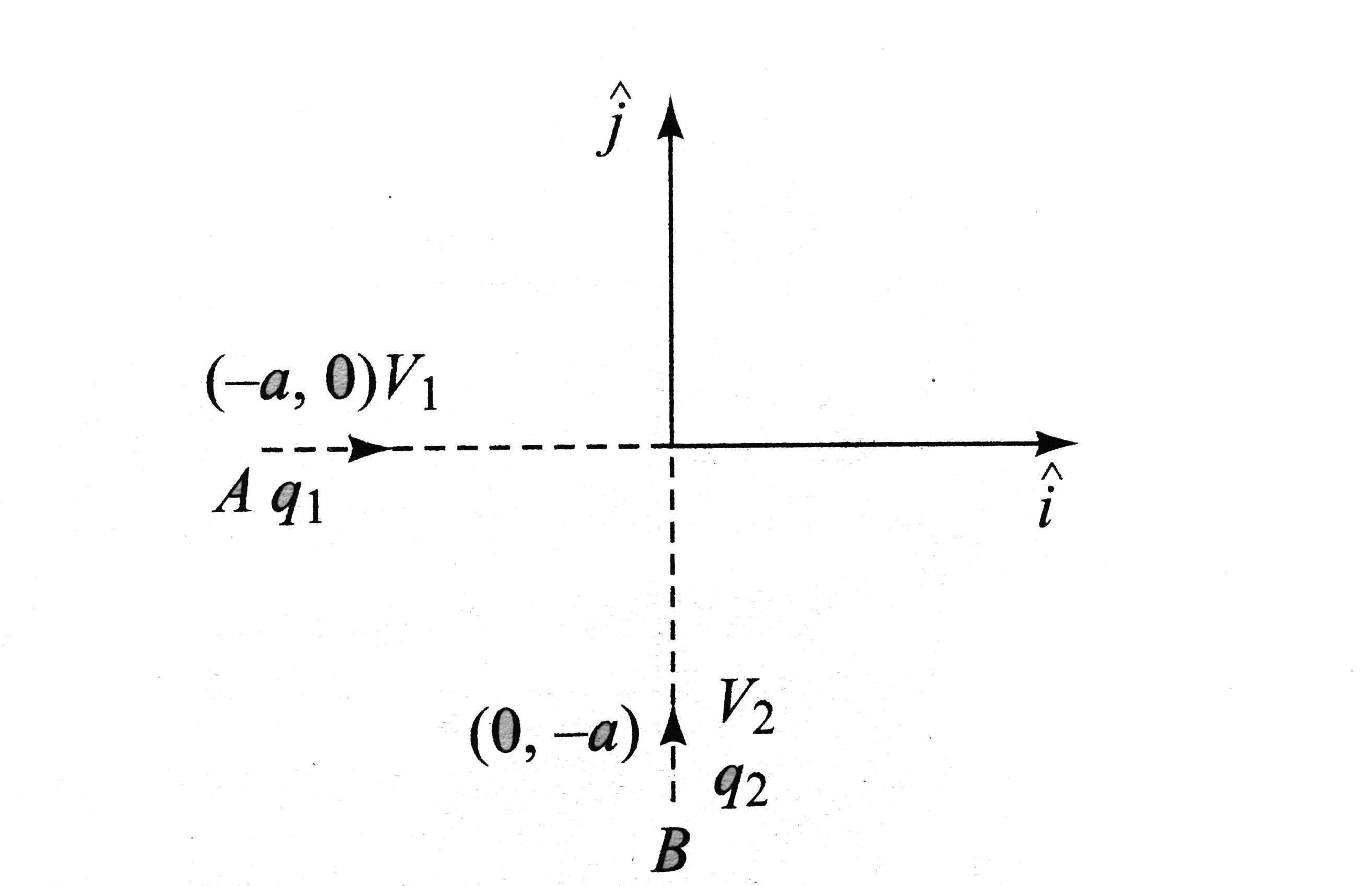
View SolutionAn uncharged conductor of inner radius R1 and outer radius R2 constains a point charge q at the centre as shown in figure
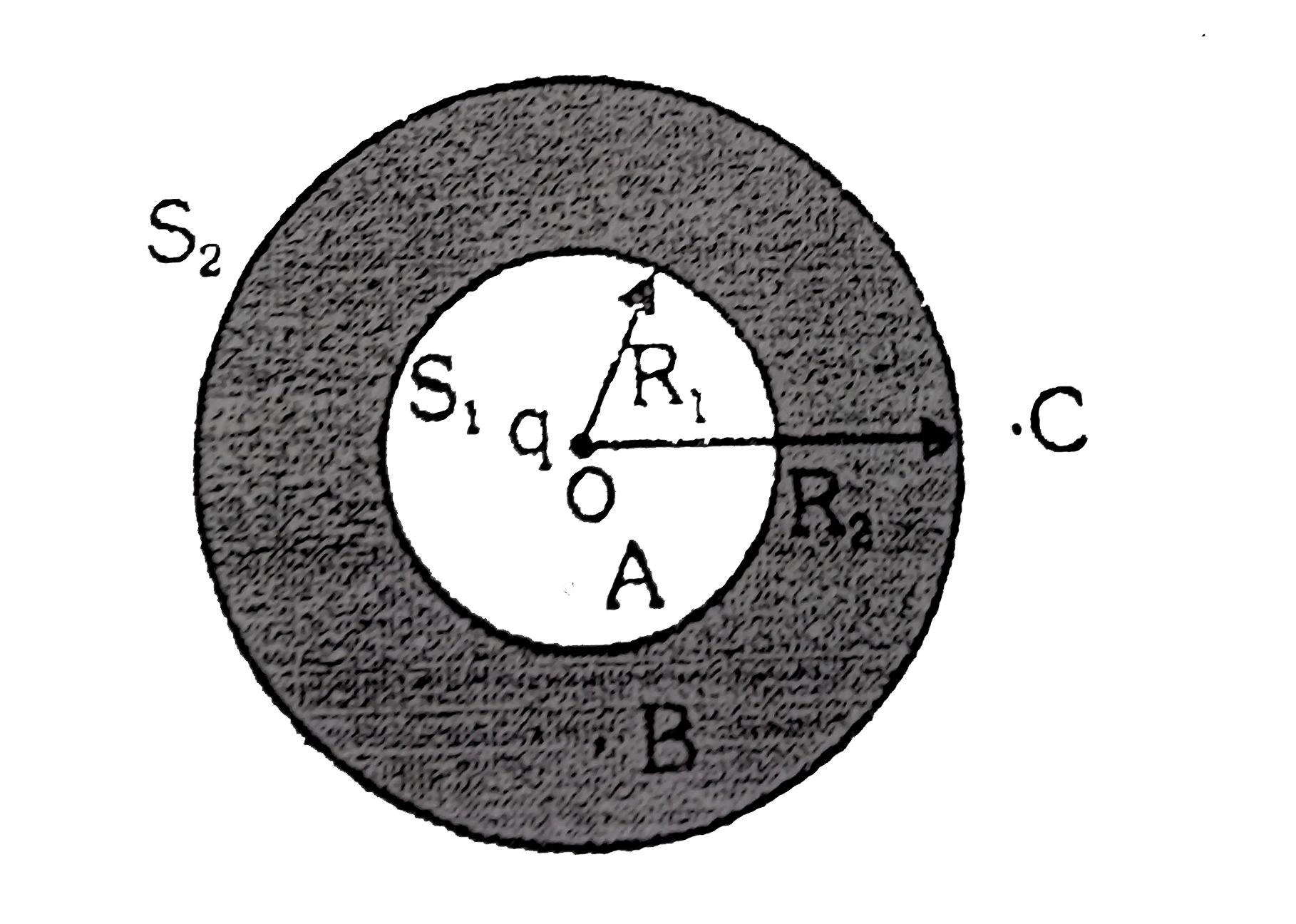
(i) Find →E and V at points A, B and C
(ii) If a pint charge Q is kept out side the sphere at a distance 'r'(>>R2) from centre then find out resultant force on charge Q and charge q.
View Solution
