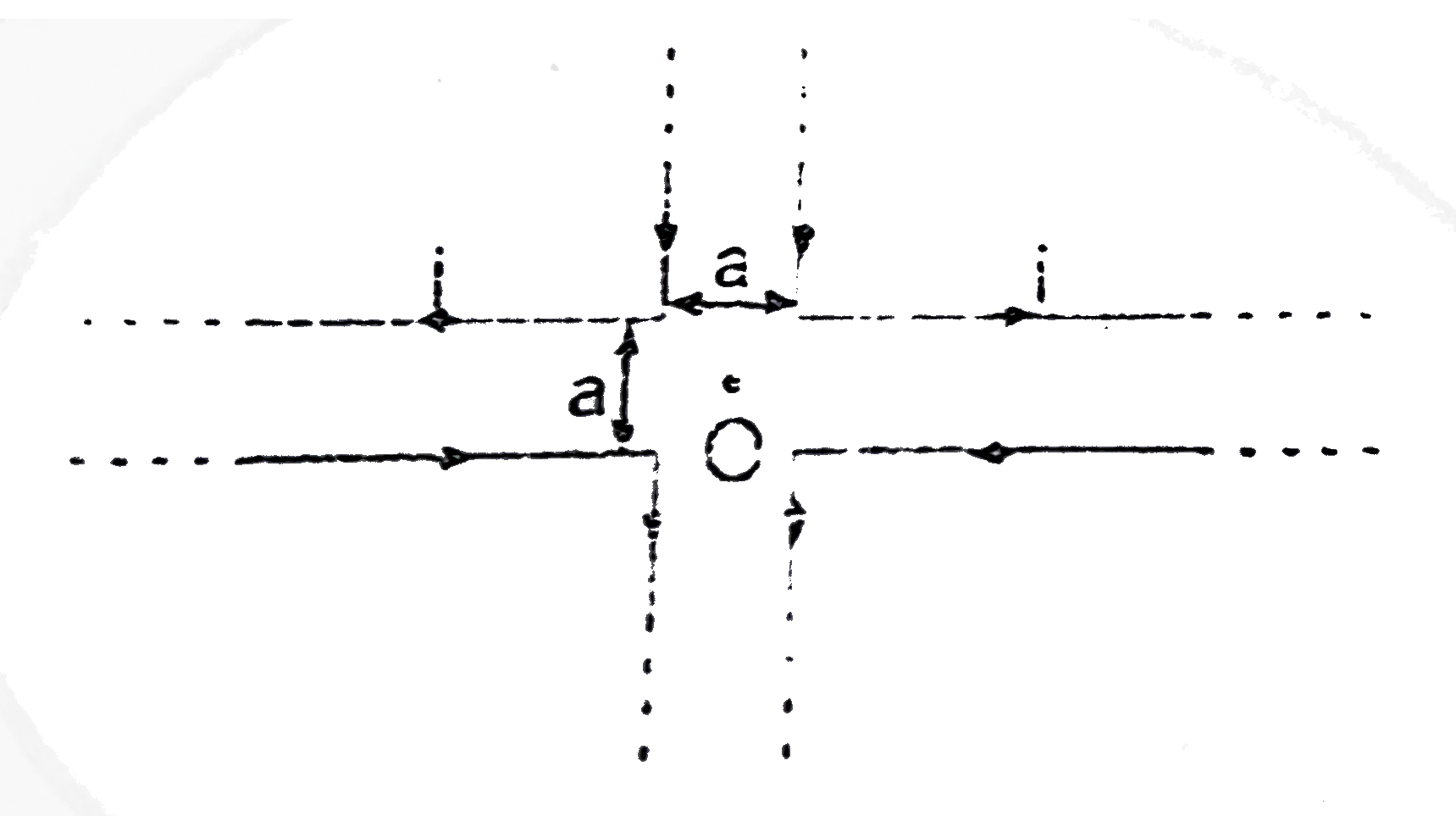
The location of three long wires carrying same current $I$ are $x = - a$ , $x = 0$ and $x = +$ a respectively as shown in figure. The magnetic field at point ( $0$ , $0$ , $a$ ) is

A

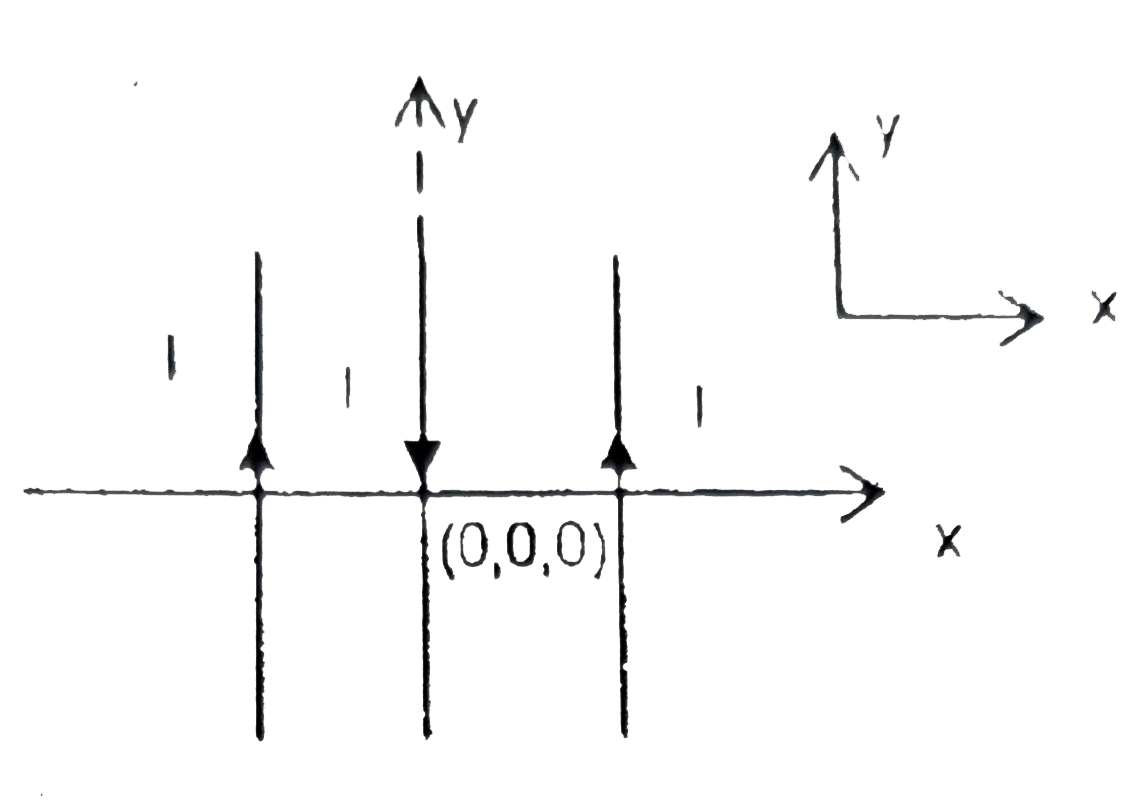
$\frac{μ_{0} I}{2 π a}$

B

$\frac{μ_{0} I}{\sqrt{2} π a}$

C

$\frac{μ_{0} I}{2 \sqrt{2} π a}$

D

zero

Video Solution

Text Solution

Verified by Experts

By symmetry, the net field is Zero
The net field at $P (0, 0, a)$
$\to B = {\to B}_{A} + {\to B}_{0} + {\to B}_{c}$
$= \frac{μ_{0} I}{2 π a \sqrt{2}} {{cos 45}^{\circ} ˆ i + {sin 45}^{\circ} (- ˆ k)} + \frac{μ_{0} I}{2 π a} (- ˆ i) + \frac{μ_{0} I}{2 π a \sqrt{2}} {{cos 45}^{\circ} ˆ i + {sin 45}^{\circ} (ˆ k)}]$
$= \frac{μ_{0} I}{2 π a \sqrt{2}} \sqrt{2} ˆ i + \frac{μ_{0} I}{2 π a} (- ˆ i)$
$= \frac{μ_{0} I}{2 π a} [ˆ i - ˆ i] = 0$

Updated on:21/07/2023

|

Class 12 PHYSICS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile