Two long straight parallel wires, carrying (adjustable) currents I1 and I2 are kept at a distance d apart. If the force F between the two wires is taken as positive when the wire repel each other and negative when the wires attract each other, the graph showing the dependence of F, on the product I1I2 would be:
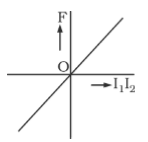
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the force F between two parallel wires carrying currents I1 and I2, and the product I1I2.
1. Understanding the Force Between Wires:
The force per unit length F/L between two long parallel wires carrying currents I1 and I2 is given by the formula:
FL=μ0I1I22πd
where μ0 is the permeability of free space and d is the distance between the wires.
2. Direction of the Force:
- If the currents I1 and I2 are in the same direction, the wires will repel each other, leading to a positive force F.
- If the currents are in opposite directions, the wires will attract each other, resulting in a negative force F.
3. Expressing the Force:
Based on the previous understanding, we can express the force F as:
F=μ0I1I22πdL
Here, L is the length of the wires, and we can see that F is directly proportional to the product I1I2.
4. Considering the Sign:
- When I1I2>0 (currents in the same direction), F is positive (repulsion).
- When I1I2<0 (currents in opposite directions), F is negative (attraction).
5. Graphing the Relationship:
- The graph of F versus I1I2 will be a straight line.
- The slope of the line will be positive when I1I2>0 and negative when I1I2<0.
- Therefore, the graph will cross the origin and will have a negative slope in the region where I1I2<0.
6. Conclusion:
The correct graph showing the dependence of F on the product I1I2 will be a straight line that is positive for I1I2>0 and negative for I1I2<0.
Final Answer:
The graph will be a straight line with a negative slope, indicating that F is directly proportional to I1I2 but with a sign change depending on the direction of the currents.
The force per unit length F/L between two long parallel wires carrying currents I1 and I2 is given by the formula:
FL=μ0I1I22πd
where μ0 is the permeability of free space and d is the distance between the wires.
- If the currents I1 and I2 are in the same direction, the wires will repel each other, leading to a positive force F.
- If the currents are in opposite directions, the wires will attract each other, resulting in a negative force F.
Based on the previous understanding, we can express the force F as:
F=μ0I1I22πdL
Here, L is the length of the wires, and we can see that F is directly proportional to the product I1I2.
- When I1I2>0 (currents in the same direction), F is positive (repulsion).
- When I1I2<0 (currents in opposite directions), F is negative (attraction).
- The graph of F versus I1I2 will be a straight line.
- The slope of the line will be positive when I1I2>0 and negative when I1I2<0.
- Therefore, the graph will cross the origin and will have a negative slope in the region where I1I2<0.
The correct graph showing the dependence of F on the product I1I2 will be a straight line that is positive for I1I2>0 and negative for I1I2<0.
The graph will be a straight line with a negative slope, indicating that F is directly proportional to I1I2 but with a sign change depending on the direction of the currents.
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 2
50 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
When two parallel wires carrying current l and 2l in same direction are placed at a distance d apart, the ratio of force per unit length acting upon the wire due to other is
View SolutionTwo long straight wires, each carrying a current I in opposite directions are separated by a distance R. The magnetic induction at a point mid way between the wire is
View SolutionTwo long straight parallel conductors carry steady current I1 and I2 separated by a distance d. if the currents are flowing it the same direction show how that magnetic field st up in one produces an attractive force on the other . Obtain the expression for this force. Hence define one ampere.
View SolutionTwo long parallel wires carry equal current I flowing in the same direction are at a distance 2d apart. The magnetic field B at a point lying on the perpendicular line joining the wires and at a distance x from the midpoint is
View SolutionTwo long parallel copper wires carry current of 5A each in opposite directions. If the wires are separated by a distance distance of 0.5m, then the force per unit length between the two wires is
View SolutionTwo infinitely long straight parallel wires carry equal currents 'I' in the same direction and are 2 m apart. Magnetic induction at a point which is at same normal distance (√2)m from each wire has magnitude
View SolutionForce per unit length acting at one end of each of the two long parallel wires, carrying current I each, kept distance r apart is
View SolutionEach of two long parallel wires carries a constant current i along the same direction . The wires are separated by a distance 2I. The magnitude of resultant magnetic induction in the symmetric plane of this system located between the wires at a distance R from each wire will be
View SolutionTwo long parallel wires are at a distance of 1 m. Both of them carry 1A of current. The force of attraction per unit length between the two wires is
View SolutionTwo long wires, carrying currents i1andi2, are placed perpendicular to each other in such a way that they just avoid a contact. Find the magnetic force on a small length dl of the second wire situated at a distance l from the first wire. (figure)

View Solution
