A current loop ABCD is held fixed on the plane of the paper as shown in the figure. The arcs BC (radius = b) and DA radius = a) of the loop are joined by two straight wires AB and CD. A steady current I is flowing in the loop. Angle made by AB and CD at the origin O is 30∘. Another straight thin wire with steady current I1 flowing out of the plane of the paper is kept at the origin.
Zero
μ0I(b−a)24ab
μ0I4π[b−aab]
μ0I4π[2(b−a)+π3(a+b)]
The correct Answer is:B
To find the magnitude of the magnetic field B at the origin O due to the current loop ABCD, we will analyze the contributions from different sections of the loop.
Step 1: Analyze the Current Loop
- The current loop consists of two arcs (BC and DA) and two straight wires (AB and CD).
- The angle between the wires AB and CD at the origin O is 30∘.
Step 2: Magnetic Field Due to Arc DA
- The magnetic field BDA at the origin due to the arc DA can be calculated using the formula:
BDA=μ0I4πa⋅θ
where θ is the angle in radians.
- Convert 30∘ to radians:
θ=30×π180=π6 radians
- Substitute θ into the formula:
BDA=μ0I4πa⋅π6=μ0I24a
- The direction of BDA is upward.
Step 3: Magnetic Field Due to Arc BC
- Similarly, the magnetic field BBC at the origin due to the arc BC is given by:
BBC=μ0I4πb⋅θ
- Using the same angle θ=π6:
BBC=μ0I4πb⋅π6=μ0I24b
- The direction of BBC is downward.
Step 4: Magnetic Field Due to Straight Wires AB and CD
- The straight wires AB and CD do not contribute to the magnetic field at the origin because they are aligned along the line OA and do not create a magnetic field at that point.
Step 5: Calculate the Net Magnetic Field
- The net magnetic field Bnet at the origin is the vector sum of the contributions from the arcs:
Bnet=BDA−BBC=μ0I24a−μ0I24b
- Factor out μ0I24:
Bnet=μ0I24(1a−1b)
Step 6: Final Expression
- Thus, the final expression for the magnetic field at the origin is:
Bnet=μ0I24(b−aab)
- The direction of the net magnetic field is upward (out of the plane of the paper).
- The current loop consists of two arcs (BC and DA) and two straight wires (AB and CD).
- The angle between the wires AB and CD at the origin O is 30∘.
- The magnetic field BDA at the origin due to the arc DA can be calculated using the formula:
BDA=μ0I4πa⋅θ
where θ is the angle in radians.
- Convert 30∘ to radians:
θ=30×π180=π6 radians
- Substitute θ into the formula:
BDA=μ0I4πa⋅π6=μ0I24a
- The direction of BDA is upward.
- Similarly, the magnetic field BBC at the origin due to the arc BC is given by:
BBC=μ0I4πb⋅θ
- Using the same angle θ=π6:
BBC=μ0I4πb⋅π6=μ0I24b
- The direction of BBC is downward.
- The straight wires AB and CD do not contribute to the magnetic field at the origin because they are aligned along the line OA and do not create a magnetic field at that point.
- The net magnetic field Bnet at the origin is the vector sum of the contributions from the arcs:
Bnet=BDA−BBC=μ0I24a−μ0I24b
- Factor out μ0I24:
Bnet=μ0I24(1a−1b)
- Thus, the final expression for the magnetic field at the origin is:
Bnet=μ0I24(b−aab)
- The direction of the net magnetic field is upward (out of the plane of the paper).
Topper's Solved these Questions
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - JEE Advanced (Archive)
78 Videos
- MAGNETIC EFFECTS OF CURRENT BOOK - VMC MODULES ENGLISHCHAPTER - MAGNETIC EFFECTS OF CURRENT EXERCISE - LEVEL 2
50 Videos
- LIQUIDSBOOK - VMC MODULES ENGLISHCHAPTER - LIQUIDSEXERCISE - JEE ADVANCED (LEVEL -2)
55 Videos
- MOCK TEST 1BOOK - VMC MODULES ENGLISHCHAPTER - MOCK TEST 1EXERCISE - PART I : PHYSICS (SECTION-2)
10 Videos
Similar Questions
A loop, carring a current i, lying in the plane of the paper, is in the field of a long straight wire with current i0 (inward) as shown in Fig. Find the torque acting on the loop.

View SolutionA square loop is placed near a long current carrying straight wire as shown in the figure . Match the following table


View SolutionA current carrying squre loop is placed near an infinitely long current carrying wire as shown in figure . The loop torque acting on the loop is
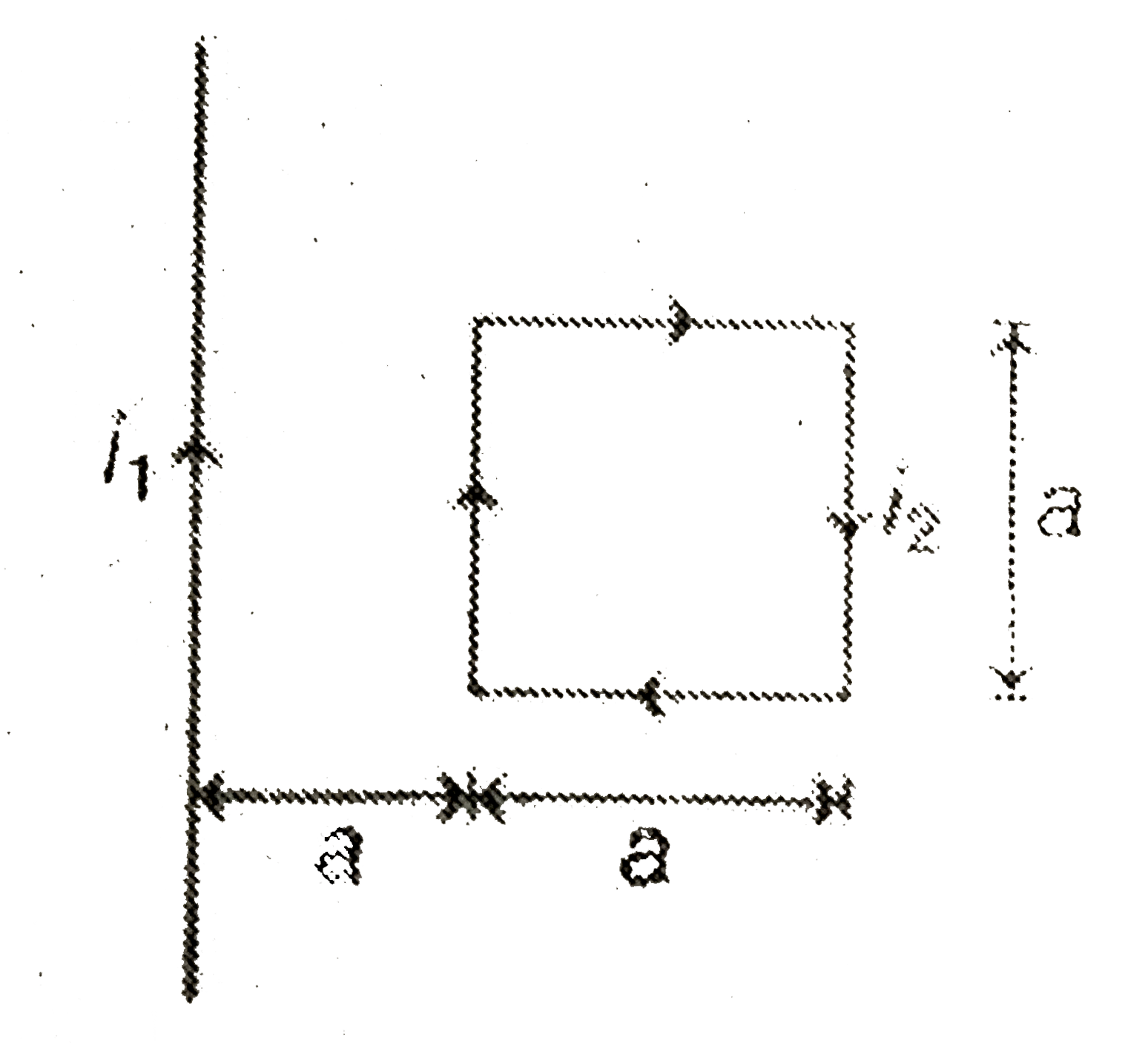
View SolutionA long current carrying wire, carrying current such that it is flowing out from the plane of paper, is placed at O. A steady state current is flowing in the loop ABCD. Then,

View SolutionA wire is bent in the form of a circular arc with a straight portion AB. Magnetic induction at O when current flowing in the wire, is

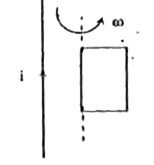
View SolutionA rectangular loop is placed near a current carrying straight wire as shown in the figure. If the loop is rotated about an axis passing throught one of its sides find the direction of induced current in the loop.
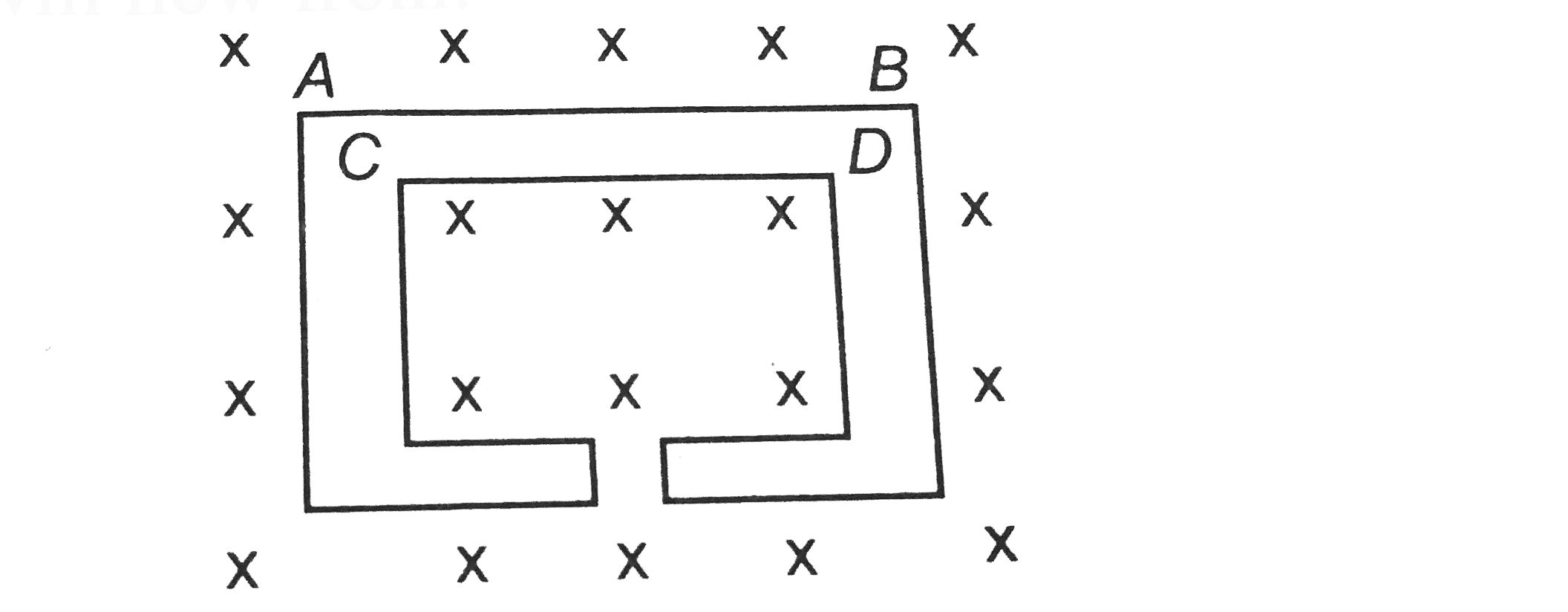
View SolutionA wire is bent to form the double loop shown in figure. There is a uniform magnetic field directed into the plane of the loop. If the magnitude of this field is decreasing current will flow from:
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.
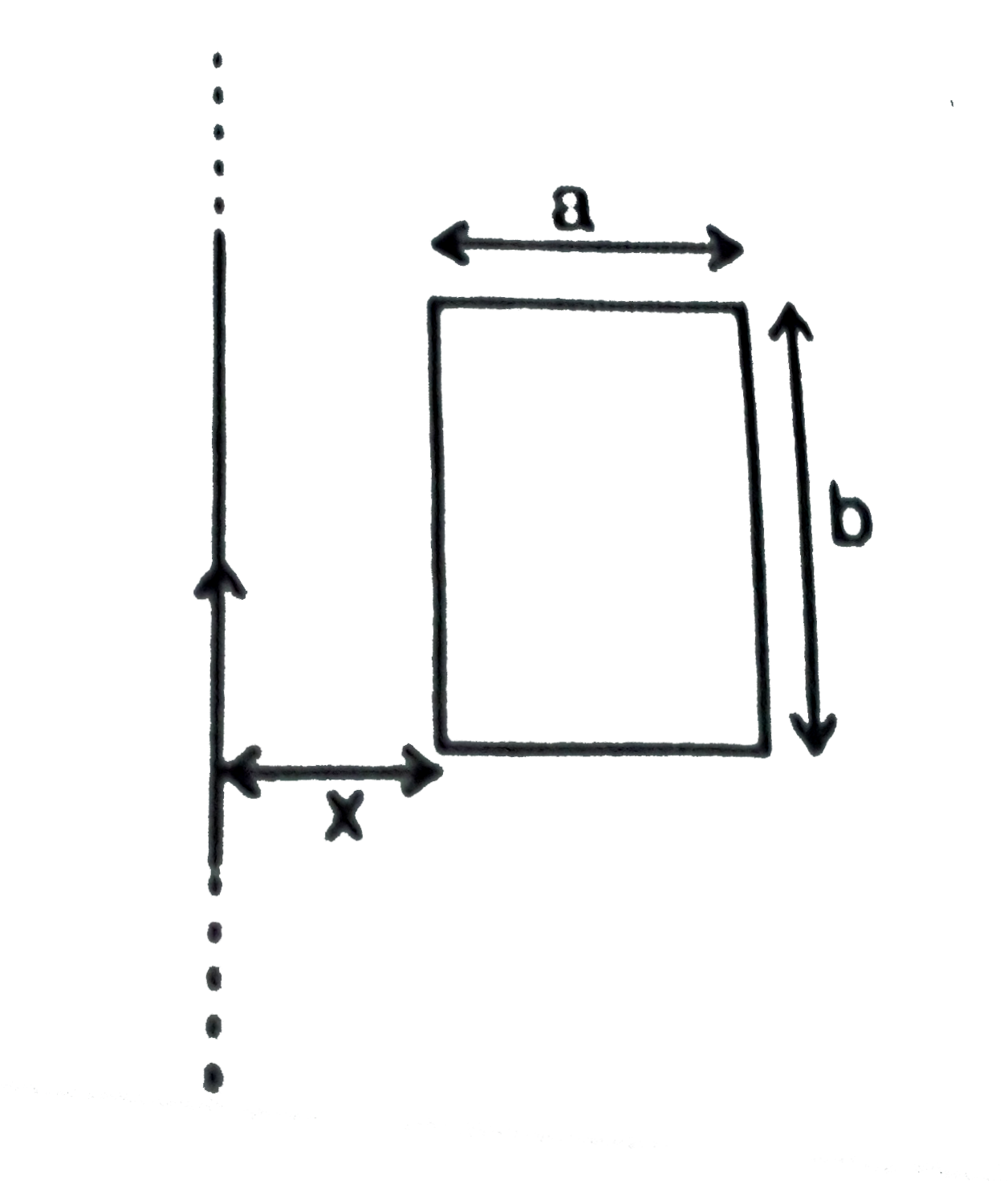
View SolutionFind the mutual inductance of a straight long wire and a rectangular loop, as shown in the figure.

View SolutionConsider the situation shown in figure. If the current I in the long straight wire xy is increased at a steady rate the induced current in loop A and B will be
View Solution
