Two parallel pltate capacitors A and B have the same separation d=8.85×10−4m between the plates. The plate areas of A and B are 0.04m2 and 0.02m2, respectively. A slab of dielectric constant (relative permittivity) K=9 has dimensions such that it can exactly fill the space between the plates of capacitor B.
 .
.
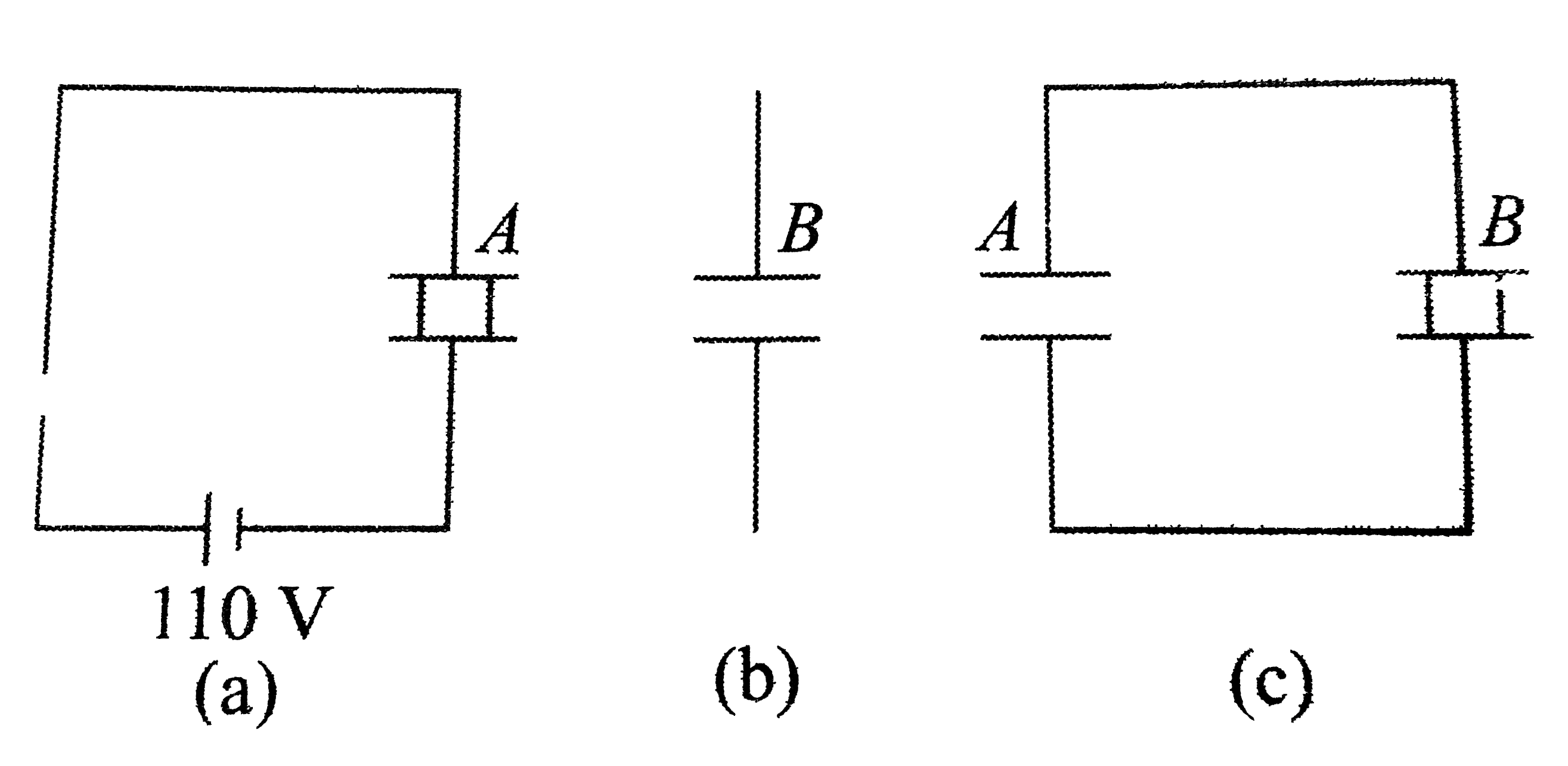
i. The dielectric slab placed insid A as shown in. A is then charge to a potential difference of 110V.Calca––tethe∩acitanceofAandthee≠rgys→red∈it.<br>ii.Thebaeryisdisco∩ected,andthenthedie≤ctricslabisremovedomAF∈dtheworkdo≠bytheextergya≥ncy∈remov∈gtheslabomA.<br>iii.Thesamedie≤ctricslabisnowplaced∈sB,fill∈gitcomp≤tely.Thetwo∩ci→rsA and Barethenco∩ectedasshown∈.(c ). Calculate the energy stored in the system.
(i) capacitor A is a combination of two capacitor CK and C0 in parallel.Hence,
CA=CK+C0=Kε0Ad+ε0Ad=(K+1)ε0Ad
Here, A=0.22m2 Substituting the values,we have
CA=(9+1)8.85×10−12(0.02)(8.85×10−4)CA=2.0×10−9F
Energy stored in capacitor,A when connected with a 110V battery is
UA=12CAV2=12(2×10−9)(110)2UA=1.21×10−5J
Charge stored in the capacitor, qA=CAV(2.0×10−9)(110)qA=2.2×10−7C
Now,this charge remains constant even after battry is disconnected but when the slab is removed.
Capacitance of A will get reduced. Let be C'A
C'A=ε0(2A)d=(8.85×10−128.85×10−4)C'A=0.4×10−9F Energy stored in this case would be
U'A=12(qA)2C'A=12⎛⎝(2.2×10−7)2(0.4×10−9)⎞⎠U'A=6.05×10−5J<UA
Therefore, work done to remove the slab would be
W=U'A−UA=(6.05×1.21)×10−5JorW=4.84×10−5J
(iii) Capacity of B when filled with dielectric ,CB=Kε0Ad=(9)(8.85×10−12)(0.02)(8.85×10−4)
CB=1.8×10−9F, Thes two capacis are in parallel,therefore,net capacitance of the system is
C=C'A+CB=(0.4+1.8)×10−9FC=2.2×10−9F , Change stored in the system is q=qA−2.2×10−7C
Threfore,energy stored,U=12q2C,U=12(2.2×10−7)2(2.2×10−9)orU=1.1×10−5J
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 36
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 37
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 34
1 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
Two parallel plate capacitors A and B have the same separation d=8.85×10−4m between the plates. The plate area of A and B are 0.04m2 and 0.02m2 respectively. A slab of dielectric constant (relative permittivity) K=9 has dimensions such that it can exactly fill the space between the plates of capacitor B.
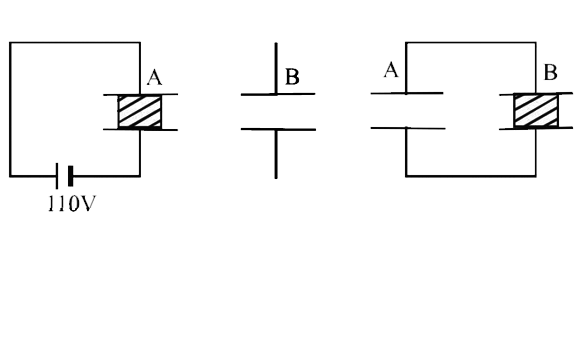
(i) The dielectric slab is placed inside. A as shown in figure (a). A is then charged to a potential difference of 110V. Calculate the capacitance of A and the energy stored in it.
The battery is disconnected and then the dielectric slab is moved from A. Find the work done by the external agency in removing the slab from A.
(iii) The same dielectric slab is now placed inside B, filling it completely, The two capacitors A and B are then connected as shown in figure(c). Calculate the energy stored in the system.
View SolutionHalf of the space between the plates of a parallel plate capacitor is filled with dielectric material of constant K. Then which of the plots are possible?
View SolutionA parallel plate capacitor is connected across a battery. Now, keeping the battery connected, a dielectric slab is inserted between the plates. In the process,
View SolutionA parallel plate capacitor having capacitance 12pF is charged bya battery to a potential difference of 10V between its plates. The charging battery is now disonnected and a porcelain slab of dielectric constant 6.5 is slipped between the plates. The work done by the capacitor on the slab is
View SolutionThe plates of a parallel plate capacitor are charged up to 200 V. A dielectric slab of thickness 4 mm is inserted between its plates. Then, to maintain the same potential difference between the plates of the capacitor, the distance between the plates increased by 3.2 mm. The dielectric constant of the dielectric slab is
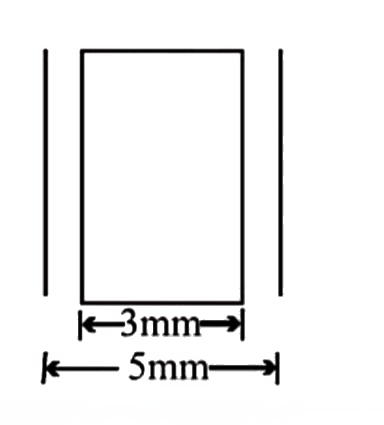
View SolutionSeparation between the plates of parallel plate capacitor is 5 mm. this capacitor, having air as the dielectric medium between the plates, is charged to a potential difference 25 V using a battery. The battery is then disconnected and a dielectric slab of thickness 3mm and dielectric constant K=10 is placed between the plates as shown. potential difference between the plates after the dielectric slab has been introduced is-
View SolutionA dielectric slab is inserted between the plates of an isolated capacitor. The force between the plates will
View SolutionIn the figure shown capacitors A and B of capacitance C are in steady state. A dielectric slab of dielectric constant K=2 and dimensions equal to the inner dimensions of the capcitors is inserted in the space between the plate of the capacitor B. In steady state choose the correct options.
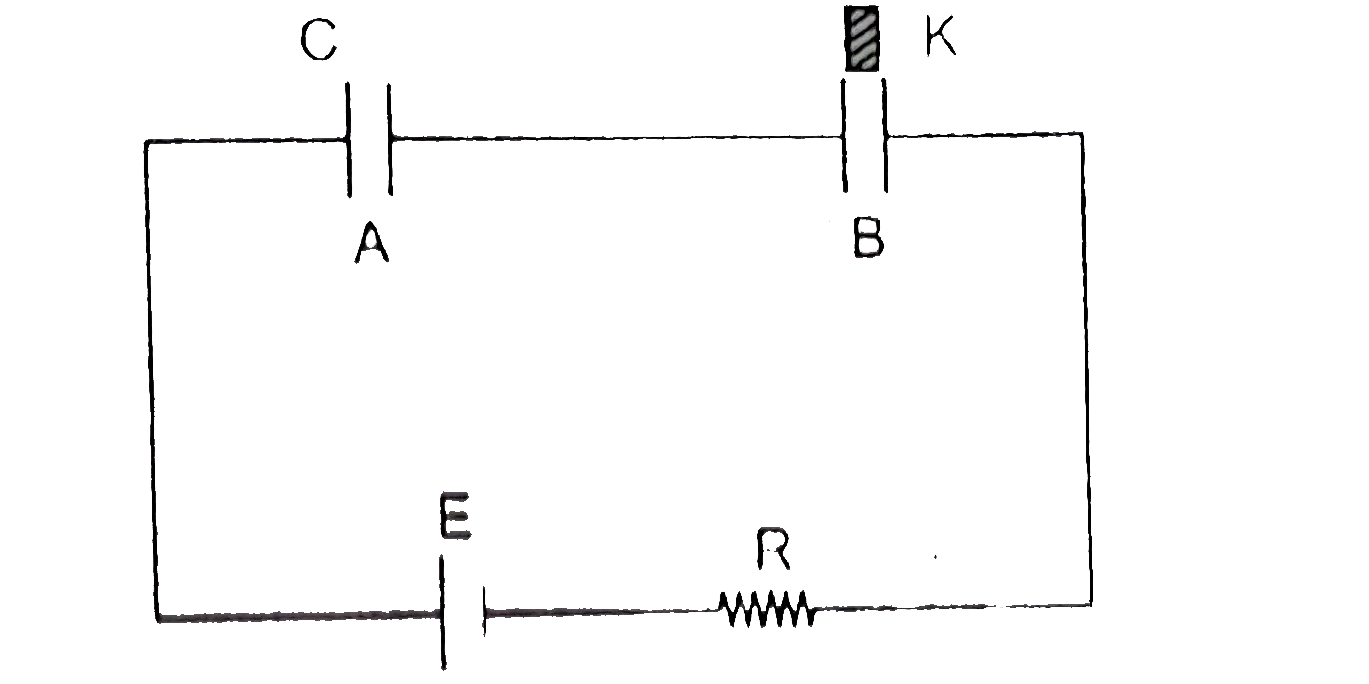
View SolutionAn air-cored capacitor of plate area A and separation d has a capacity C. Two dielectric slabs are inserted between its plates in two different manners as shown. Calculate the capacitance in each case.

View SolutionA parallel - plate capacitor of plate area A and plate separation d is charged to a potential difference V and then the battery is disconnected . A slab of dielectric constant K is then inserted between the plate of the capacitor so as to fill the space between the plate .Find the work done on the system in the process of inserting the slab.
View Solution
