
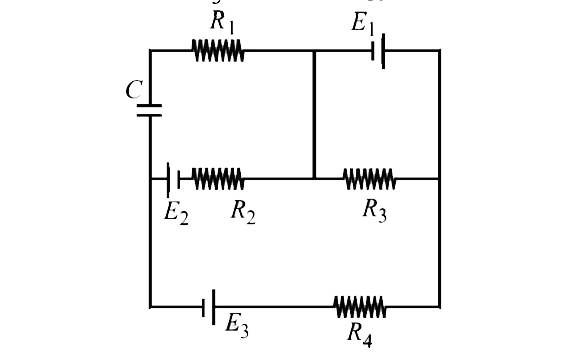
In the circuit shown in figure. ε1=3,ε2=2,ε3=6V,R1=2,R4=6Ω,R3=2,R2=4ΩandC=5μF. Find the current in the resistor R3 and the electrical energy stored in the capacitor C.
The correct Answer is:(I) 1.5
(II) 14.4
In steady state no current will flow through R1=6Ω Potential difference across R3 or 4Ω is E1 or 6V
Current through it will be 64=1.5A from right to left.Because left hand side of this resistance is at higher potential .Now,suppose this 1.5A distributes in i2 as shown applying Kichhoff's second law in loop dhfed
3−3i1−4×1.5−2i1+2=0∴i1=−15A=−0.2A
To find energy stored in capacitor we will have to find potential difference across it or Vad
Now, Va−2i1+2=VdorVa−Vd=2i1−2=−2.4V
or Vd−Va=−2.4V=Vda
Energy stored in capacitor .U=12CV2da=12(5×10−6)(2.4)2=1.44×10−5J=14.4μJ

Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 35
1 Video
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 36
1 Video
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 33
1 Video
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
In the given circuit
E1=3E2=2E3= 6 volts R1=2R4=6Ω
R3=2R2=4Ω C=5μf.
Find the current in R and the energy stored in the capacitor.
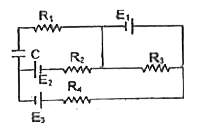
View SolutionIn the given circuit. E1=6vo<s,E2=2vo<s,E3=6vo<s
R1=6ΩR2=2ΩR3=4Oemga,R4=3Ω and C=5μF. Find the current in R3 and energy stored in the capacitor at steady state
View SolutionIn the circuit shown in figure ,(ε)1=3V,(ε)2=2V,(ε)3=1Vandr1=r2=r3=1(Ω).Find the potential difference between the points A and B and the current through each branch.

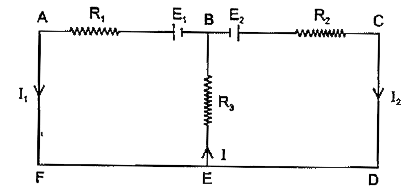
View SolutionIn the circuit shown below, E1=17V,E2=21V,R1=2Ω,R2=3ΩandR3=5Ω. Using Kirchhoff.s laws, find the currents flowing through the resistors R1,R2 and R3. (Internal resistance of each of the batteries is negligible.)
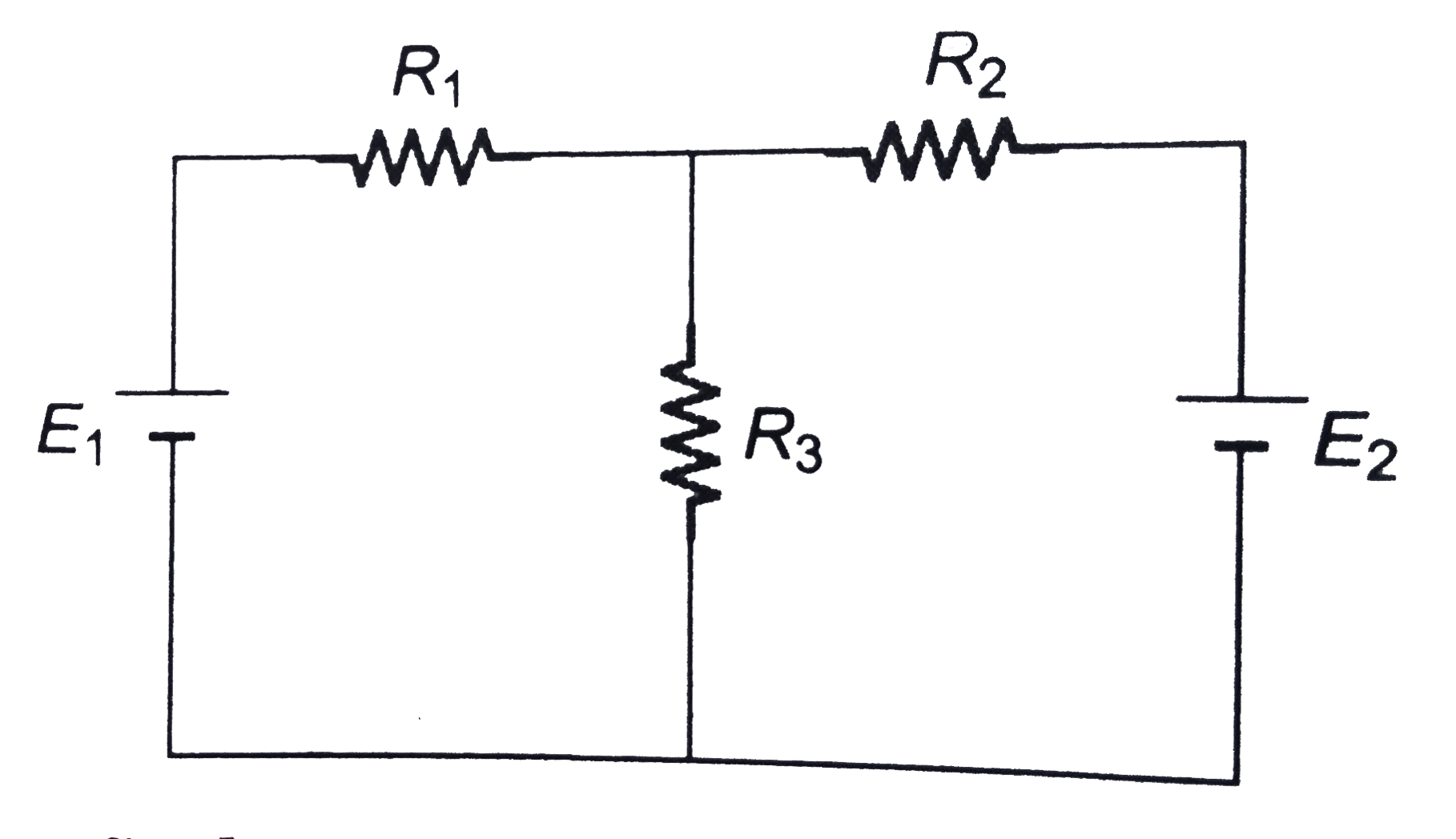
View SolutionIn the circuit shown in figure E1=7V,E2=1V,R1=2Ω,R2=2Ω and R3=3Ω respectively. Find the power supplied by the two batteries.
View SolutionCalculate the effective resistance between the points A and B in the circuit shown in Fig.
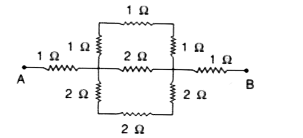
View SolutionFind the currents going through the three resistors R1,R2 and R3 in the circuit of figure.

View SolutionIn the circuit shown in figure

Current through R2 is zero if R4=2Ω and R3=4Ω In this case
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
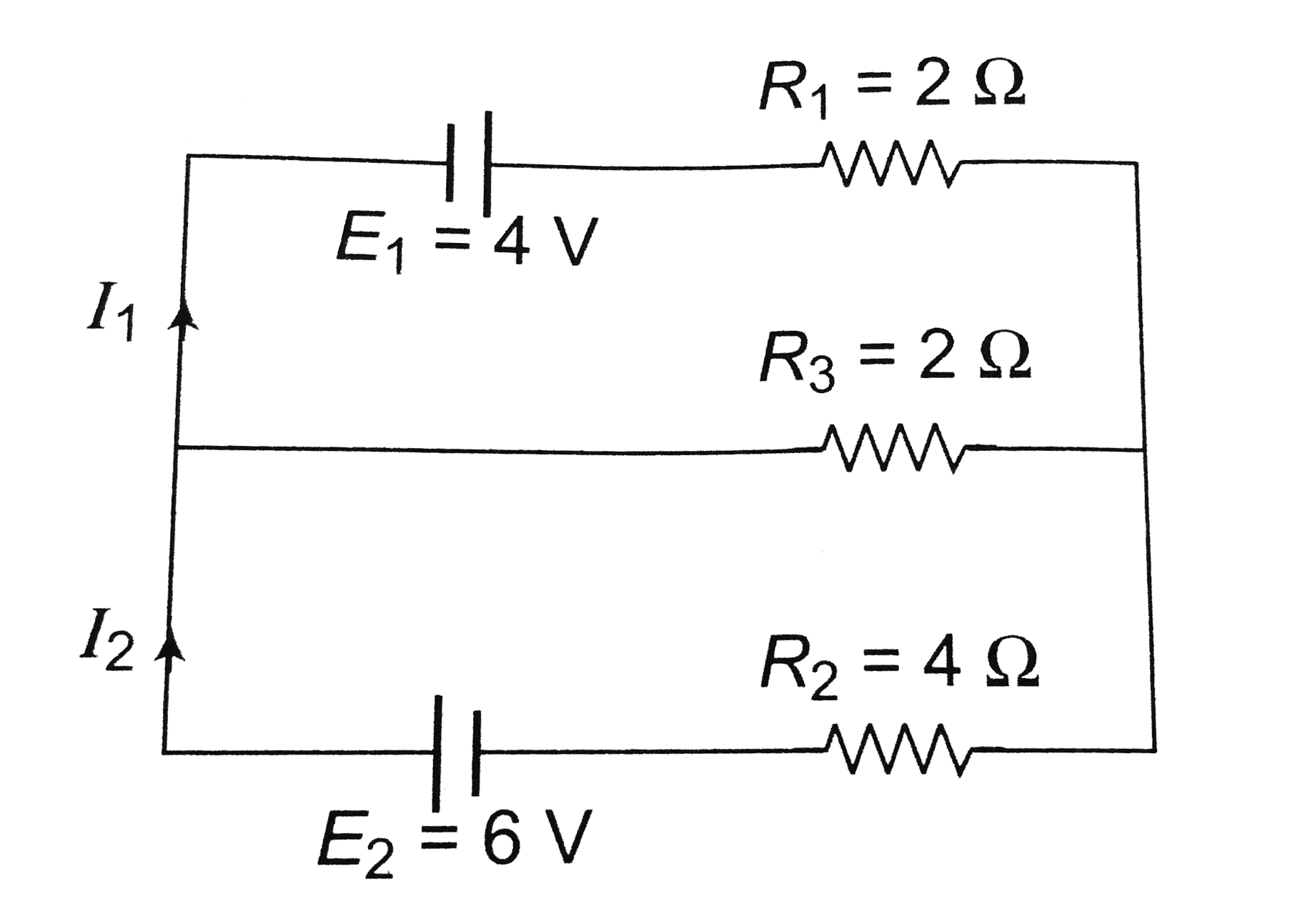
View SolutionIn the circuit shown in fig. R1=10Ω,R2=5Ω,C1=1μF,C2=2μF, and E =6V. Calculate the charge on each capactor in the stedy state.

View Solution
