In the circuit shown below, E1=17V,E2=21V,R1=2Ω,R2=3ΩandR3=5Ω. Using Kirchhoff.s laws, find the currents flowing through the resistors R1,R2 and R3. (Internal resistance of each of the batteries is negligible.)
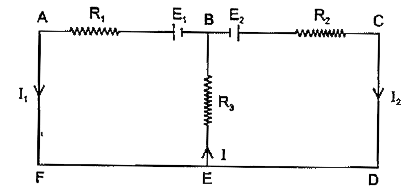
Given : E1=17V,E2=21V,R1=2Ω,R2=3Ω and R3=5Ω
In loop AFEB,
I1R1+(I1+I2)R3=E1
I1×2+(I1+I2)5=17
2I1+5I1+5I2=17
7I1+5I2=17 ........(1)
In loop BCDE,
I1R2+(I1+I2)R3=E3
I2×3+(I1+I2)5=21
5I1+8I2=21 ......(2)
On multiplying equation (1) by 5 and equation (2) by 7, we get
35I1+25I2=85
35I1+56I2=147
−−−−31I2=−62
I2=2A
7I1+5I2=17 [from equation (1)]
7I1+10=17
7I1=7
I1=1A
I=I1+I2
=1+2=3A
Similar Questions
Find the currents going through the three resistors R1,R2 and R3 in the circuit of figure.

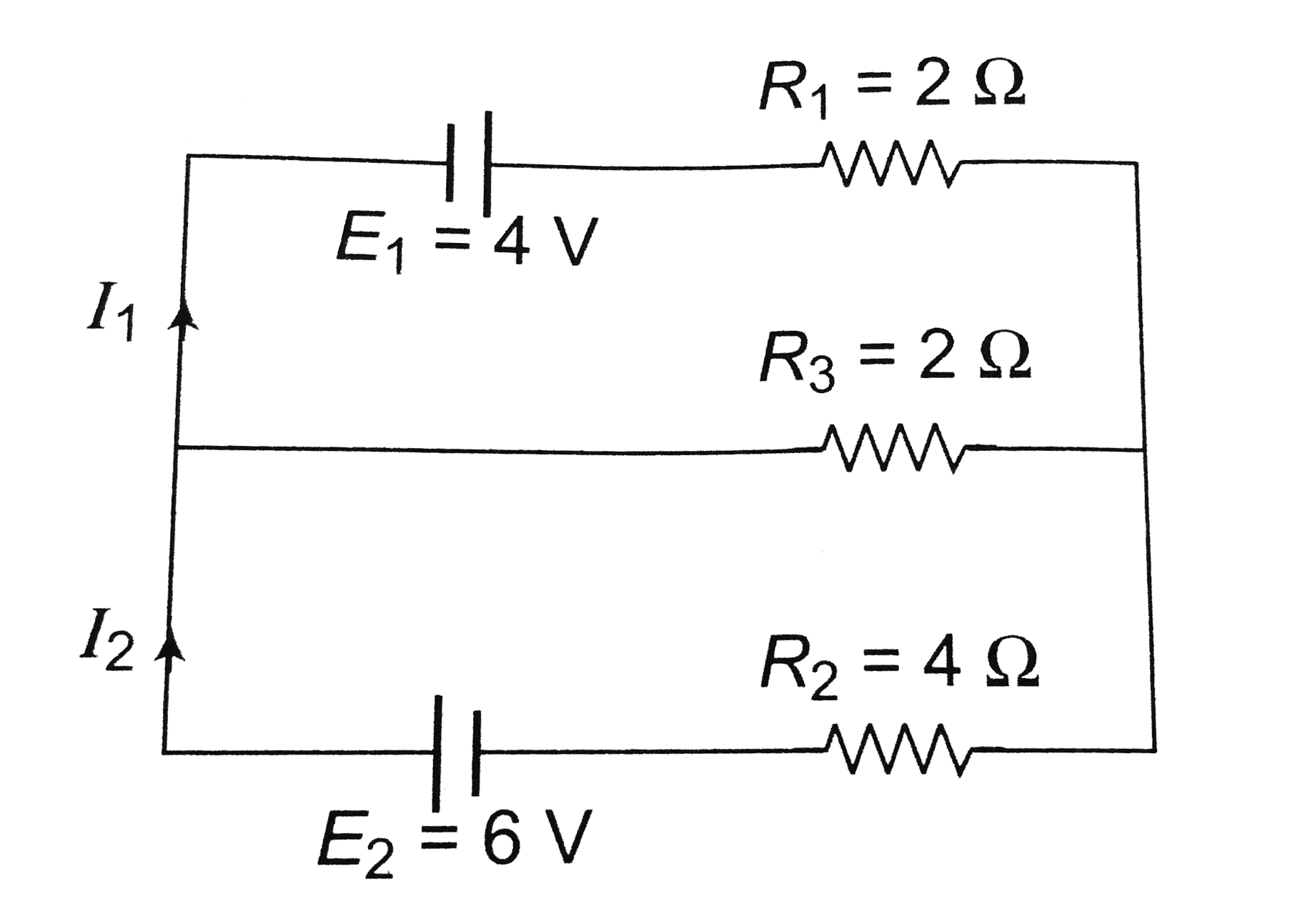
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
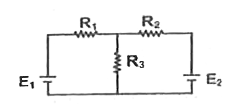
View SolutionIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3

View SolutionIn the circuit shown in figure E1=7V,E2=1V,R1=2Ω,R2=2Ω and R3=3Ω respectively. Find the power supplied by the two batteries.
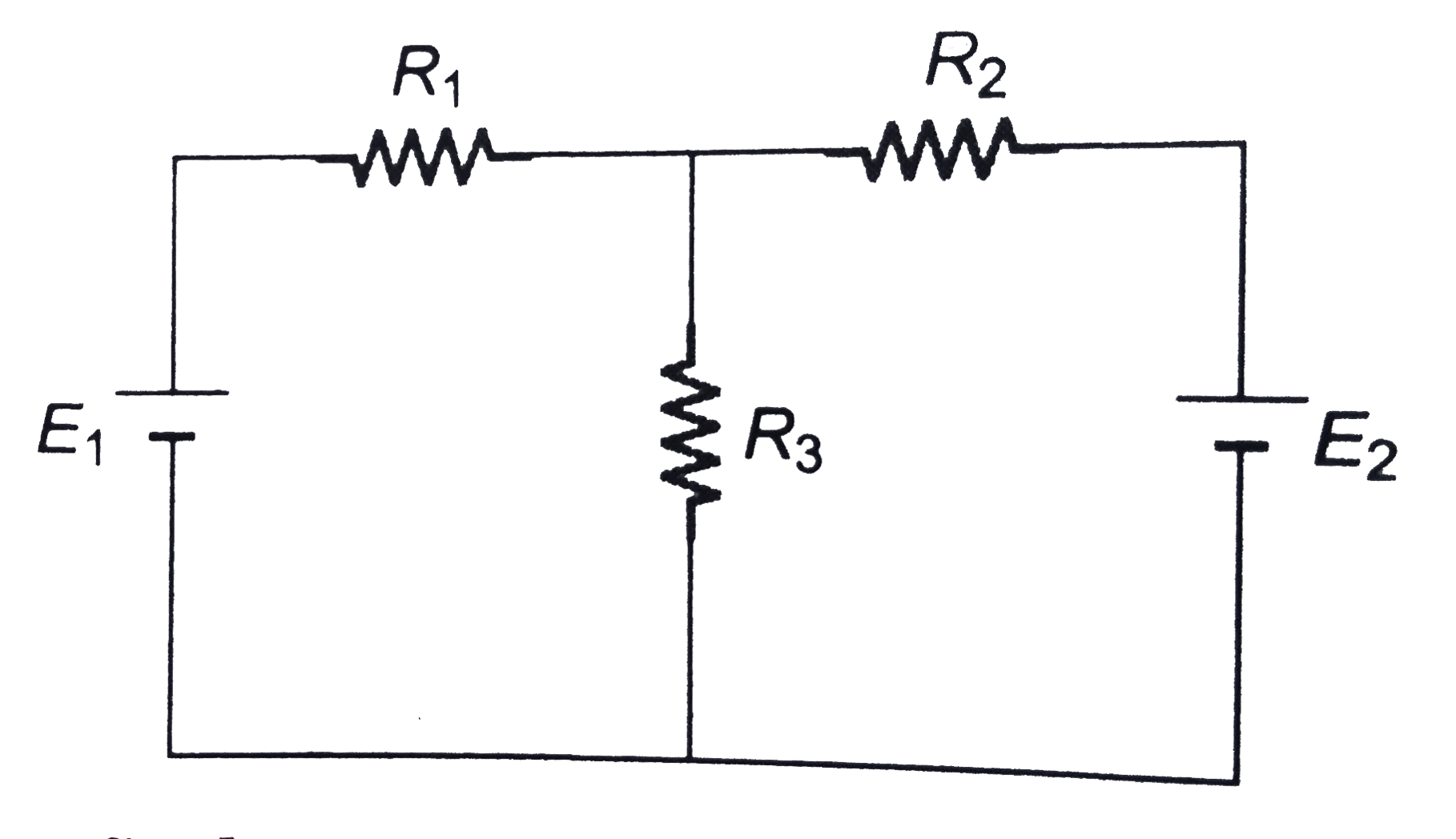
View Solution

In the circuit shown in figure. ε1=3,ε2=2,ε3=6V,R1=2,R4=6Ω,R3=2,R2=4ΩandC=5μF. Find the current in the resistor R3 and the electrical energy stored in the capacitor C.
View SolutionIn the circuit shows in Fig E=15V, R1=1Ω, R2=1Ω, R3=2Ω, and L=1.5H. The currents flowing through R1,R2,and R3 are i1,i2, and i3, respectively.

Immediately after tuning switch S on,
View SolutionIn the circuit shows in Fig E=15V, R1=1Ω, R2=1Ω, R3=2Ω, and L=1.5H. The currents flowing through R1,R2,and R3 are i1,i2, and i3, respectively.
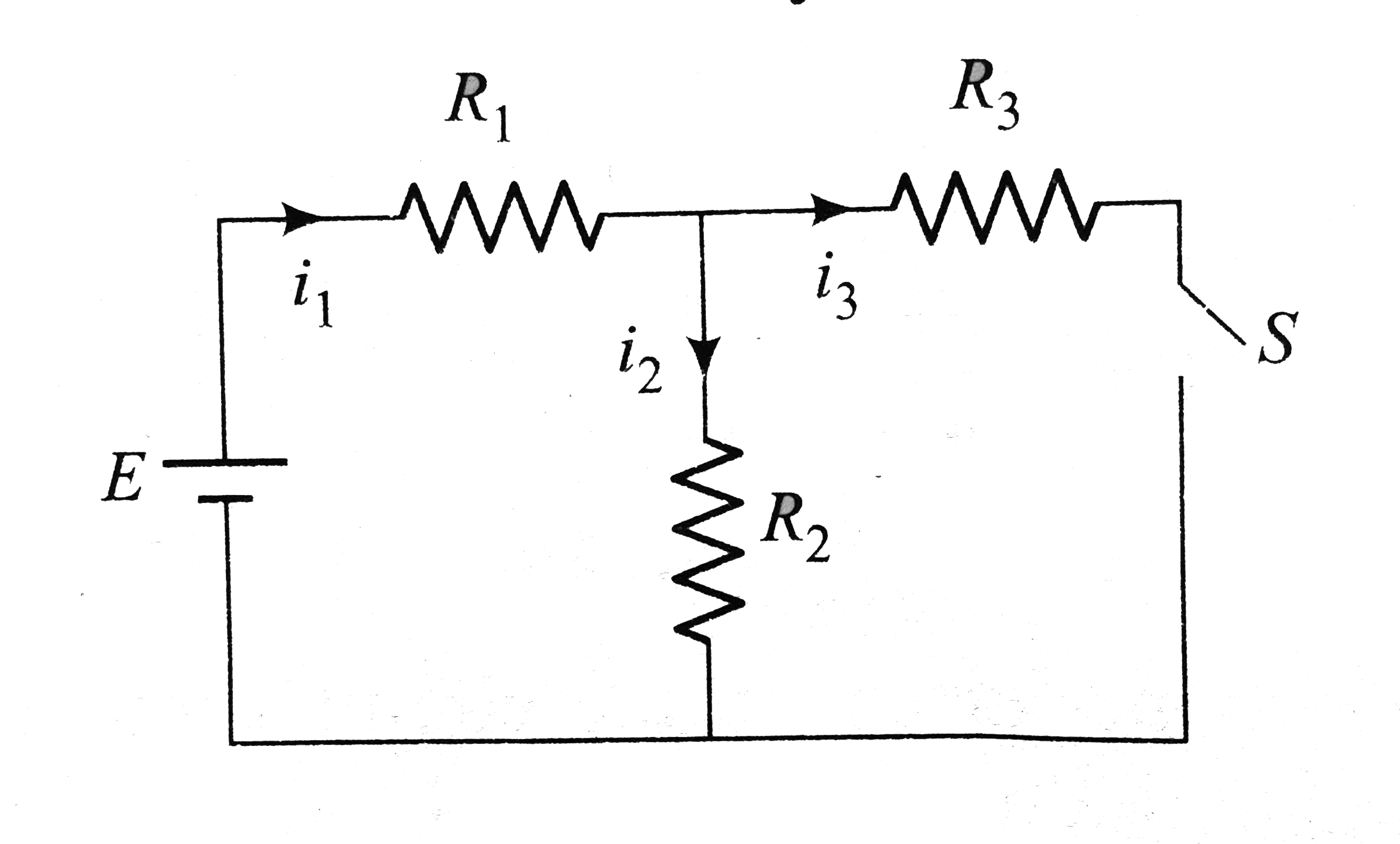
Immediately after connecting switch S,
View SolutionIn the given figure, E=12V, R1=3Ω,R2=2Ω and r=1Ω. The choose the correct option/s

View SolutionIn the following circuit ,E1=4V,R1=2Ω,
E2=6V,R2=2Ω,andR3=4Ω. Find the currents i1andi2
View Solution

