Two square metal plates of side 1m are kept 0.01m apart like a parallel plate capacitor in air in such a way that one of their edges is perpendicualr to an oil surface in the a tank filled with an insulating oil. The plates are connected to a battery of emf 500V. The plates are then lowered vertically into the oil at a speed of 0.001ms−1. Calculate the current drawn from the battery during the process.
(Dielectric constant of oil =11,ε0=8.85×10−12N−1m−2).
The correct Answer is:4.43
To solve the problem step by step, we will follow these instructions:
Step 1: Understand the Configuration
We have two square metal plates of side 1 m, separated by a distance of 0.01 m, acting as a parallel plate capacitor. The plates are connected to a battery of emf 500 V and are lowered into an insulating oil at a speed of 0.001 m/s.
Step 2: Identify Given Values
- Side of the plates, L=1m
- Separation between the plates, D=0.01m
- Dielectric constant of oil, K=11
- Emf of the battery, V=500V
- Speed of lowering plates, dxdt=0.001m/s
- Permittivity of free space, ϵ0=8.85×10−12N−1m−2
Step 3: Determine Capacitance
As the plates are lowered, part of them will be in air and part in oil. Let x be the length of the plates submerged in oil, then the length in air is L−x.
The capacitance of the part in air (denoted as C1) and the part in oil (denoted as C2) can be calculated as follows:
1. Capacitance in Air:
C1=ϵ0⋅L⋅(L−x)D
2. Capacitance in Oil:
C2=K⋅ϵ0⋅L⋅xD
Step 4: Total Capacitance
The total capacitance C is the sum of C1 and C2:
C=C1+C2=ϵ0⋅LD((L−x)+K⋅x)
C=ϵ0⋅LD(L+(K−1)x)
Step 5: Calculate Charge and Current
The charge Q on the capacitor is given by:
Q=C⋅V
The current I drawn from the battery can be expressed as:
I=dQdt=d(C⋅V)dt
Using the product rule:
I=VdCdt+CdVdt
Since V is constant, dVdt=0, so:
I=VdCdt
Step 6: Differentiate Capacitance
To find dCdt, we note that x changes with time:
dCdt=ϵ0⋅LD(K−1)dxdt
Step 7: Substitute Values
Now we substitute the known values into the equation for current:
I=V⋅ϵ0⋅LD(K−1)dxdt
Substituting the values:
I=500⋅8.85×10−12⋅10.01(11−1)⋅0.001
I=500⋅8.85×10−120.01⋅10⋅0.001
I=500⋅8.85×10−12⋅1
I=4.425×10−9A
Final Answer
The current drawn from the battery during the process is approximately:
I≈4.425nA
We have two square metal plates of side 1 m, separated by a distance of 0.01 m, acting as a parallel plate capacitor. The plates are connected to a battery of emf 500 V and are lowered into an insulating oil at a speed of 0.001 m/s.
- Side of the plates, L=1m
- Separation between the plates, D=0.01m
- Dielectric constant of oil, K=11
- Emf of the battery, V=500V
- Speed of lowering plates, dxdt=0.001m/s
- Permittivity of free space, ϵ0=8.85×10−12N−1m−2
As the plates are lowered, part of them will be in air and part in oil. Let x be the length of the plates submerged in oil, then the length in air is L−x.
C1=ϵ0⋅L⋅(L−x)D
C2=K⋅ϵ0⋅L⋅xD
The total capacitance C is the sum of C1 and C2:
C=C1+C2=ϵ0⋅LD((L−x)+K⋅x)
C=ϵ0⋅LD(L+(K−1)x)
The charge Q on the capacitor is given by:
Q=C⋅V
The current I drawn from the battery can be expressed as:
I=dQdt=d(C⋅V)dt
Using the product rule:
I=VdCdt+CdVdt
Since V is constant, dVdt=0, so:
I=VdCdt
To find dCdt, we note that x changes with time:
dCdt=ϵ0⋅LD(K−1)dxdt
Now we substitute the known values into the equation for current:
I=V⋅ϵ0⋅LD(K−1)dxdt
Substituting the values:
I=500⋅8.85×10−12⋅10.01(11−1)⋅0.001
I=500⋅8.85×10−120.01⋅10⋅0.001
I=500⋅8.85×10−12⋅1
I=4.425×10−9A
The current drawn from the battery during the process is approximately:
I≈4.425nA
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 37
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 38
1 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Advance ( Archive ) LEVEL 35
1 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
A parallel plate capacitor is charged. If the plates are pulled apart
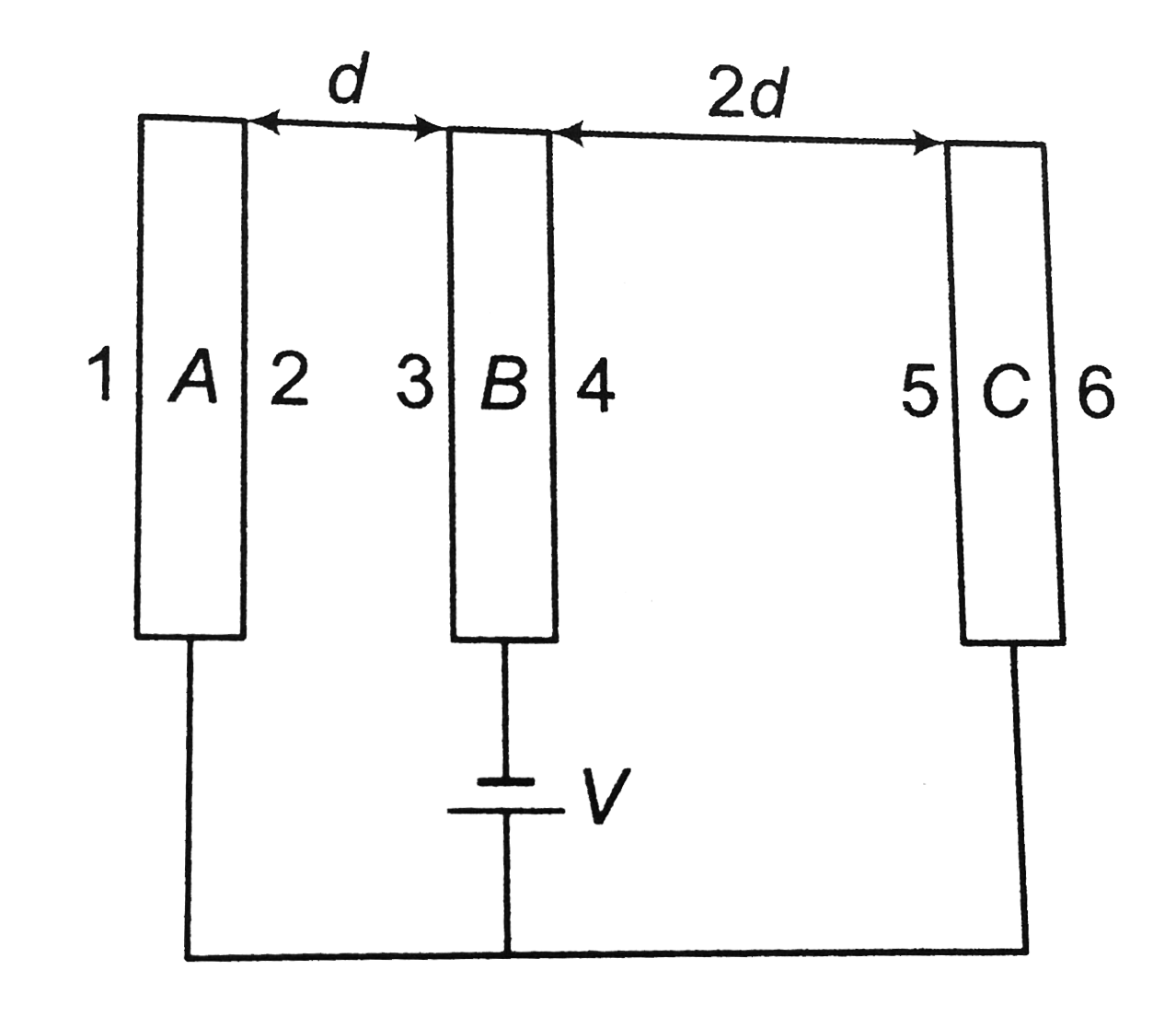
View SolutionArea of each plate is A. The conducting plates are connected to a battery of emf V volts. Find charges q1 to qt.
View SolutionThe plates of a parallel plate capacitor are not exactly parallel. The surface charge density is therefore,
View SolutionA thin metal plate P is inserted between the plates of a parallel-plate capacitor of capacitanceCin such a way that its edges touch the two plates (figure 31-Q2).The capacitance now becomes.

View SolutionA thin metal plate P is inserted between the plates of a parallel-plate capacitor of capacitance C in such a way that its edges touch the two plates (figure 31-Q2).The capacitance now becomes.

View SolutionA thin metal plate P is inserted between the plates of a parallel-plate capacitor of capacitance C in such a way that its edges touch the two plates (figure 31-Q2).The capacitance now becomes.

View SolutionA parallel plate capacitor has capacitance of 1.0F. If the plates are 1.0mm apart, what is the area of the plates?
View SolutionA parallel plate capacitor is charged and the charging battery is then disconnected. If the plates of the capacitor are moved farther apart by means of insulating handles:
View SolutionEach plate of a parallel plate capacitor has a charge q on it. The capacitor is now connected to a battery. Now,
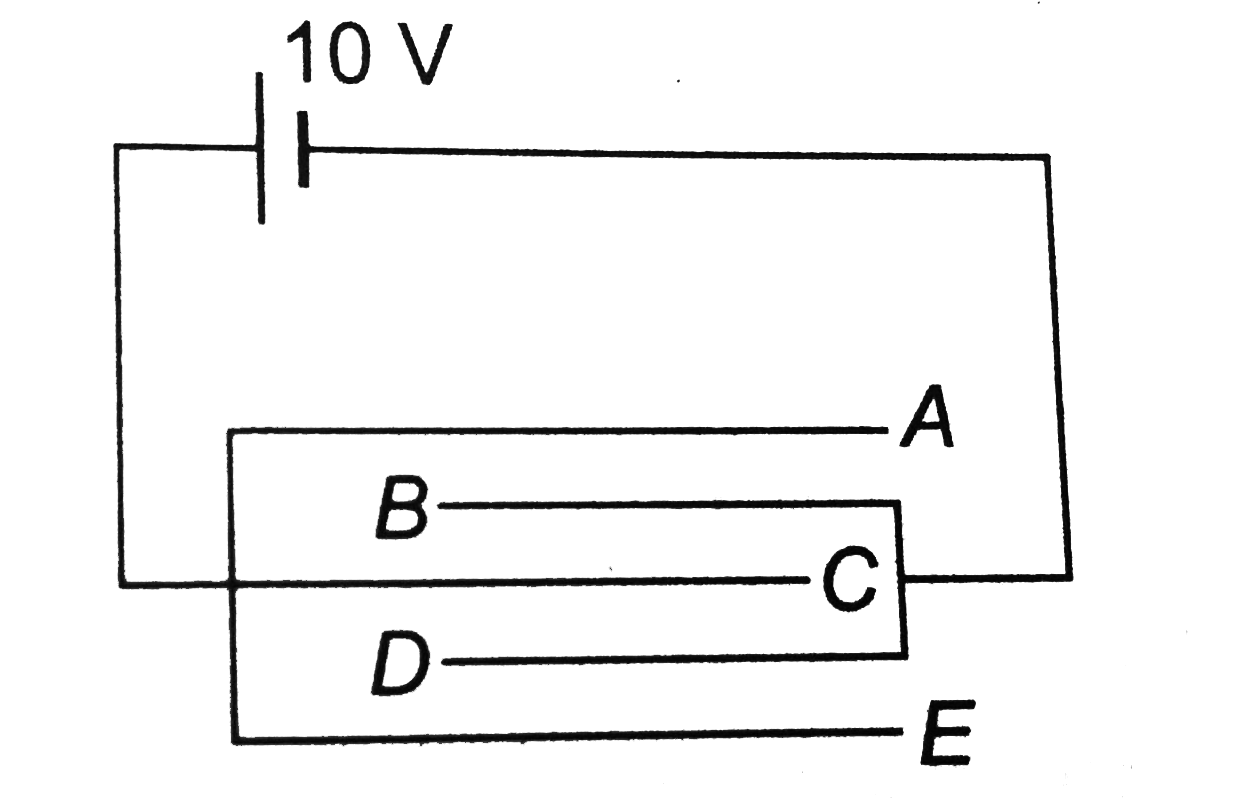
View SolutionFive identical capacitor plates are arranged such that they make four capacitors each of 2μF. The plates are connected to a source of emf 10V. The charge on plate C is
View Solution
