A 2μF capacitor that was initially uncharged is connected to a battery of EMF 100V and a resistance and the switch is closed. The heat generated in the resistance until the capacitor becomes fully charged is (in mJ):
10
20
100
200
The correct Answer is:A
To solve the problem, we need to find the heat generated in the resistance until the capacitor becomes fully charged. Here’s a step-by-step solution:
Step 1: Identify the given values
- Capacitance C=2μF=2×10−6F
- EMF of the battery V=100V
Step 2: Calculate the charge stored in the capacitor when fully charged
The charge Q stored in a capacitor is given by the formula:
Q=C×V
Substituting the values:
Q=(2×10−6F)×(100V)=200×10−6C
So, the charge Q=200μC.
Step 3: Calculate the heat generated in the resistance
The heat H generated in the resistance when the capacitor is fully charged can be calculated using the formula:
H=12CV2
Substituting the values:
H=12×(2×10−6F)×(100V)2
Calculating V2:
(100V)2=10000V2
Now substituting back:
H=12×(2×10−6)×10000
H=12×2×10−2J=10−2J
Step 4: Convert the heat from Joules to millijoules
Since 1J=1000mJ:
H=10−2J=10mJ
Final Answer
Thus, the heat generated in the resistance until the capacitor becomes fully charged is:
10mJ
---
- Capacitance C=2μF=2×10−6F
- EMF of the battery V=100V
The charge Q stored in a capacitor is given by the formula:
Q=C×V
Substituting the values:
Q=(2×10−6F)×(100V)=200×10−6C
So, the charge Q=200μC.
The heat H generated in the resistance when the capacitor is fully charged can be calculated using the formula:
H=12CV2
Substituting the values:
H=12×(2×10−6F)×(100V)2
Calculating V2:
(100V)2=10000V2
Now substituting back:
H=12×(2×10−6)×10000
H=12×2×10−2J=10−2J
Since 1J=1000mJ:
H=10−2J=10mJ
Thus, the heat generated in the resistance until the capacitor becomes fully charged is:
10mJ
Topper's Solved these Questions
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 2
40 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - JEE Main (Archive) LEVEL-1
36 Videos
- CAPACITORSBOOK - VMC MODULES ENGLISHCHAPTER - CAPACITORSEXERCISE - LEVEL 0 (LONG ANSWER TYPE)
3 Videos
- BASIC MATHEMATICS & VECTORSBOOK - VMC MODULES ENGLISHCHAPTER - BASIC MATHEMATICS & VECTORSEXERCISE - Impeccable
50 Videos
- CURRENT ELECTRICITYBOOK - VMC MODULES ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - IN-CHAPTER EXERCISE-F
10 Videos
Similar Questions
An uncharged capacitor of capacitance C is connected with a battery of EMF V and a resistance R. The switch is closed at t=0. The time instant at which the current in the circuit is V4R is t=
View SolutionThree capacitors each of capacitance C=2μF are connected with a battery of emf 30 V as shown in the figure . When the switch S is closed , the heat generated in the circuit will be
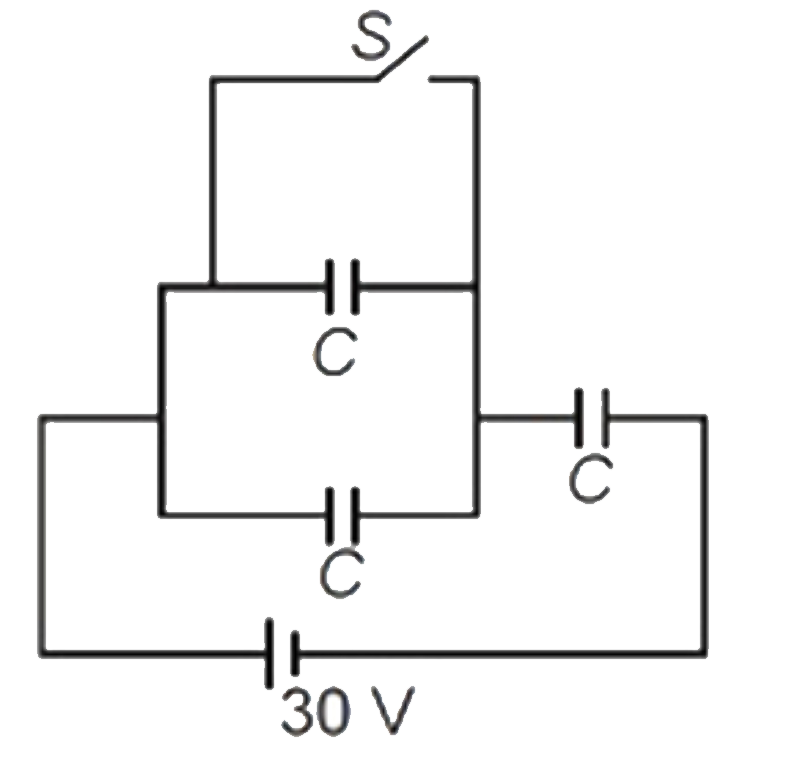
View SolutionThe area of the plates of a capacitor is 50cm2 each and the separation between them is 1mm. The space between the plates is filled with a material of dielectric constant 4. the capacitor, initially uncharged, is connected to a battery of EMF 50 V. the work done by the battery until the capacitor gets completely charged is (in μJ).
View SolutionA capacitor of capacitance C, which is initially uncharged , is connected with a battery of emf ε. Find the heat dissipated in the circuit during the process of charging .
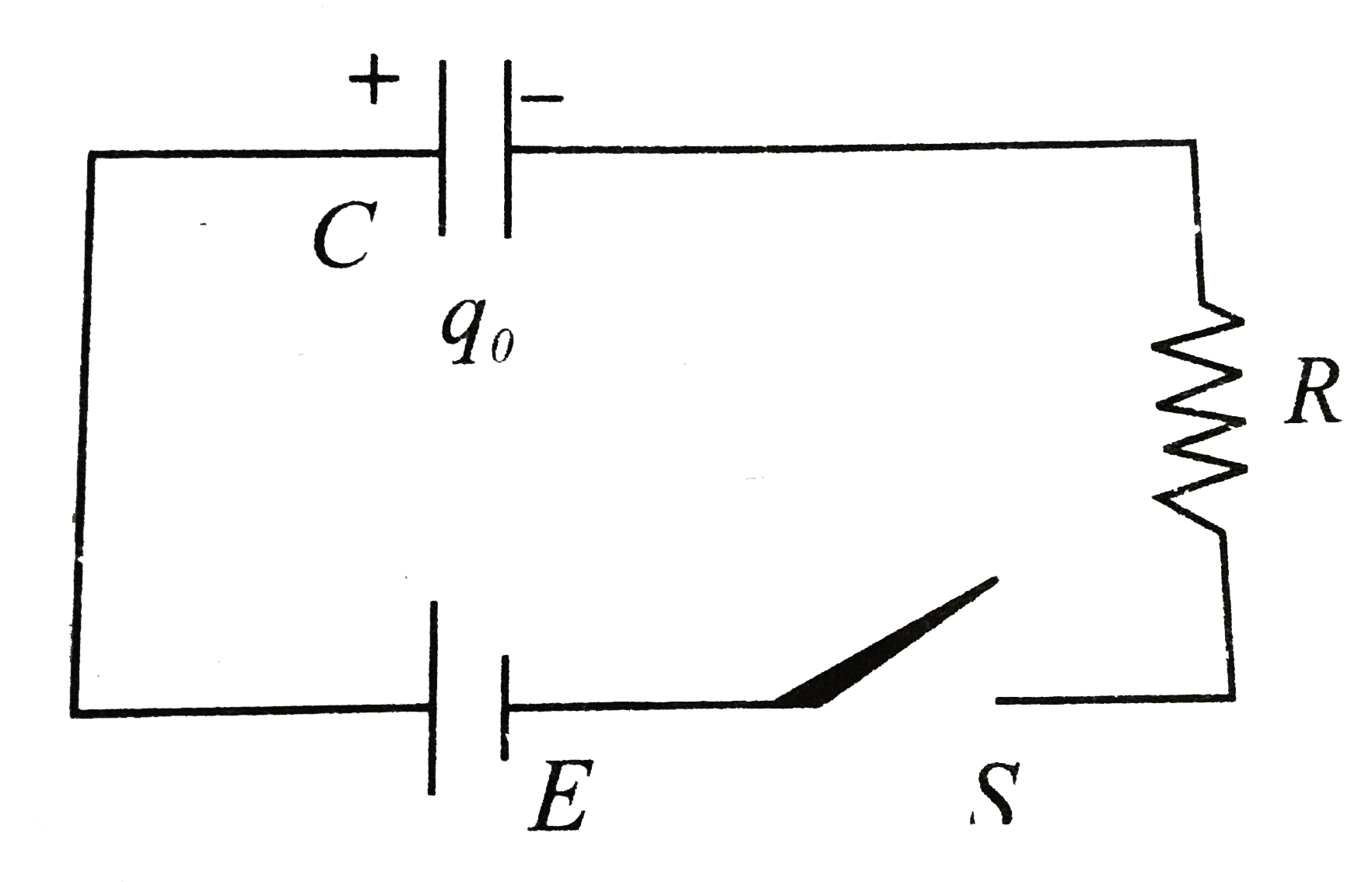
View SolutionA capacitor having initial charge q0=CE/2 is connected to a cell of emf E through a resistor R as shown. Find the total heat generated in the circuit after the switch S is closed.
View SolutionIf an uncharged capacitor is charged by connecting it with an ideal battery and a resistance R as shown. Then heat generated in resistor R by the time capacitor stores energy 18CV2 is :

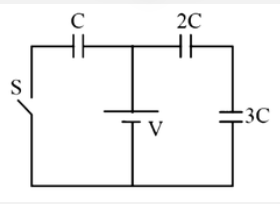
View SolutionIn the given diagram. Find the heat generated on closing the switch S (Initially the capacitor of capacitance C is uncharged ) -
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionA capacitor of capacitance C is charged to a potential difference V0 and then connected with a resistance and a battery of EMF 3V0 such that the positively charged plate of the capacitor is connected to the positive terminal of the battery. The total heat generated in the resistance until the current in the circuit becomes zero is n(CV20). the value of n is ________.
View Solution
