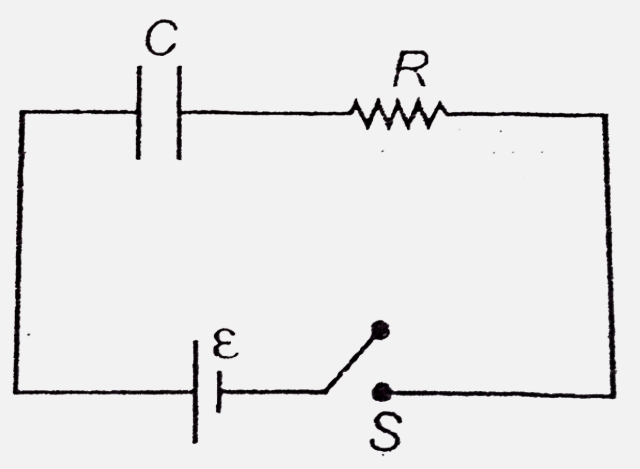
An uncharged capacitor of capacitance C is connected with a battery of EMF V and a resistance R. The switch is closed at t=0. The time instant at which the current in the circuit is V4R is t=
2RC
3RC
2RCloge2
3RCloge2
The correct Answer is:C
To solve the problem step-by-step, we will analyze the charging of a capacitor in an RC circuit and derive the time at which the current becomes V4R.
Step 1: Understand the Circuit
When the switch is closed at t=0, the capacitor starts charging through the resistor. The current in the circuit decreases over time as the capacitor charges.
Step 2: Write the Charging Equation of the Capacitor
The charge Q on the capacitor at any time t is given by the equation:
Q(t)=Q0(1−e−t/RC)
where Q0 is the maximum charge on the capacitor, R is the resistance, and C is the capacitance.
Step 3: Find the Expression for Current
The current I in the circuit is the rate of change of charge with respect to time:
I=dQdt
Differentiating the charging equation:
I=ddt(Q0(1−e−t/RC))=Q0⋅1RCe−t/RC
Substituting Q0=CV (maximum charge when fully charged):
I=CVRCe−t/RC=VRe−t/RC
Step 4: Set the Current Equal to V4R
We need to find the time t when the current I is equal to V4R:
VRe−t/RC=V4R
Canceling VR from both sides (assuming V≠0):
e−t/RC=14
Step 5: Solve for t
Taking the natural logarithm of both sides:
−t/RC=ln(14)
This can be rewritten as:
−t/RC=−ln(4)
Thus,
t=RCln(4)
Step 6: Simplify the Expression
Using the property of logarithms, we can express ln(4) as 2ln(2):
t=2RCln(2)
Final Answer
The time instant at which the current in the circuit is V4R is:
t=2RCln(2)
When the switch is closed at t=0, the capacitor starts charging through the resistor. The current in the circuit decreases over time as the capacitor charges.
The charge Q on the capacitor at any time t is given by the equation:
Q(t)=Q0(1−e−t/RC)
where Q0 is the maximum charge on the capacitor, R is the resistance, and C is the capacitance.
The current I in the circuit is the rate of change of charge with respect to time:
I=dQdt
Differentiating the charging equation:
I=ddt(Q0(1−e−t/RC))=Q0⋅1RCe−t/RC
Substituting Q0=CV (maximum charge when fully charged):
I=CVRCe−t/RC=VRe−t/RC
We need to find the time t when the current I is equal to V4R:
VRe−t/RC=V4R
Canceling VR from both sides (assuming V≠0):
e−t/RC=14
Taking the natural logarithm of both sides:
−t/RC=ln(14)
This can be rewritten as:
−t/RC=−ln(4)
Thus,
t=RCln(4)
Using the property of logarithms, we can express ln(4) as 2ln(2):
t=2RCln(2)
The time instant at which the current in the circuit is V4R is:
t=2RCln(2)
Topper's Solved these Questions
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:LEVEL 2
Explore 40 Videos
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:JEE Main (Archive) LEVEL-1
Explore 36 Videos
- CAPACITORSBook:VMC MODULES ENGLISHChapter:CAPACITORSExercise:LEVEL 0 (LONG ANSWER TYPE)
Explore 3 Videos
- BASIC MATHEMATICS & VECTORSBook:VMC MODULES ENGLISHChapter:BASIC MATHEMATICS & VECTORSExercise:Impeccable
Explore 50 Videos
- CURRENT ELECTRICITYBook:VMC MODULES ENGLISHChapter:CURRENT ELECTRICITYExercise:IN-CHAPTER EXERCISE-F
Explore 10 Videos
Similar Questions
An uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionAn uncharged capacitor of capacitance 100μF is connected to a battery of emf 20V at t = 0 through a resistance 10Ω, then
(i) the maximum rate at which energy is stored in the capacitor is :
View SolutionThree capacitors each of capacitance C=2μF are connected with a battery of emf 30 V as shown in the figure . When the switch S is closed , the heat generated in the circuit will be

View SolutionA 2μF capacitor that was initially uncharged is connected to a battery of EMF 100V and a resistance and the switch is closed. The heat generated in the resistance until the capacitor becomes fully charged is (in mJ):
View SolutionSwitch is closed at t=0 then the current in the circuit at t=L2R is
_PHY_E06_157_Q01.png)
View SolutionThree capacitors of capacitance C1=3μf,C2=6μfandC3=10μf, are connected to a 10V battery as shown in Figure 3 below
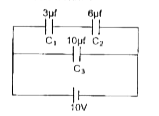
Calculate:
Equivalent capacitance
View SolutionA capacitor of capacitance C is connected to a battery of emf (ε)at t=0 through a resistance R. Find the maximum rate at which energy is stored in the capacitor. When does the rate has this maximum value?
View SolutionAt the trophic level of consumers, the rate at which food energy is assimilarted, is called ?
View SolutionAn uncharged capacitor is connected to an ideal battery through a resistance R and a switch S. Initially the switch is open . At an instant, the switch is closed . Taking this instant as t=0, which of the following graphs represent correct variation of the quantity taken along y -axis with time ?
View SolutionAn inductor L and a resistance R are connected in series with a battery of emf E and a switch. Initially the switch is open. The switch is closed at an instant t = 0. Select the correct alternatives
View Solution