A particle of mass m is initially at rest at the origin. It is subjected to a force and starts moving along the x-axis. It kinetic energy K changes with time as where is a positive constant of appropriate dimensions. Which of the following statement is (are) true?
(a)The force applied on the particle is constant
(b)The speed of the particle is proportional to time
(c)The distance of the particle from the origin increases linearly with time
(d)The force is conservative
The correct Answer is:A, B, D
(B is correct)
constnat (A is correct)
As the force is constant, its work depends only on net displacement and not on path.
So it is conservative (D is correct)
(C is incorrect)
Related Playlists
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS5videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE1videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)53videos
ENERGY & MOMENTUM
- BOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)89videos
ELECTROSTATICS
- BOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )111videos
GASEOUS STATE & THERMODYNAMICS
Similar Questions
At time t=0s particle starts moving along the x− axis. If its kinetic energy increases uniformly with time 't', the net force acting on it must be proportional to
View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA particle free to move along the (x - axis) has potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
View SolutionA particle free to move along the x−axis has potential energy given by U(x)=k[1−e−x2] for −∞≤x≤+∞, where k is a positive constant of appropriate dimensions. Then select the incorrect option
View SolutionThe velocity v of a particle of mass is moving along a straight line change with time t as d2vdt2=−Kv where K is a particle constant which of the following statement is correct?
View SolutionThe velocity v of a particle of mass m changes with time t as d2vdt=−kv, where k is constant. Now, which of the following statements is correct?
View SolutionA particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
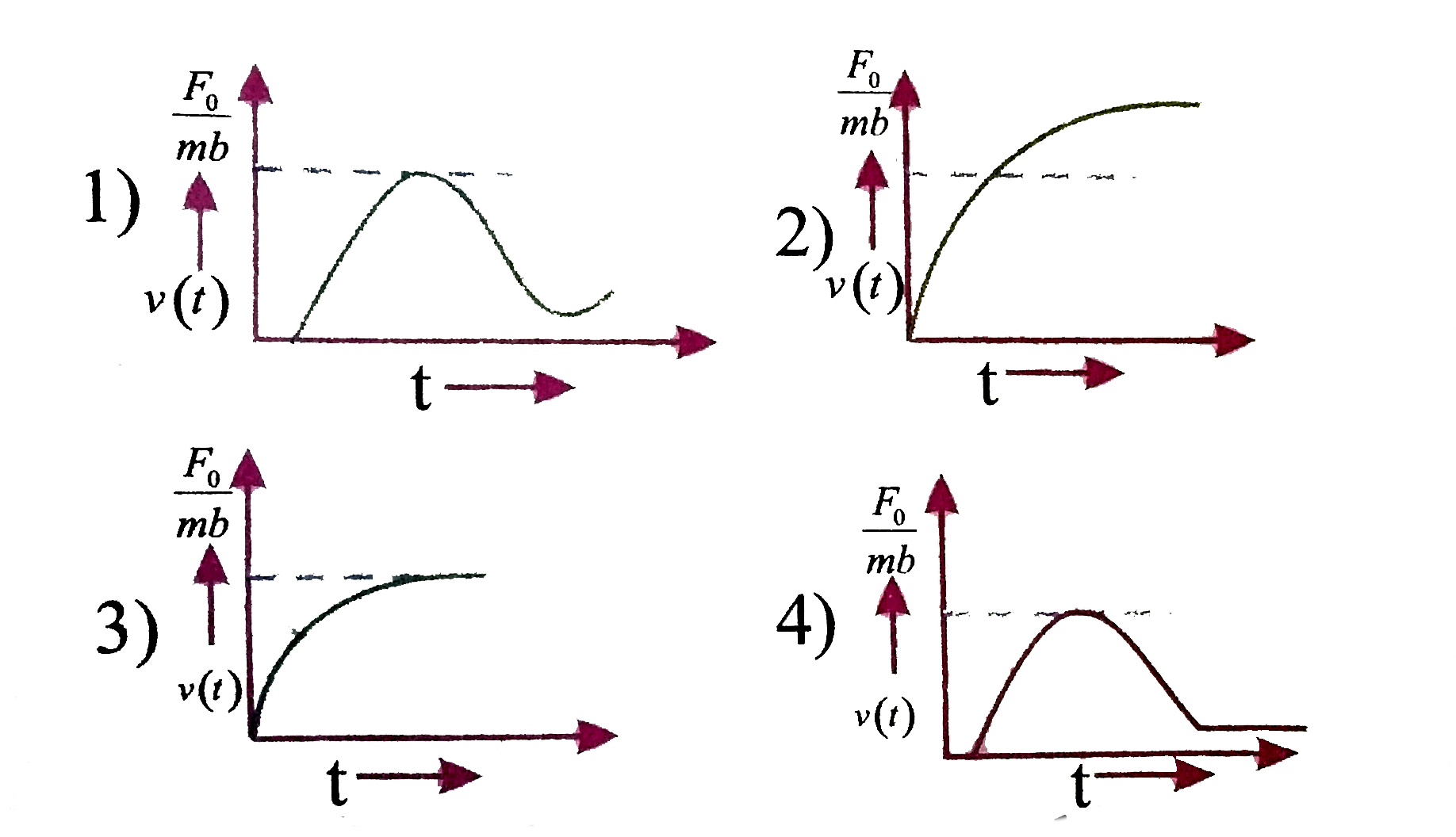 View Solution
View SolutionA particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
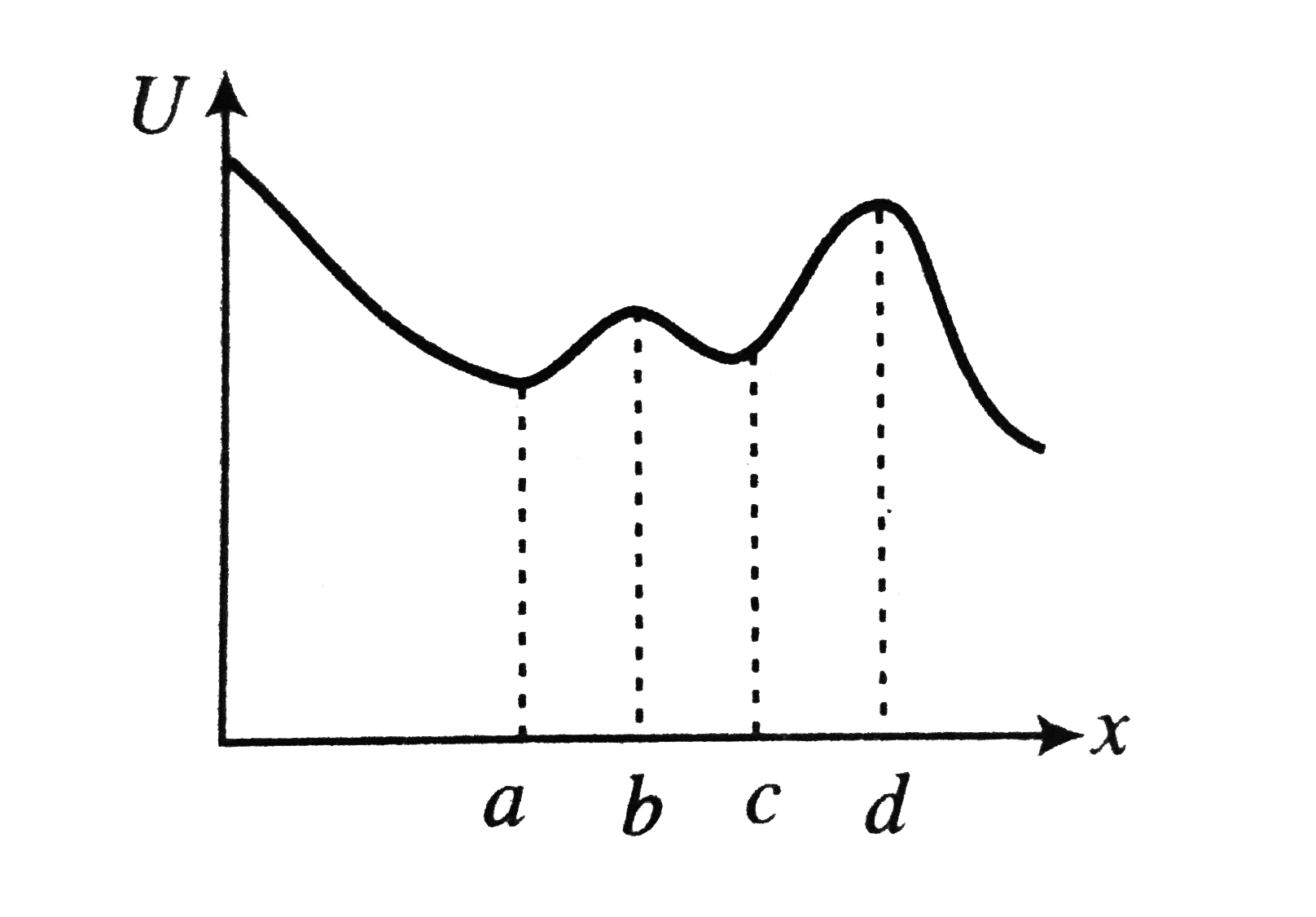 View Solution
View SolutionFigure shows a plot of the potential energy as a function of x for a particle moving along the x-axis. Which of the following statement(s) is/are true?
 View Solution
View Solution


