Particles P and Q of mass 20g and 40g respectively are simu ltaneously proejected from points A and B on the ground. The initial velocities of P and Q make 45∘ and 135∘ angles respectivley with the horizontal AB as shown in the Fig. 5.44 Each particle has an initial speed of 49m/s . the separation AB is 249m. both particles travel in the same vertical plane and undergo a collision. After collision P retraces its path. Determine the position of q when it hits the grou.d How much time after the collision does the particle Q take to reach the ground? (Take g=9.8m/s2)

The correct Answer is:3.53
The horizontal velocities of both the particle are the same and since both are projected simultaneously, these particle will meet exactly in the middle of AB (horizontally). Since
R=u2sin2θg=245m

⇒The collision takes place at the maximum height where the velocities of both the particles will be in the horizontal direction.
H=u2sin2θ2g=(49)2×sin2452×9.8=61.25m
Applying conservation of linear momentum in the horizontal direction with the information that P retraces its path, therefore its momentum will be the same in magnitude but different in direction.
Linear momentum of system before collision = Linear momentum of system after collision.
mp→vp+mQ→vQ=mp→vp+mQ→vQ
Here we have mp=20gm=m(say)andmQ=40gm=2m(say),
mux+2m−(ux)=m(−ux)+2m→vQ
Which gives →vQ=0
Since vQ=0, therefore the particle Q falls down vertically so it falls down on the mid-point of AB. Now considering vertical motion of Q
Using Sy−uyt+12ayt2
Here uy=0,sy=–61.25manday=–9.8m/s2 ⇒ −61.25=0.t−129.8t2.
Which gives t = 3.53 sec.

Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
5 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE
1 Video
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)
53 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
Two particles P & Q are projected simultaneously from a point O on a level ground in the same vertical plane with the same speed in directions making angle of 30∘ and 60∘ respectively with the horizontal.
View SolutionThree particles A, B and C are projected from the same point with the same initial speeds making angles 30∘,45∘and60∘ respectively with the horizontal. Which of the following statement is correct?
View Solution
Knowledge Check
A particle is projected at time t=0 from a point P on the ground with a speed v0, at an angle of 45∘ to the horizontal. Find the magnitude and direction of the angular momentum of the particle about P at tiem t=v0/g
Aa. mv302√2gBb. mv30√2gCc. 3mv30√2gDd. √2mv30g
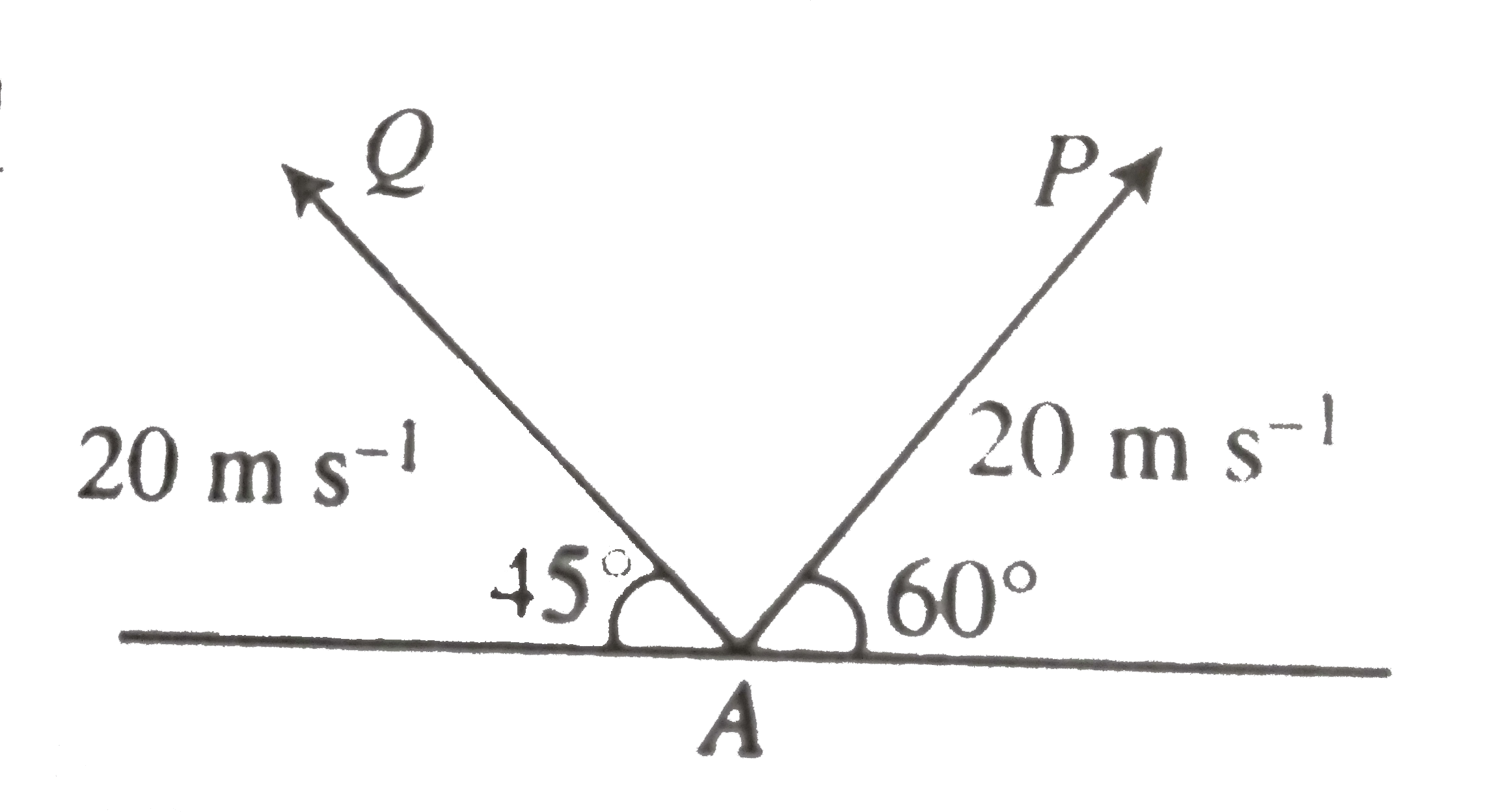
Two particles P and Q are projected simultaneously away from each other from a point A as shown in figure. The velocity of P relative to Q in ms−1 at the instant when the motion of P is horizontal is
View SolutionA particle is projected with velocity 50 m/s at an angle 60∘ with the horizontal from the ground. The time after which its velocity will make an angle 45∘ with the horizontal is
View SolutionTwo particles P and Q are projected from two points in the same plane as shown. Find the condition for collision of two paricles.
View SolutionTwo particles are simultaneously thrown in horizontal direction from two points on a riverbank, which are at certain height above the water surface. The initial velocities of the particles are v1=5m/sandv2=7.5m/s respectively. Both particles fall into the water at the same time. First particles enters the water at a point s = 10 m from the bank. Determine
(a) the time of flight of the two particles,
(b) the height from which they are thrown,
(c) the point where the second particle falls in water.
View SolutionA particle is projected from horizontal making an angle of 53∘ with initial velocity 100ms−1. The time taken by the particle to make angle 45∘ from horizontal is
View SolutionTwo particles A and V are projected in the vertical plane with same initial velocity u0 from part (0,0) and (l,-h) towards each other as shown in figure
The path of particle A with respect to particle B will be –

View SolutionThe particle of mass 1 kg is projected with velocity 20√2m/s at 45∘ with ground . When , the particle is at highest point (g=10m/s2),
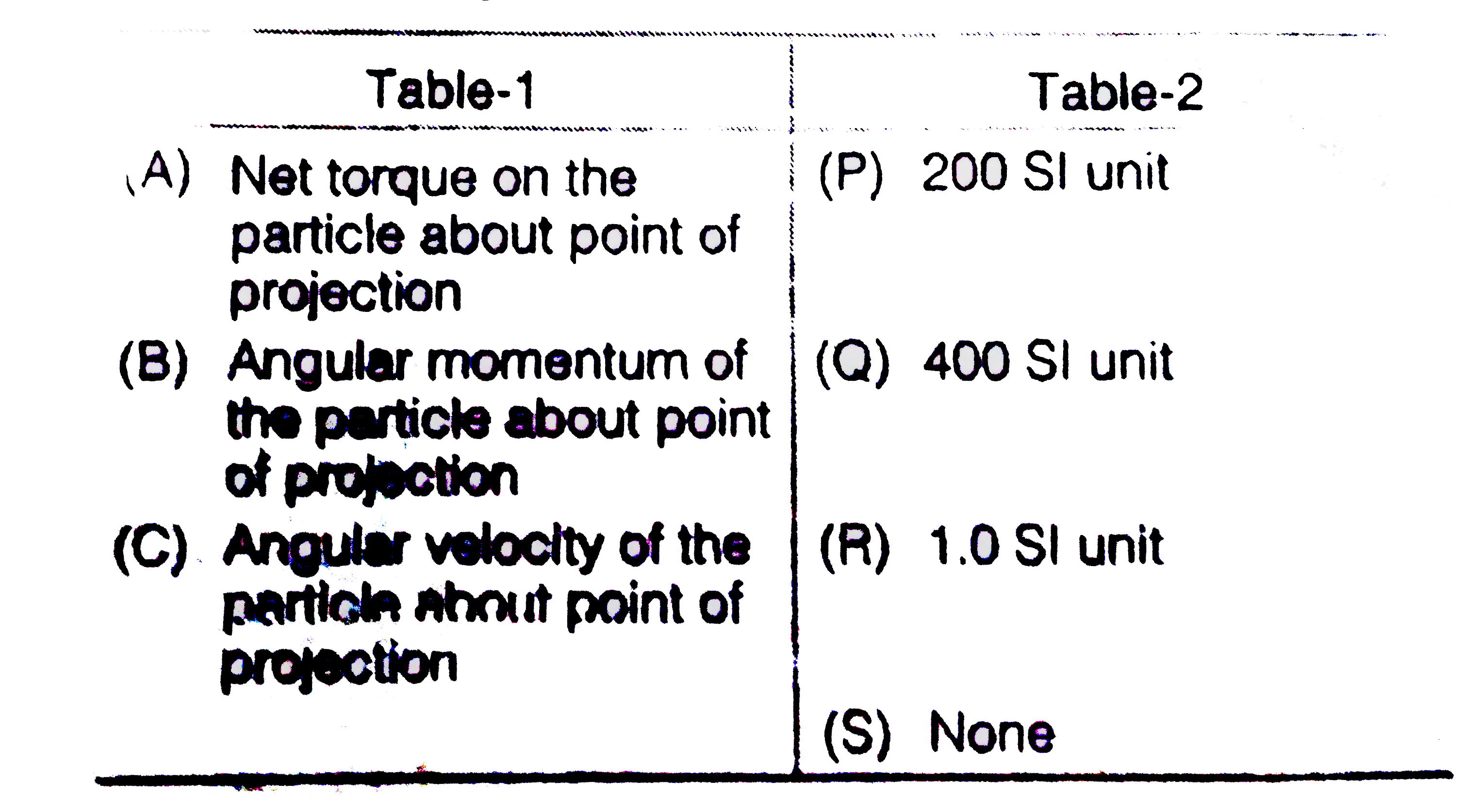
View Solution
