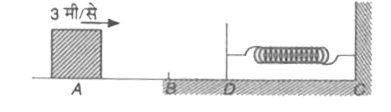
A 0.5kg block slides from the point A on a horizontal track with an initial speed 3m/s towards a weightless horizontal spring of length 1m and force constant 2N/m. The part AB of the track is frictionless and the part BC has the coefficient of static and kinetic friction as '0.22' and 0.20 respectively. If the distances AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
The correct Answer is:4.24
The block strikes the spring and compresses it by the distance x.
Using work energy theorem
Wtotal=ΔK⇒Wfriction+Wspring=Kfinal−Kinitial
(0−12mv2)=−μkmg(2.14+x)−12kx2
12×0.5×32=0.2×0.5×9.8(2.14+x)+122×x2
2.14+x+x2=2.25 ∴ x2+x−0.11=0
On solving we get x=−1110orx=110=0.1m
Here the body stops momentarily.
Restoring force at this position
Fs=kx=2×0.1=0.2N
Frictional force at this position
Flim=μsmg=0.22×0.5×9.8=1.078N
Since frictional force > Restoring force the body will stop here. The total distance travelled
= AB + BD + DY = 2 + 2.14 + 0.1 = 4.24 m.

Topper's Solved these Questions
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
Explore 5 Videos
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE
Explore 1 Video
- ENERGY & MOMENTUMBook:VMC MODULES ENGLISHChapter:ENERGY & MOMENTUMExercise:JEE MAIN (ARCHIVE)
Explore 53 Videos
- ELECTROSTATICSBook:VMC MODULES ENGLISHChapter:ELECTROSTATICSExercise:JEE Advanced (Archive)
Explore 89 Videos
- GASEOUS STATE & THERMODYNAMICSBook:VMC MODULES ENGLISHChapter:GASEOUS STATE & THERMODYNAMICSExercise:JEE ADVANCED (ARCHIVE )
Explore 111 Videos
Similar Questions
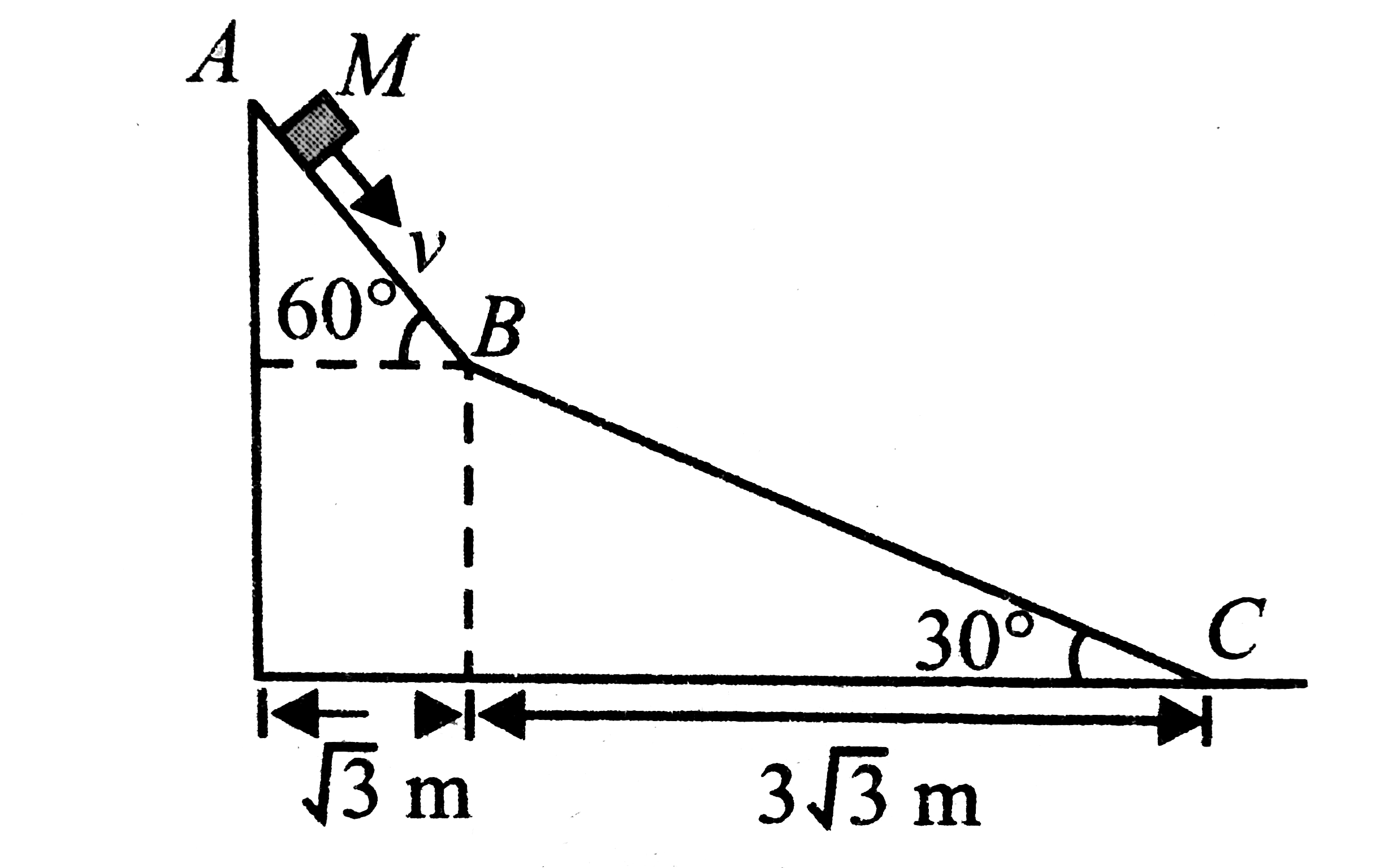
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
View SolutionThese questions consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following five reponses
(a) If both Assertion and Reason arecorrect and Reason is the correct explanation of Asserrtion.
(b) If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
(c ) If Assertion is true but Reason is false.
(d) If Assertion is false but Reason is true.
Assertion A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving through a certain distance.
The surface is now tilted to an angle of 30∘ with the horizontal and the same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is smaller than that in the first situation.
Reason The coefficient of friction between the block and the surface decreases with the increase in the anglle of inclination.
View SolutionA spring of force constant 800 N/m has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is:
View SolutionA hollow metal sphere of radius 5 cm is charged so that the potential on its surface is 10 V. The potential at the centre of the sphere is
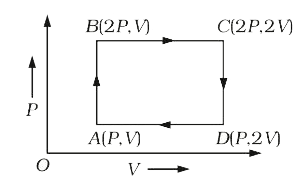
View SolutionAn ideal gas is taken around the cycle ABCDA as shown in the P-V diagram. What is the work done during the cycle?
View SolutionA 0.5 kg block sides from the point A (see fig) on a hurizontal track as wil initial speed of 3 m//s toward a weightes horizental spring of length 1 in and force constant 2 newtav in the part AB of the track is frictionless friction and the per BC has the coefficient of the state AB and and BDare 2 m and 2.14 m repectively , find the total distance through which the block move before if conseto rest completely (Taking=10m/s2) .
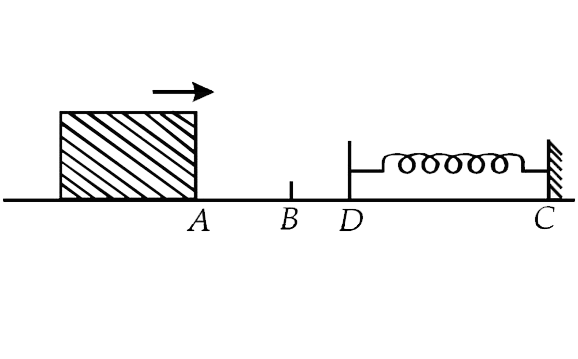
View SolutionA 0.5kg block slides from the point A on a horizontal track with an initial speed 3 m//s towards a weightless horizontal spring of length 1m and force constant 2N//m. The part AB of the track is frictionless and the part BC has the confficient of static and kinetic friction as 0.20 respectively. If the distancences AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
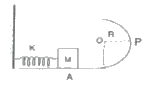
View SolutionFigure shows a smooth track, a part of which is a circle of radius r. A block of mass m is pushed against a spring of spring constant k fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal.
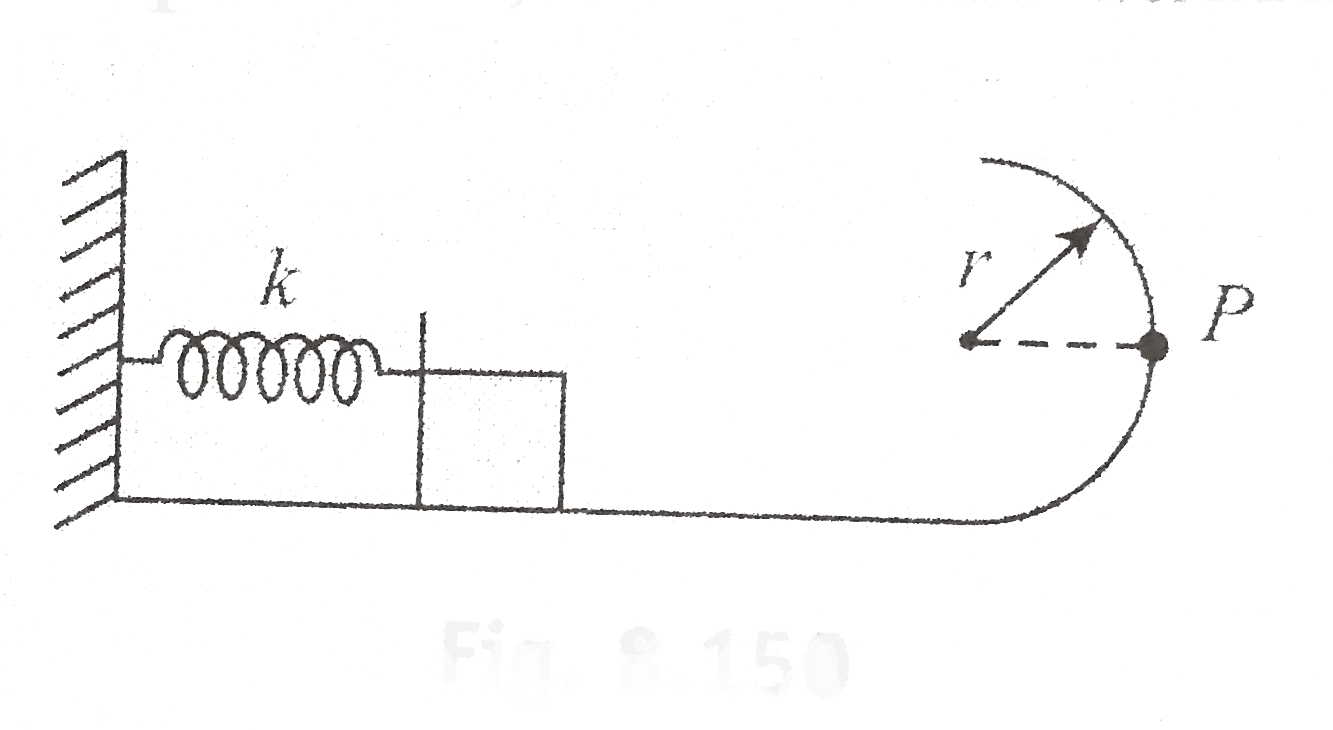
View Solution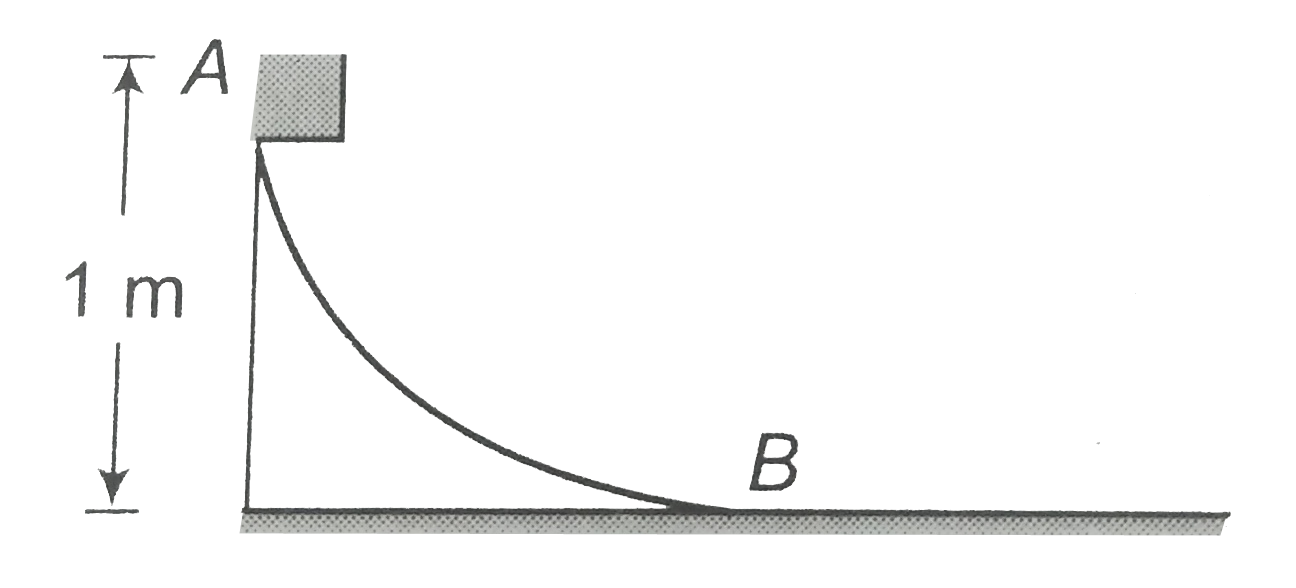
A block weighing 10 kg travels down a smooth curved track AB joined to a rough horizontal surface (see the figure.) The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1 m above the horizontal surface, how far will it move on the rough surface?
View SolutionA block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block is released from rest on the track from a point 1.0 m above the horizontal surface, the distance it will move on the rough surface is
View Solution0.5 किग्रा द्रव्यमान का एक ब्लॉक के एक क्षैतिज मार्ग बिंदु A से 3 मी/से की प्रारंभिक चाल से 1 मी लम्बाई तथा 20 न्यूटन/मी बल नियतांक वाले भारहीन स्प्रिंग की और गतातिमान है। क्षैतिज मार्ग का भाग AB घर्षणहीन है तथा भाग BC में गतिज तथा स्थैतिज घर्षण गुणांक क्रमश 0.2 तथा 0.22 है। यदि AB तथा BD भागो की लम्बाईयाँ क्रमशः 2 मी तथा 2.14मी है तो विरामावस्था में आने से पहले ब्लॉक द्वारा चली कुल दुरी ज्ञात कीजिए। (g=10ms2)
View SolutionA 0.5 kg block slides from a point A [fig.1.17] on a horizontal track with an initial speed of 3m.s−1 towards a weightless horizontal spring of length 1 m and of force constant 2N.m−1. The part AB of the track is frictionless and the part BC has coefficients of static and kinetic friction as 0.22 and 0.2 respectively. If the distance AB and BD are 2 m and 2.14 m respectively. Find the total distance covered by the black before it comes to rest (g=10m.s−2)
View SolutionThe figure shows a smooth track, a part of which is a circle of radiur R. A block ofmas m is pushed against a spring of spring constant K fixed at the left end and is then released. Find the initial compression of the spring so that the block presses the track with a force mg when it reaches the point P, where the radius of the track is horizontal?
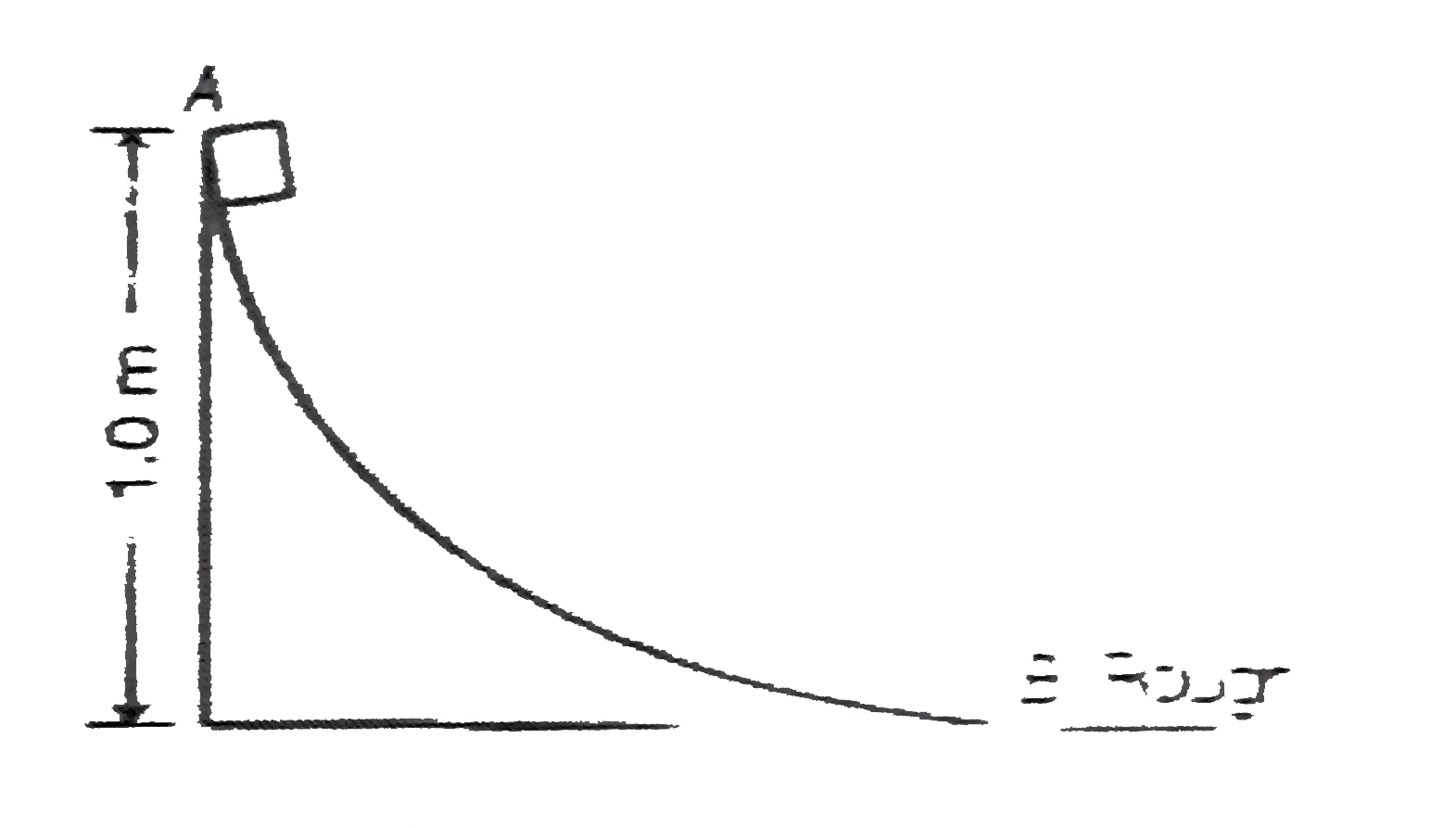
View SolutionA block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block starts slipping on the track from a point 1.0 , above the horizontal surface, the distance it will move on the rough surface is x meter. Then value of x.

View SolutionA 0.5kg block slides from the point A on a horizontal track with an initial speed 3 m//s towards a weightless horizontal spring of length 1m and force constant 2N//m. The part AB of the track is frictionless and the part BC has the confficient of static and kinetic friction as 0.20 respectively. If the distancences AB and BD are 2m and 2.14m respectively, find total distance through which the block moves before it comes to rest completely. (g=10 m//s^(2) ).
View SolutionA block weighing 10 N travels down a smooth curved track AB joined to a rough horizontal surface (figure). The rough surface has a friction coefficient of 0.20 with the block. If the block is released from rest on the track from a point 1.0 m above the horizontal surface, the distance it will move on the rough surface is
View Solution