A sphercial ball of mass m is kept at the highest point in the space between two fixed, concentric spheres A and B (figure). The small sphere A has a radius R, and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. The ball is given a gentle push (towards the right figure). The angle made by the radius vector of the ball with the upward vertical is denoted by θ (shown in figure).

a. Express the total normal reaction force exerted by the sphere on the ball as a function of angle θ.
b. Let NA and NB denote the magnitudes of the normal reaction forces on the ball exerted by spheres A and B, respectively. Sketch the variations of NA and NB as functions of cosθ in the range 0≤θ≤π by drawing two separate graphs in your answer book, taking cosθ on the horizontal axes.
The correct Answer is:0,2
The ball is moving in a circular motion. The necessary centripetal force is provided by (mgcosθ−N).
Therefore mgcosθ−NA=mv2(R+d/2)p …..(i)
According to mechanical energy conservation
ΔK+ΔU=0
(12mv2−0)+(−mgh)=0
12mv2=mg(R+d2)(1−cosθ) ....(iii)
From (i) and (ii)
NA=mg(3cosθ−2) .....(iii)

The above equation shows that as θ increases NA decreases. At a particular value of θ . NA will become zero and the ball will lose contact with sphere A. This condition can be found by putting NA = 0 in eq. (III) 0=mg(3cosθ−2)
∴θ=cos−1(23)
The graph between NAandcosθ
From eq. (iii) when θ=0,NA=mg .
When θ=cos−1(23),NA=0
The graph is a straight line as shown.
When θ=cos−1(23)
NB+mgcosθ=mv2(R+d2)

12mυ2=mg(R+d2)(1−cosθ)
mυ2(R+d2)=2mg(1−cosθ) .....(v)
From (iv) and (v) we get
NB+mgcosθ=2mg−2mgcosθ,NB=mg(2−3cosθ)
When cosθ=23,NB=0
When cosθ=−1,NB=5mg. Therefore the graph is as shown.

Topper's Solved these Questions
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - PARAGRAPH QUESTIONS
5 Videos
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE ADVANCE (ARCHIVE) - ASSERTION & REASON TYPE
1 Video
- ENERGY & MOMENTUMBOOK - VMC MODULES ENGLISHCHAPTER - ENERGY & MOMENTUMEXERCISE - JEE MAIN (ARCHIVE)
53 Videos
- ELECTROSTATICSBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - JEE Advanced (Archive)
89 Videos
- GASEOUS STATE & THERMODYNAMICSBOOK - VMC MODULES ENGLISHCHAPTER - GASEOUS STATE & THERMODYNAMICSEXERCISE - JEE ADVANCED (ARCHIVE )
111 Videos
Similar Questions
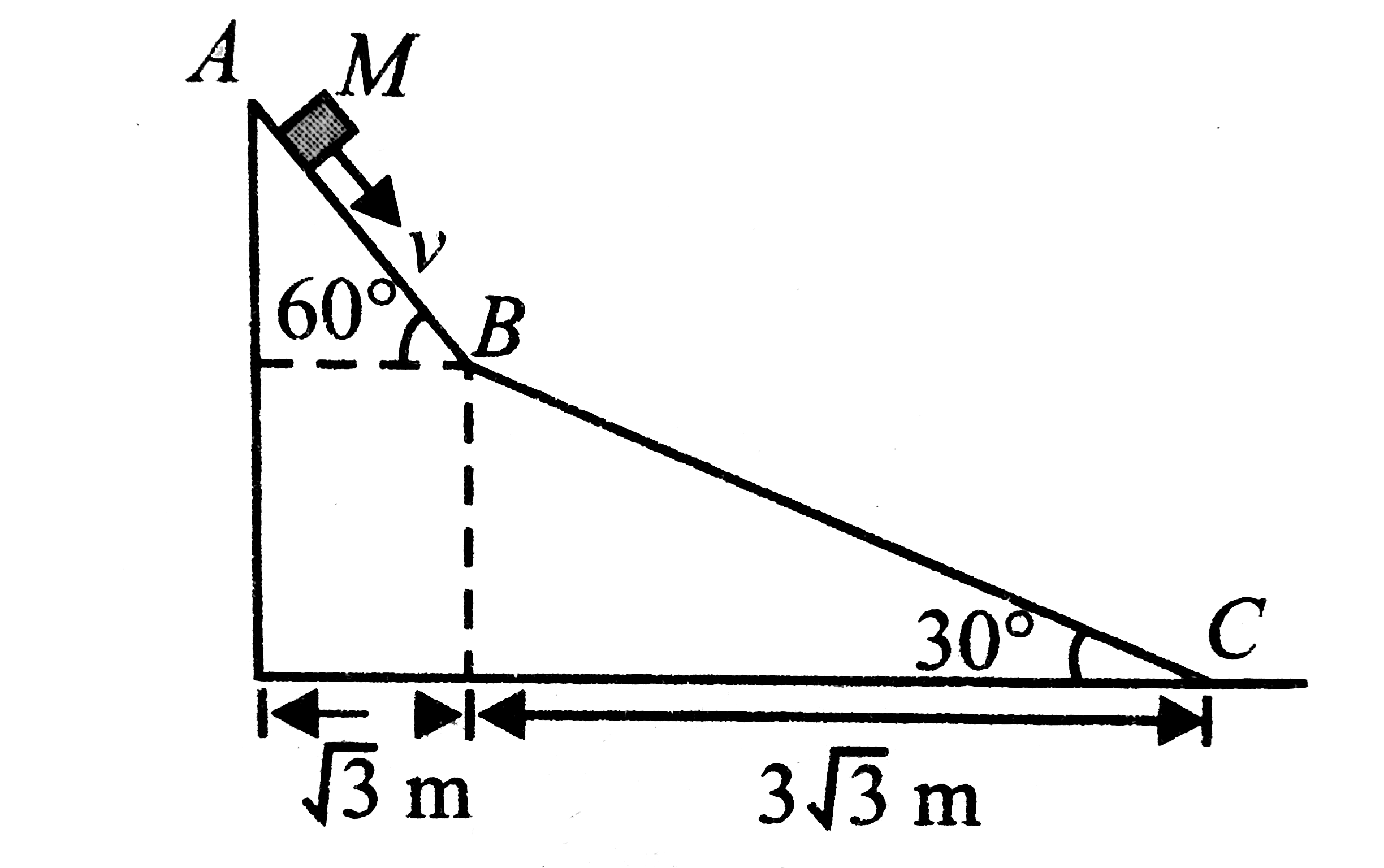
A small block of mass M moves on a frictionless surface of an inclined plane, as shown in the figure. The angle of the incline suddenly changes from 60∘ to 30∘ at point B. The block is many at rest at A. Assume that collisions between the block id the incline are totally inelastic.
The speed of the block at point C, immediately before it leaves the second incline
View SolutionThese questions consists of two statements each printed as Assertion and Reason. While answering these question you are required to choose any one of the following five reponses
(a) If both Assertion and Reason arecorrect and Reason is the correct explanation of Asserrtion.
(b) If both Assertion and Reason are correct but Reason is not the correct explanation of Assertion.
(c ) If Assertion is true but Reason is false.
(d) If Assertion is false but Reason is true.
Assertion A block of mass m starts moving on a rough horizontal surface with a velocity v. It stops due to friction between the block and the surface after moving through a certain distance.
The surface is now tilted to an angle of 30∘ with the horizontal and the same block is made to go up on the surface with the same initial velocity v. The decrease in the mechanical energy in the second situation is smaller than that in the first situation.
Reason The coefficient of friction between the block and the surface decreases with the increase in the anglle of inclination.
View SolutionA spring of force constant 800 N/m has an extension of 5 cm. The work done in extending it from 5 cm to 15 cm is:
View SolutionA hollow metal sphere of radius 5 cm is charged so that the potential on its surface is 10 V. The potential at the centre of the sphere is
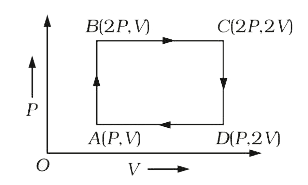
View SolutionAn ideal gas is taken around the cycle ABCDA as shown in the P-V diagram. What is the work done during the cycle?
View SolutionA spherical balll of mass m is the highest point in the space between two fixed , concentic sphere A and B the smaller the two sphere A has a radius R and the space between the two spheres has a width d . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by θ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle θ
(b) Let N_(A)andNBdenote in the magnitubes of the normal reaction force on the bell evered by the sphare A and B repectively Skech the variation of NAandN_(B)asfunctionsofcos theta ∈theran≥0 le theta le pi bydraw∈gtwoseparategraph∈youranswerb∞ktak∈gcos theta an the horizental axas.
View SolutionA small spherical ball of mass m is projected from lowest point (point P) in the space between two fixed, concentric spheres A and B (see figure). The smaller sphere A has a radius R and the space between the two spheres has a width d. The ball has a diameter very slightly less than d. All surfaces are frictionless. Speed of ball at lowest point is v. NA and NB represent magnitudes of the normal reaction force on the ball exerted by the spheres A and B respectively. Match the value of v given in column–I with corresponding results in column–II.

View SolutionA small ball (of negligible size) is placed over a sphere of same mass and radius 1 m as shown. All surface are smooth. A slight push is given to the ball. When the radius vector joining the ball makes an angle of 30∘ with the vertical, speed of sphere is v.(g=10m/s2)
If mass of ball and sphere be 1 kg each then the normal reaction between the two at this instant is ltBRgt
View SolutionA friction wire AB is fixed on a sphere of radius R. A very small spherical ball slips on this wire. The time taken by the ball to slip from A to B.

View Solutionद्रव्यमान m की एक गोलाकार गेंद दो स्थिर, सकेंद्रित गोलों A तथा B के बीच के स्थान में उच्चतम बिंदु पर रखी गई है। छोटे गोले A की त्रिज्या R है, तथा दोनों गोलों के बीच के स्थान के चौड़ाई d है गेंद का व्यास, d से थोड़ा कम है। सभी तल घर्षणहीन है। गेंद को एक हल्का-सा धक्का दे और दिया जाता है। गेंद का त्रिज्य वेक्टर, उर्ध्वार्धर से θ कोण बनाता है
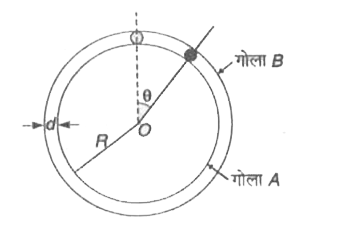
(a) गोलों द्वारा गेंद पर आरोपित अभिलम्ब प्रतिक्रिया बल, कोण θ के फलन के रूप में व्यक्त कीजिए।
(b) माना गोलों A तथा B द्वारा गेंद पर आरोपित अभिलम्ब प्रतिक्रिया के परिमाण क्रमशः NA तथा NB है। NA तथा NB के विचारणो को 0≤θ≤π परास में, cosθ के फलन के रूप में (cosθ क्षैतिज अक्ष के अनुदिश दो अलग-अलग लेखाचित्रो द्वारा दिखाइए।
View SolutionA spherical balll of mass m is the highest point in the space between two fixed , concentic sphere A and B the smaller the two sphere A has a radius R and the space between the two spheres has a width d . The bell has a disneter very dightly less then d . All surface are frictionless . The bell is a given a gentle push (owards the right in the figure ) The upward vertical is denoted by θ (shown ijn the figure)

(a)Express the total normal reaction force exerted by the sphore on the as a finction of angle θ
(b) Let N_(A)andNBdenote in the magnitubes of the normal reaction force on the bell evered by the sphare A and B repectively Skech the variation of NAandN_(B)asfunctionsofcos theta ∈theran≥0 le theta le pi bydraw∈gtwoseparategraph∈youranswerb∞ktak∈gcos theta an the horizental axas.
View SolutionThe radii of two spheres of mass M and 5M are R and 2R respectively. The two centers were left in space at a distance of 12R. If they only attract each other by the gravitational ball, the small sphere will pass through before colliding.
View Solution5 cm और 60 cm व्यासार्थ के दो संकेन्द्री गोलों वाले गोलाकार संधारित्र कि धारिता निकालें । दोनों गोलों के बीच वाले स्थान में भरे हुए पदार्थ का परावैधुतांक 6 है।
View SolutionR त्रिज्या के एक गोले में A तथा B के बीच घर्षण रहित तार लगा है। एक बहुत छोटी गोलाकार गेंद इस तार पर फिसलती है। गेंद का A से B तक फिसलने में लगा समय होगा

View Solutionएक छोटे चालक गोले (त्रिज्या r) को त्रिज्या R के एक बड़े चालक खोखले गोले में संकेन्द्रीय स्थिति में रखा गया है | बड़े तथा छोटे गोलों को क्रमशः Q और q (Q>q) से आवेशित करके परस्पर पृथक्कृत रखा जाता है | गोलों के मध्य विभवान्तर होगा
View SolutionA spherical ball of mas m is kept at the highest point in the space between two fixed, concentric spheres A and B as shown in figure. The sphere A has radius R and sphere B has radius R+d. All surfaces are smooth. The diameter of ball slightly less than d. The ball is given a gentle push so that angle made by radius vector of the ball with vertical is θ. NA and NB are the magnitudes of normal reaction forces on the ball exerted by spheres A and B respectively. The match the following

View Solution
