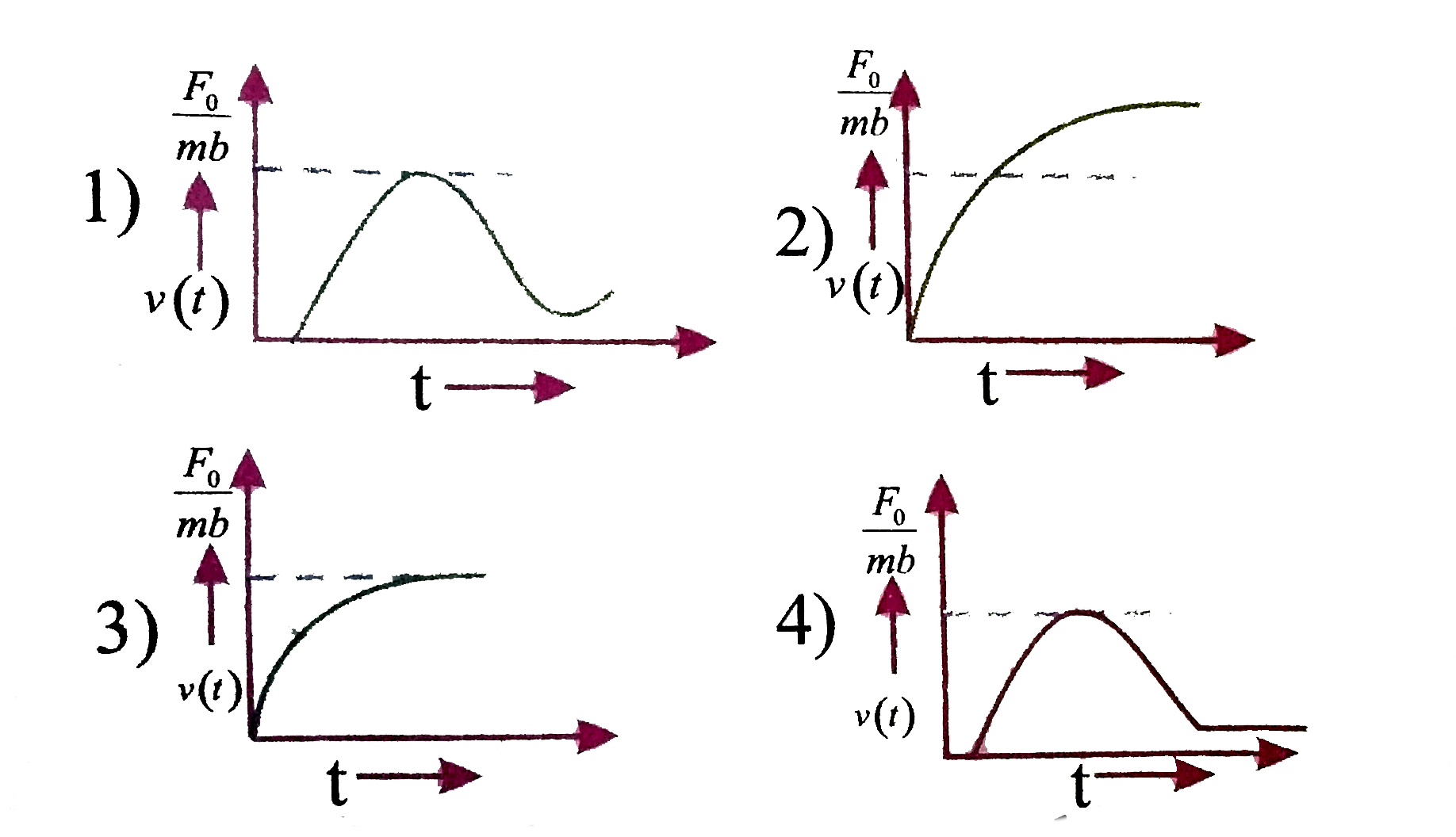
A particle of mass m is at rest the origin at time t=0 . It is subjected to a force F(t)=F0e−bt in the x - direction. Its speed v(t) is depicted by which of the following curves ?
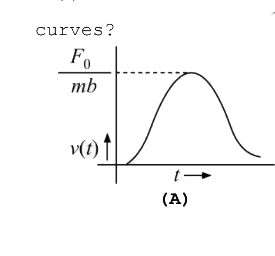
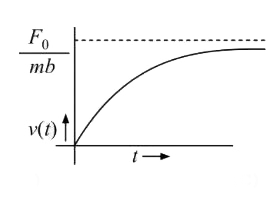
The correct Answer is:C
To solve the problem step by step, we will analyze the motion of a particle subjected to a time-dependent force.
Step 1: Identify the Force
The force acting on the particle is given by:
F(t)=F0e−bt
where F0 is a constant and b is a decay constant.
Step 2: Relate Force to Acceleration
According to Newton's second law, the force is related to mass and acceleration:
F=m⋅a
where a=dvdt (acceleration is the rate of change of velocity). Thus, we can write:
m⋅dvdt=F0e−bt
Step 3: Rearranging the Equation
Rearranging the equation gives:
dvdt=F0me−bt
Step 4: Integrate to Find Velocity
To find the velocity v(t), we need to integrate both sides with respect to time t:
∫dv=∫F0me−btdt
The left side integrates to v(t), and the right side can be integrated as follows:
v(t)=F0m∫e−btdt
The integral of e−bt is:
∫e−btdt=−1be−bt+C
where C is the constant of integration.
Step 5: Apply Initial Conditions
At t=0, the particle is at rest, so v(0)=0:
v(0)=F0m(−1be−b⋅0+C)=0
This simplifies to:
C=F0mb
Step 6: Final Expression for Velocity
Substituting C back into the equation for v(t):
v(t)=F0m(−1be−bt+F0mb)
This simplifies to:
v(t)=F0mb(1−e−bt)
Step 7: Analyze the Velocity Function
The velocity function v(t)=F0mb(1−e−bt) indicates that as t approaches infinity, e−bt approaches zero, and thus:
v(t)→F0mb
This means the velocity approaches a constant value as time increases.
Step 8: Sketch the Velocity Curve
The velocity starts from zero at t=0 and asymptotically approaches F0mb as t increases. The curve will be an increasing function that levels off, resembling an exponential growth curve.
Final Answer
The speed v(t) is depicted by a curve that starts at the origin (0,0) and approaches the horizontal asymptote F0mb as t increases.
---
The force acting on the particle is given by:
F(t)=F0e−bt
where F0 is a constant and b is a decay constant.
According to Newton's second law, the force is related to mass and acceleration:
F=m⋅a
where a=dvdt (acceleration is the rate of change of velocity). Thus, we can write:
m⋅dvdt=F0e−bt
Rearranging the equation gives:
dvdt=F0me−bt
To find the velocity v(t), we need to integrate both sides with respect to time t:
∫dv=∫F0me−btdt
v(t)=F0m∫e−btdt
∫e−btdt=−1be−bt+C
where C is the constant of integration.
At t=0, the particle is at rest, so v(0)=0:
v(0)=F0m(−1be−b⋅0+C)=0
This simplifies to:
C=F0mb
Substituting C back into the equation for v(t):
v(t)=F0m(−1be−bt+F0mb)
This simplifies to:
v(t)=F0mb(1−e−bt)
The velocity function v(t)=F0mb(1−e−bt) indicates that as t approaches infinity, e−bt approaches zero, and thus:
v(t)→F0mb
This means the velocity approaches a constant value as time increases.
The velocity starts from zero at t=0 and asymptotically approaches F0mb as t increases. The curve will be an increasing function that levels off, resembling an exponential growth curve.
The speed v(t) is depicted by a curve that starts at the origin (0,0) and approaches the horizontal asymptote F0mb as t increases.
Topper's Solved these Questions
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - JEE Advance (Archive) Level - II (SINGLE OPTION CORRECT TYPE )
31 Videos
- DYNAMICS OF A PARTICLEBOOK - VMC MODULES ENGLISHCHAPTER - DYNAMICS OF A PARTICLEEXERCISE - LEVEL 2 ( NUMERICAL TYPE FOR JEE MAIN )
16 Videos
- DC CIRCUITBOOK - VMC MODULES ENGLISHCHAPTER - DC CIRCUITEXERCISE - JEE ADVANCED ARCHIVE
68 Videos
- ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTBOOK - VMC MODULES ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTION & ALTERNATING CURRENTEXERCISE - IN-CHAPTER EXERCISE-G
10 Videos
Similar Questions
A particle of mass m is at rest at the origin at time t=0 It is subjected to a force F(t)=F0e−bt in the X-direction. Its speed V(t) is depicted by which of the following curves
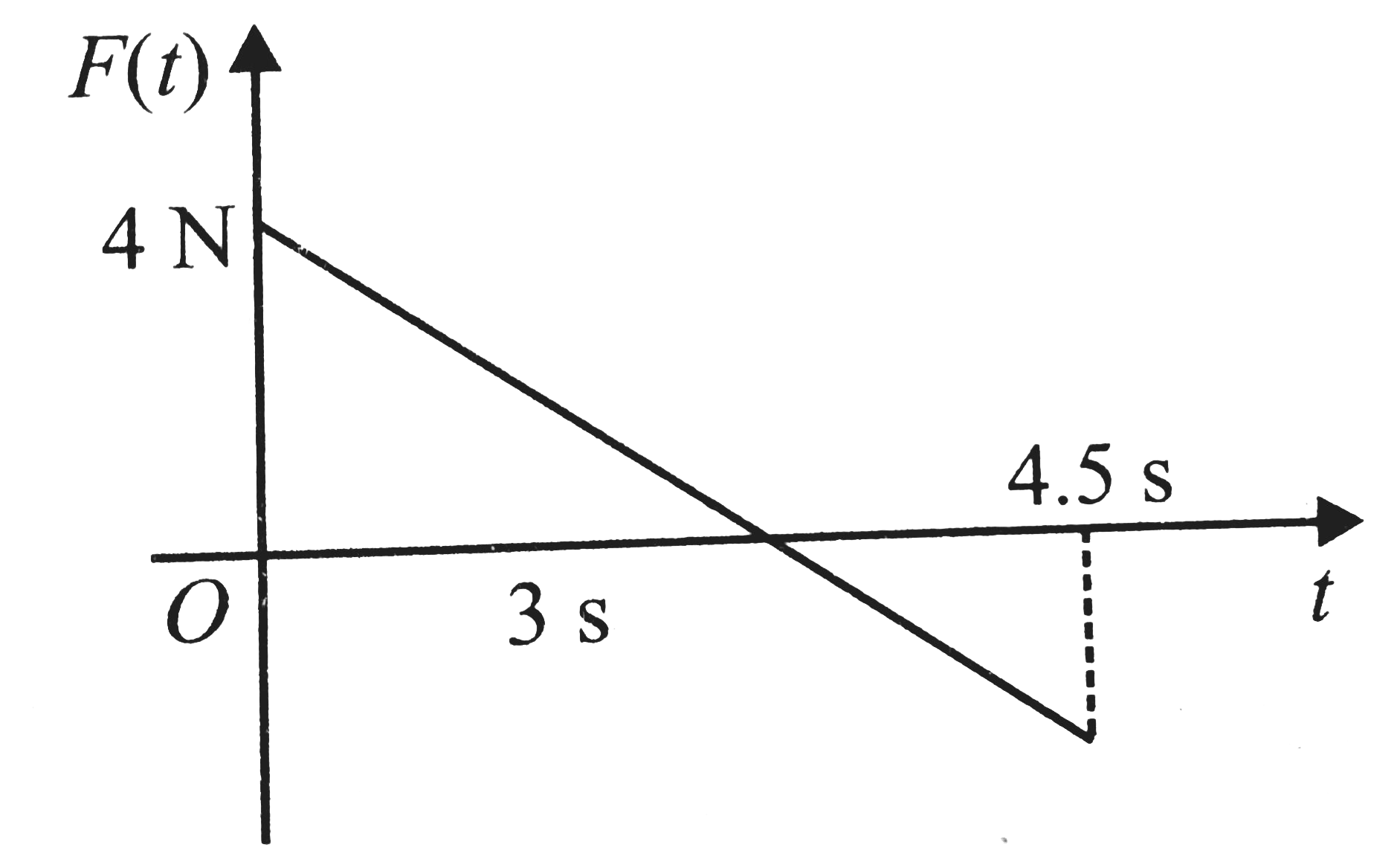
View SolutionA block of mass 2kg is free to move along the x-axis. It at rest and from t=0onwards it is subjected to a time-dependent force F(t) in the x direction. The force F(t) varies with t as shown in the figure. The kinetic energy of the block after 4.5 seconds is
View SolutionA particle of mass is moving in a straight line with momentum p. Starting at time t= 0, a force F= kt acts in the same direction on the moving particle during time interval T so that its momentum changes from p to 3p. Here k is constant . The value of T is :
View SolutionLet g(x)=∫ex0f'(t)dt1+t2. Which of the following is true?
View SolutionA particle of mass m is acted upon by a force F=t2−kx . Initially , the particle is at rest at the origin. Then
View SolutionA particle of mass 2 kg starts motion at time t = 0 under the action of variable force F = 4t (where F is in N and t is in s). The work done by this force in first two second is
View SolutionA particle is kept at rest at the origin. A constant force →F starts acting on it at t=0. Find the speed of the particle at time t.
View SolutionA particle of mass 0.1 kg is subjected to a force F which varies with distance x as shown. If it starts its journey from rest at x = 0, then its speed at X = 12 m is
View SolutionA particle moving on a curve has the position at time t given by x=f'(t)sint+f''(t)cost,y=f'(t)cost−f''(t)sint where f is a thrice differentiable function. Then prove that the velocity of the particle at time t is f'(t)+f'''(t).
View SolutionAcceleration of a particle is given by
a=3t2+2t+1
Where t is time . Find
(i) its velocity at time t assuming velocity to be 10 m/s at t = 0.
(ii) its position at time t assuming that the particle is at origin at t = 0.
(iii) What is the average speed of the particle in the duration t = 0 to t = 1s?
(iv) What is the average acceleration of the particle in the duration t = 0 to t = 1s?
View Solution
