The velocity of particle is v=v0+gt+ft2. If its position is x=0 at t=0 then its displacement after unit time (t=1) is
(a)v0+(g/2)+(f/3)
(b)v0+g+f
(c)v0+(g/2)+f
(d)v0+2g+3f
The correct Answer is:A
To solve the problem, we need to find the displacement of a particle after 1 second, given its velocity function and initial conditions. The velocity of the particle is given by:
v=v0+gt+ft2
Where:
- v0 is the initial velocity,
- g is the acceleration due to gravity,
- f is a constant,
- t is the time.
1. Understand the relationship between velocity and displacement:
Velocity is the rate of change of displacement with respect to time. Therefore, we can express displacement x as the integral of velocity over time.
x(t)=∫v(t)dt
2. Substitute the velocity function into the integral:
We substitute the given velocity function into the integral.
x(t)=∫(v0+gt+ft2)dt
3. Integrate the velocity function:
Now we perform the integration term by term.
x(t)=∫v0dt+∫gtdt+∫ft2dt
- The integral of v0 with respect to t is v0t.
- The integral of gt with respect to t is g2t2.
- The integral of ft2 with respect to t is f3t3.
Therefore, we have:
x(t)=v0t+g2t2+f3t3+C
Here, C is the constant of integration.
4. Apply the initial condition:
We know that at t=0, the position x=0. Therefore, we can find C:
x(0)=v0(0)+g2(0)2+f3(0)3+C=0
This implies C=0.
5. Final expression for displacement:
Thus, the displacement function simplifies to:
x(t)=v0t+g2t2+f3t3
6. Calculate displacement at t=1:
Now we substitute t=1 into the displacement equation:
x(1)=v0(1)+g2(1)2+f3(1)3
Simplifying this gives:
x(1)=v0+g2+f3
Final Answer:
The displacement after 1 second is:
x(1)=v0+g2+f3
- v0 is the initial velocity,
- g is the acceleration due to gravity,
- f is a constant,
- t is the time.
Velocity is the rate of change of displacement with respect to time. Therefore, we can express displacement x as the integral of velocity over time.
We substitute the given velocity function into the integral.
Now we perform the integration term by term.
- The integral of gt with respect to t is g2t2.
- The integral of ft2 with respect to t is f3t3.
We know that at t=0, the position x=0. Therefore, we can find C:
Thus, the displacement function simplifies to:
Now we substitute t=1 into the displacement equation:
The displacement after 1 second is:
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - JEE Advanced (archive)
14 Videos
- KINEMATICS OF A PARTICLE BOOK - VMC MODULES ENGLISHCHAPTER - KINEMATICS OF A PARTICLE EXERCISE - LEVEL 2
65 Videos
- JEE MAIN REVISON TEST-23BOOK - VMC MODULES ENGLISHCHAPTER - JEE MAIN REVISON TEST-23EXERCISE - PHYSICS (SECTION 2)
1 Video
- LAWS OF MOTION BOOK - VMC MODULES ENGLISHCHAPTER - LAWS OF MOTION EXERCISE - IMPECCABLE
53 Videos
Similar Questions
Velocity of a particle varies with time as v=4t. Calculate the displacement of particle between t=2 to t=4 sec.
View SolutionVelocity-time equation of a particle moving in a straight line is, v=(10+2t+3t2) (SI units) Find
(a) displacement of particle from the mean position at time t=1s, if it is given that displacement is 20m at time t=0.
(b) acceleration-time equation.
View SolutionVx is the velocity of a particle of a particle moving along the x−axis as shown. If x=2.0m at t=1.0s, what is the position of the particle at t=6.0s?

View SolutionVelocity of a particle moving in a straight line varies with its displacement as v=(√4+4s)m/s. Displacement of particle at time t=0 is s=0. Find displacement of particle at time t=2s.
View SolutionThe intial velocity of a particle moving along x axis is u (at t = 0 and x = 0) and its acceleration a is given by a = kx. Which of the following equation is correct between its velocity (v) and position (x)?
View SolutionFor a particle displacement time relation is t=√x+3. Its displacement when its velocity is zero -
View SolutionIf velocity of particle is given by v=2t4, then its acceleration (dvdt) at any time t will be given by..
View SolutionThe velocity 'v' of a particle moving along straight line is given in terms of time t as v=3(t2−t) where t is in seconds and v is in m/s.
The displacement of aprticle from t=0 to t=2 seconds is :
View SolutionThe position of a particle along X-axis at time t is given by x=2+t−3t2. The displacement and the distance travelled in the interval, t = 0 to t = 1 are respectively
View SolutionThe velocity (v)-time (t) graph of a partide moving along a straight line is as shown in the figure. The displacement of the particle from t = 0 to t = 4 is
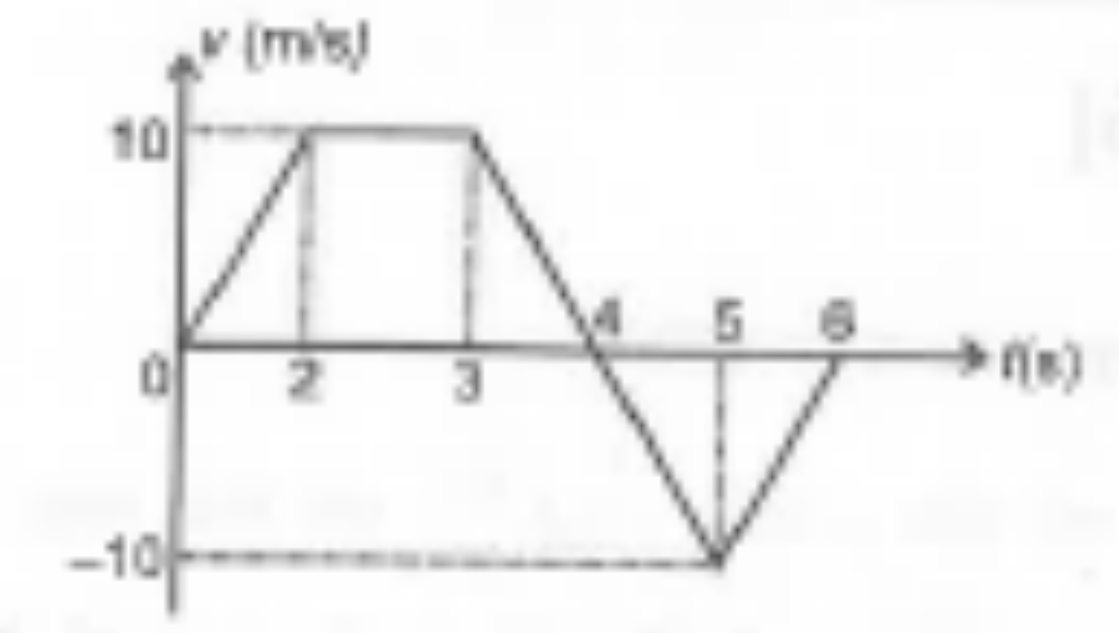
View Solution
