Speeds of two identical cars are u and 4u at at specific instant. The ratio of the respective distances in which the two cars are stopped from that instant is
1:1
1:4
1:8
1:16
The correct Answer is:D
To solve the problem of finding the ratio of the distances in which two identical cars stop, given their speeds u and 4u, we can follow these steps:
Step 1: Understand the Problem
We have two identical cars. Car A is moving with speed u and Car B is moving with speed 4u. Both cars will apply brakes and come to a stop. We need to find the ratio of the distances s1 (for Car A) and s2 (for Car B) that they travel before stopping.
Step 2: Use the Kinematic Equation
We will use the third kinematic equation which relates initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
Where:
- v = final velocity (0 when the car stops)
- u = initial velocity
- a = acceleration (negative in this case as it is retardation)
- s = distance traveled before stopping
Step 3: Set Up the Equations
For Car A (speed u):
0=u2+2(−a)s1⇒u2=2as1⇒s1=u22a
For Car B (speed 4u):
0=(4u)2+2(−a)s2⇒16u2=2as2⇒s2=16u22a=8u2a
Step 4: Find the Ratio of Distances
Now we can find the ratio s1s2:
s1s2=u22a8u2a=u22a⋅a8u2=116
Conclusion
Thus, the ratio of the distances in which the two cars stop is:
s1s2=116
We have two identical cars. Car A is moving with speed u and Car B is moving with speed 4u. Both cars will apply brakes and come to a stop. We need to find the ratio of the distances s1 (for Car A) and s2 (for Car B) that they travel before stopping.
We will use the third kinematic equation which relates initial velocity, final velocity, acceleration, and distance:
v2=u2+2as
Where:
- v = final velocity (0 when the car stops)
- u = initial velocity
- a = acceleration (negative in this case as it is retardation)
- s = distance traveled before stopping
For Car A (speed u):
0=u2+2(−a)s1⇒u2=2as1⇒s1=u22a
0=(4u)2+2(−a)s2⇒16u2=2as2⇒s2=16u22a=8u2a
Now we can find the ratio s1s2:
s1s2=u22a8u2a=u22a⋅a8u2=116
Thus, the ratio of the distances in which the two cars stop is:
s1s2=116
Topper's Solved these Questions
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:JEE Advanced (archive)
Explore 14 Videos
- KINEMATICS OF A PARTICLE Book:VMC MODULES ENGLISHChapter:KINEMATICS OF A PARTICLE Exercise:LEVEL 2
Explore 65 Videos
- JEE MAIN REVISON TEST-23Book:VMC MODULES ENGLISHChapter:JEE MAIN REVISON TEST-23Exercise:PHYSICS (SECTION 2)
Explore 1 Video
- LAWS OF MOTION Book:VMC MODULES ENGLISHChapter:LAWS OF MOTION Exercise:IMPECCABLE
Explore 53 Videos
Similar Questions
A car is moving along a straight horizontal road with a speed v0 . If the coefficient of friction between the tyres and the road is μ , the shortest distance in which the car can be stopped is
View SolutionTwo particle are moing along X and Y axes towards the origin with constant speeds u and v respectively. At time t=0, their repective distance from the origin are x and y. The time instant at which the particles will be closest to each other is
View Solution
Knowledge Check
A car can be stopped within a distance of s when its speed is v. What is the minimum distance within which the car can be stopped during the same time when its speed is nv ?
AnsBs/nCn2sDs/n2
Two racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.
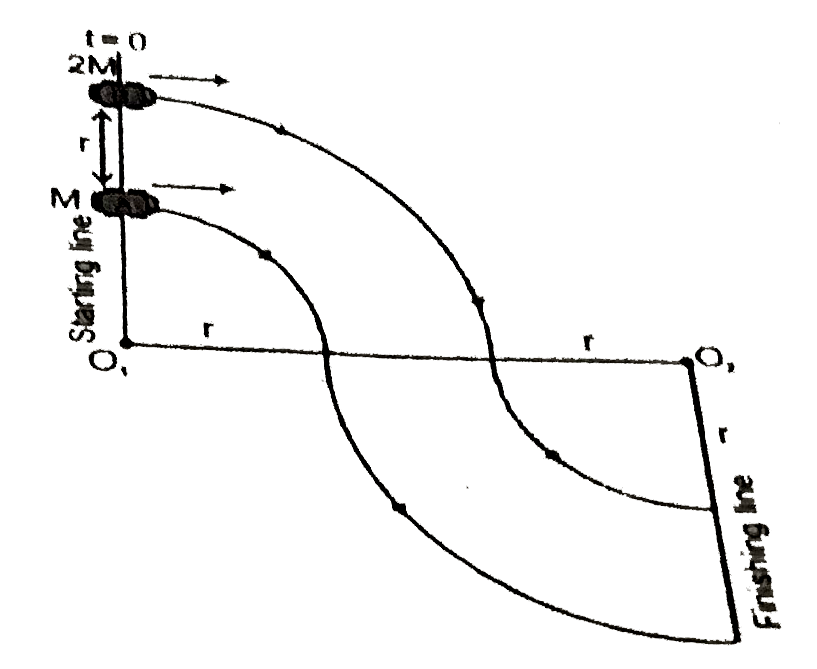
The time interval during which the two cars have same angular speed :
View SolutionTwo racing cars 'A' and 'B' having masses 'M' and '2m' respectively start running from the starting line on a horizontal plane.Both cars 'A' and B' have same speed 'V' which is constant through out the journey. The track of the two cars are the arcs of concentric circle having centres O1 and O2 as shwon in figure with data. The friction coefficient of the two cars with the road is same. There is a finishing line at the end of the arc. Using these informations solve the following questions.

Which of the following statements is incorrect.
View SolutionThe driver of a car moving with a speed of 10ms−1 sees a red light ahead, applies brakes and stops after covering 10 m distance. If the same car were moving with a speed of 20ms−1 the same driver would have stopped the car after covering 30 m distance. Within what distance the car can be stopped if traveling with a velocity of 15ms−1 Assume the same reaction time and the same deceleration in each case
View SolutionA straight highway leads to the foot of a tower of height 50 m. From the top of the tower, the angles of depression of two cars standing on the highway are 30∘ and 60∘ respectively. What is the distance between the two cars and how far is each car from the tower?
View SolutionA driver having a definite reaction time is capable of stopping his car over a distance of 30 m on seeing a red traffic signal, when the speed of the car is 72 km/hr andover a distance of 10 m when the speed is 36 km/hr. Find the distance over which he can stop the car if it were running at a speed of 54 km/hr. Assume that his reaction time and the deceleration of the car remains same in all the three cases.
View SolutionWhen the speed of a car is u, the mimimum distance over which it canbe stopped is a, If speed becomes ν, what will be the mimimum distance over which it can be stopped during the same time?
View SolutionA car is moving towards south with a speed of 20ms−1. A motorcycst is moving towards east with a speed of 15ms−1. At a crttain instant, the motorcyclistis due south of the car and is at a distance of 50mfrom the car.
The shortest distance between the motorcyclist and the car is.
View Solution

